Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
Halloween night was rainy, so many fewer kids knocked on the door than usual. Consequently, I'm left with a big bucket of undistributed candy. One evening as I treated myself to a mouthful of tooth decay, I chanced to open a package of Wonka® Bottle Caps. The package contained three
Did you know that you can define "abbreviations" in the SAS enhanced editor? These handy little shortcuts can save you a lot of typing. For example, I have an abbreviation for the string _iml. Whenever I type _iml, the editor prompts me to replace those four characters with the following
Here is a little trick to file away. Given a row vector of zeros and ones, thought of as representing a number in base 2, the following SAS/IML statements compute the decimal value of that vector. proc iml; x = {1 0 0 1 1 1}; /* number in base
One aspect of blogging that I enjoy is getting feedback from readers. Usually I get statistical or programming questions, but every so often I receive a comment from someone who stumbled across a blog post by way of an internet search. This morning I received the following delightful comment on
If you want to extract values from a SAS/IML vector, use the subscripting operation, such as in the following example: proc iml; x = {A B C D E}; y = x[{1 2 3}]; /* {A,B,C} */ The vector y contains the first three elements of x. However, did you
Sometimes you want to label only certain observations in a plot. This is useful in many ways, but one use is to label outliers on a scatter plot. In the SGPLOT procedure, the DATALABEL= option enables you to specify the name of a variable that is used to label observations.
I was at the Wikipedia site the other day, looking up properties of the Chi-square distribution. I noticed that the formula for the median of the chi-square distribution with d degrees of freedom is given as ≈ d(1-2/(9d))3. However, there is no mention of how well this formula approximates the
What do you call an interview on Twitter? A Tw-interview? A Twitter-view? Regardless of what you call it, I'm going to be involved in a "live chat" on Twitter this coming Thursday, 10NOV2011, 1:30–2:00pm ET. The hashtag is #saspress. Shelly Goodin (@SASPublishing) and SAS Press author recruiter Shelley Sessoms (@SSessoms)
Last week I showed how to use the UNIQUE-LOC technique to iterate over categories in a SAS/IML program. The observant reader might have noticed that the algorithm, although general, could be made more efficient if the data are sorted by categories. The UNIQUEBY Technique Suppose that you want to compute
Being able to reshape data is a useful skill in data analysis. Most of the time you can use the TRANSPOSE procedure or the SAS DATA step to reshape your data. But the SAS/IML language can be handy, too. I only use PROC TRANSPOSE a few times per year, so
I was recently asked the following question: I am using bootstrap simulations to compute critical values for a statistical test. Suppose I have test statistic for which I want a p-value. How do I compute this? The answer to this question doesn't require knowing anything about bootstrap methods. An equivalent
When you analyze data, you will occasionally have to deal with categorical variables. The typical situation is that you want to repeat an analysis or computation for each level (category) of a categorical variable. For example, you might want to analyze males separately from females. Unlike most other SAS procedures,
In SAS/IML 9.22 and beyond, you can call the R statistical programming language from within a SAS/IML program. The syntax is similar to the syntax for calling SAS from SAS/IML: You use a SUBMIT statement, but add the R option: SUBMIT / R. All statements in the program between the
"I think that my data are exponentially distributed, but how can I check?" I get asked that question a lot. Well, not specifically that question. Sometimes the question is about the normal, lognormal, or gamma distribution. A related question is "Which distribution does my data have," which was recently discussed
I was contacted by SAS Technical Support regarding a customer who was trying to use SAS/IML to compute quantiles of the folded normal distribution. I had heard of the distribution, but it is not built into SAS and I had never worked with it. Nevertheless, I set out to understand
In SAS/IML 9.22 and beyond, you can call any SAS procedure, DATA step, or macro from within a SAS/IML program. The syntax is simple: place a SUBMIT statement prior to the SAS statements and place an ENDSUBMIT statement after the SAS statements. This enables you to call any SAS procedure
When I learn a new statistical technique, one of first things I do is to understand the limitations of the technique. This blog post shares some thoughts on modeling finite mixture models with the FMM procedure. What is a reasonable task for FMM? When are you asking too much? I
Normal, Poisson, exponential—these and other "named" distributions are used daily by statisticians for modeling and analysis. There are four operations that are used often when you work with statistical distributions. In SAS software, the operations are available by using the following four functions, which are essential for every statistical programmer
I received the following email: Dear Dr. Wicklin, Why doesn't SYMPUT work in IML? In the DATA step, I can say CALL SYMPUT("MyMacro", 5) but this doesn't work in IML! Frustrated Dear Frustrated, The SYMPUT subroutine does work in SAS/IML software! However, the second argument to SYMPUT must be a
I previously wrote about using SAS/IML for nonlinear optimization, and demonstrated optimization by maximizing a likelihood function. Many well-known optimization algorithms require derivative information during the optimization, including the conjugate gradient method (implemented in the NLPCG subroutine) and the Newton-Raphson method (implemented in the NLPNRA method). You should specify analytic
A popular use of SAS/IML software is to optimize functions of several variables. One statistical application of optimization is estimating parameters that optimize the maximum likelihood function. This post gives a simple example for maximum likelihood estimation (MLE): fitting a parametric density estimate to data. Which density curve fits the
To celebrate the first anniversary of Statistical Programming with SAS/IML Software, you can now download the SAS/IML tip sheets (also called "cheat sheets") that I created for the book. At conferences, SAS Press displays these tip sheets next to my book. They have been very popular. Download these SAS/IML cheat
I've noticed that a lot of people want to be able to draw bar charts with confidence intervals. This topic is a frequent posting on the SAS/GRAPH and ODS Graphics Discussion Forum and on the SAS-L mailing list. Consequently, this post describes how to add errors bars to a bar
When you misspell a word on your mobile device or in a word-processing program, the software might "autocorrect" your mistake. This can lead to some funny mistakes, such as the following: I hate Twitter's autocorrect, although changing "extreme couponing" to "extreme coupling" did make THAT tweet more interesting. [@AnnMariaStat] When
SAS has several ways to round a number to an integer. You can round a number up, round it down, or round it to the nearest integer. If your data contain both positive and negative values, you can also round numbers toward zero, or away from zero. The functions that
Birds migrate south in the fall. Squirrels gather nuts. Humans also have behavioral rituals in the autumn. I change the batteries in my smoke detectors, I switch my clocks back to daylight standard time, and I turn the mattress on my bed. The first two are relatively easy. There's even
I previously wrote about an intriguing math puzzle that involves 5-digit numbers with certain properties. This post presents my solution in the SAS/IML language. It is easy to generate all 5-digit perfect squares, but the remainder of the problem involves looking at the digits of the squares. For this reason,
A few sharp-eyed readers questioned the validity of a technique that I used to demonstrate two ways to solve linear systems of equations. I generated a random n x n matrix and then proceeded to invert it, seemingly without worrying about whether the matrix even has an inverse! I responded to the
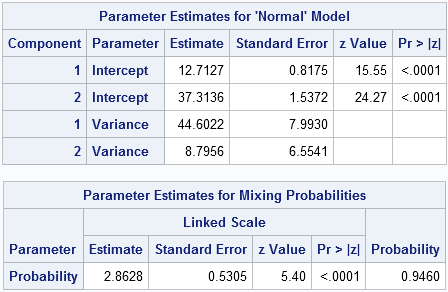
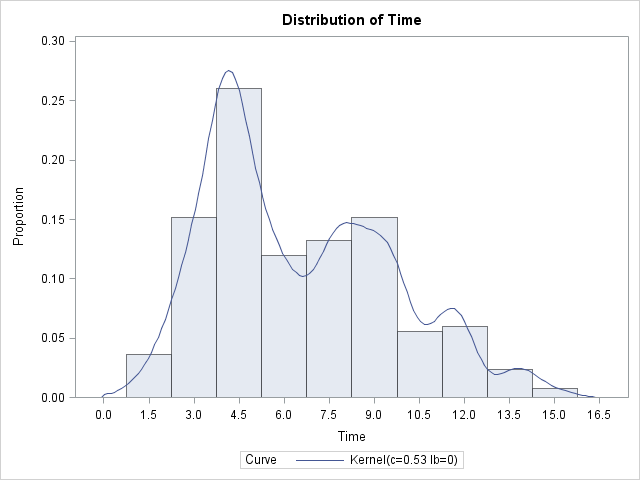
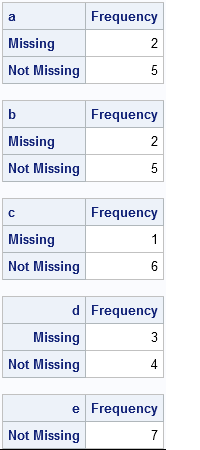
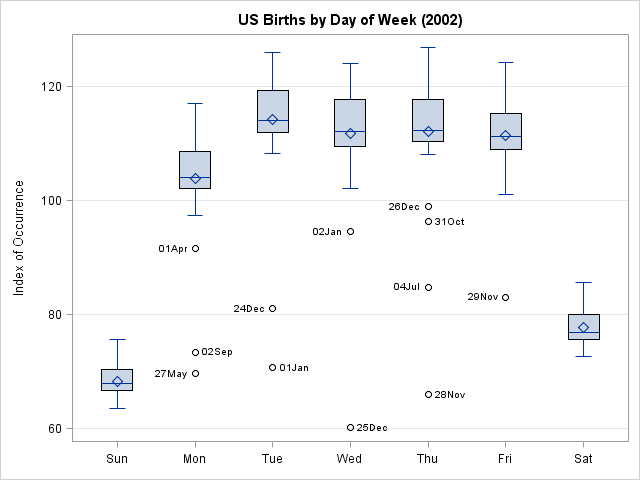
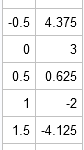
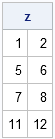
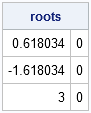
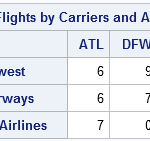
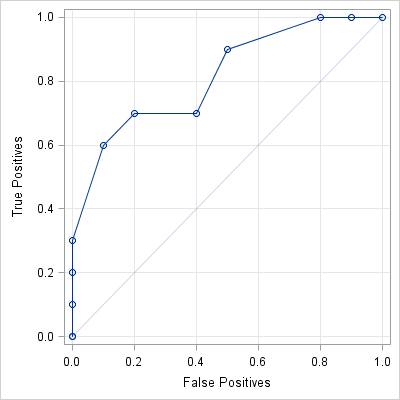
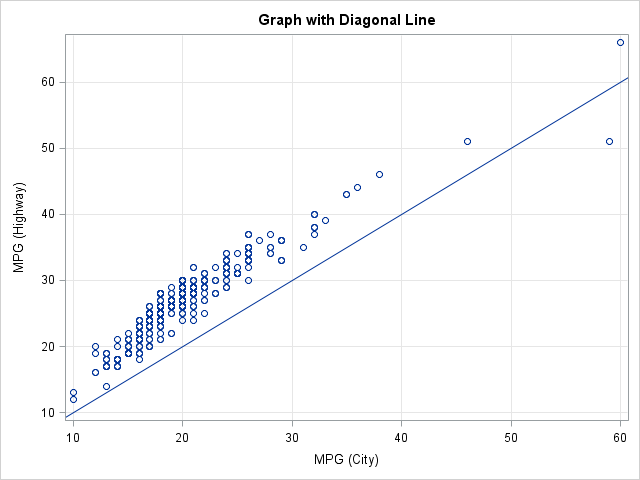
I was intrigued by a math puzzle posted to the SAS Discussion Forum (from New Scientist magazine). The problem is repeated below, but I have added numbers in brackets because I am going to comment on each clue: [1] I have written down three different 5-digit perfect squares, which [2]
I showed a SAS/IML customer a debugging tip, and she said that I should blog about it because she had never seen it before. The tip is very simple: inside of a DO loop, use the MOD function to selectively print the values of variables. Recall that the expression MOD(a,b)
