Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
This article describes the SAS/IML CHOOSE function: how it works, how it doesn't work, and how to use it to make your SAS/IML programs more compact. In particular, the CHOOSE function has a potential "gotcha!" that you need to understand if you want your program to perform as expected. What
When I was at the Joint Statistical Meetings (JSM) last week, a SAS customer asked me whether it was possible to use the SGPLOT procedure to produce side-by-side bar charts. The answer is "yes" in SAS 9.3, thanks to the new GROUPDISPLAY= option on the VBAR and HBAR statements. For
The SAS/IML language provides two functions for solving a nonsingular nxn linear system A*x = c: The INV function numerically computes the inverse matrix, A-1. You can use this to solve for x: Ainv = inv(A); x = Ainv*c;. The SOLVE function numerically computes the particular solution, x, for a
In the SAS/IML language, the index creation operator (:) is used to construct a sequence of integer values. For example, the expression 1:7 creates a row vector with seven elements: 1, 2, ..., 7. It is important to know the precedence of matrix operators. When I was in grade school,
I've previously discussed how to find the root of a univariate function. This article describes how to find the root (zero) of a function of several variables by using Newton's method. There have been many papers, books, and dissertations written on the topic of root-finding, so why am I blogging
At the SAS/IML Support Community, a SAS/IML programmer recently asked how to find "the root of a complicated equation." That's a huge question, and many papers and books have been written on the topic of root-finding, also known as finding the zeros of a function. Everyone has favorite techniques for
A matrix is an array of numbers or character strings. When I print a matrix, I usually want to see only the data. However, sometimes it is helpful to add row or column headings that indicate the names of variables or labels for rows. A simple example is count data
In a previous blog post, I showed how to use the LOGISTIC procedure to construct a receiver operator characteristic (ROC) curve in SAS. That same day, Charlie H. blogged about how to use the DATA step to construct an ROC curve from basic principles. It has been a long time
I've written about how to add a diagonal line to a scatter plot by using the SGPLOT procedure in SAS 9.2. The main idea (use the VECTOR statement) is easy enough, but writing a program that handles a line with any slope requires some additional effort. But now SAS 9.3
The other day I needed to compute the signum function for each element of a matrix. If x is a real number, then the sgn(x) is -1 when x<0, 1 when x>0, and 0 when x=0. I wrote a SAS/IML module that contains a compact little expression: proc iml; start
I recently blogged about how many times, on average, you must roll a die until you see all six faces. This question is a special case of the coupon collector's problem. My son noted that the expected value (the mean number of rolls) is not necessarily the best statistic to
"Dad? How many times do I have to roll a die until all six sides appear?" I stopped what I was doing to consider my son's question. Although I could figure out the answer mathematically, sometimes experiments are more powerful than math equations for showing how probability works. "Why don't
Yesterday, Jiangtang Hu did a frequency analysis of my blog posts and noticed that there are some holidays on which I post to my blog and others on which I do not. The explanation is simple: I post on Mondays, Wednesdays, and Fridays, provided that SAS Institute (World Headquarters) is
Dates and times. As Wayne Finley states in his SUGI25 paper on SAS date and time handling, "The SAS system provides a plethora of methods to handle date and time values." Along with the plethora of methods is a plethora of papers on the topic. If you want to trick
Welcome, SAS 9.3! I've already blogged about some interface and graphical changes that everyone should know about. Now I'll put on my statistical hat and mention a few 9.3 features that excite me, personally, as a data analyst and a statistical programmer: As a statistician, I am keen to try
Here are a few new interface and graphics changes that every SAS programmer should know about SAS 9.3: HTML is now the default output destination when you run the SAS windowing environment. This means that tables and graphs appear in an HTML document instead of the classic LISTING destination. Of
As I was reviewing notes for my course "Data Simulation for Evaluating Statistical Methods in SAS," I realized that I haven't blogged about simulating categorical data in SAS. This article corrects that oversight. An Easy Way and a Harder Way SAS software makes it easy to sample from discrete "named"
Arnold Loewy, professor of criminal law at Texas Tech University, wrote an editorial about the Casey Anthony case that has statistical undertones. Prof. Loewy discusses the fact that there are two kinds of errors that can occur in a court trial: an innocent person can be sent to jail or
"Always clean up after yourself." My mother taught me this, and I apply it to SAS programming as regularly as I apply it at home. For SAS programming, I reinterpret Mom's saying as the following rule: Always delete temporary files and data sets when you are finished using them. How
One of the joys of statistics is that you can often use different methods to estimate the same quantity. Last week I described how to compute a parametric density estimate for univariate data, and use the parameters estimates to compute the area under the probability density function (PDF). This article
If you create a scatter plot of highly correlated data, you will see little more than a thin cloud of points. Small-scale relationships in the data might be masked by the correlation. For example, Luke Miller recently posted a scatter plot that compares the body temperature of snails when they
In a previous article, I discussed random jittering as a technique to reduce overplotting in scatter plots. The example used data that are rounded to the nearest unit, although the idea applies equally well to ordinal data in general. The act of jittering (adding random noise to data) is a
Jittering. To a statistician, it is more than what happens when you drink too much coffee. Jittering is the act of adding random noise to data in order to prevent overplotting in statistical graphs. Overplotting can occur when a continuous measurement is rounded to some convenient unit. This has the
The area under a density estimate curve gives information about the probability that an event occurs. The simplest density estimate is a histogram, and last week I described a few ways to compute empirical estimates of probabilities from histograms and from the data themselves, including how to construct the empirical
In my statistical analysis of coupons article, I presented a scatter plot that includes the identity line, y=x. This post describes how to write a general program that uses the SGPLOT procedure in SAS 9.2. By a "general program," I mean that the program produces the result based on the
In Base SAS you can use the DATASETS procedure to determine the SAS data sets in a library, and you can use the DELETE statement to delete data sets. Did you know that you can do the same operations from within the SAS/IML language? The following DATA step creates four
Readers' comments indicate that my previous blog article about computing the area under an ROC curve was helpful. Great! There is another common application of numerical integration: finding the area under a density estimation curve. This article provides an overview of density estimation and computes an empirical cumulative density function.
This is Part 4 of my response to Charlie Huang's interesting article titled Top 10 most powerful functions for PROC SQL. As I did for eaerlier topics, I will examine one of the "powerful" SQL functions that Charlie mentions and show how to do the same computation in SAS/IML software.
A reader commented to me that he wants to use the HISTOGRAM statement of the SGPLOT procedure to overlay two histograms on a single plot. He could do it, but unfortunately SAS was choosing a large bin width for one of the variables and a small bin width for the
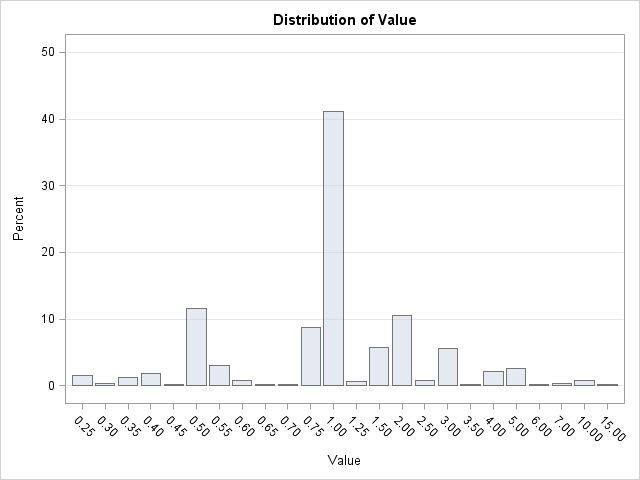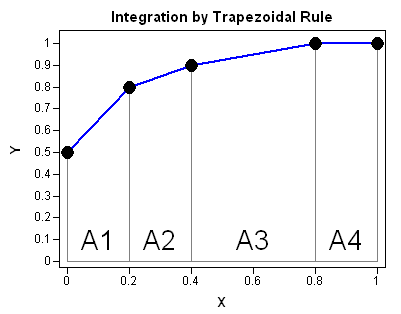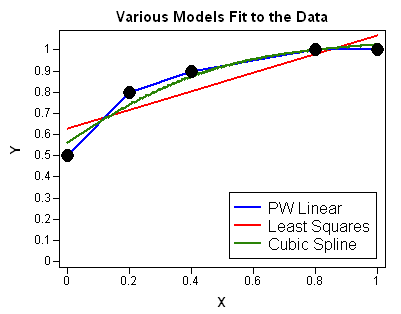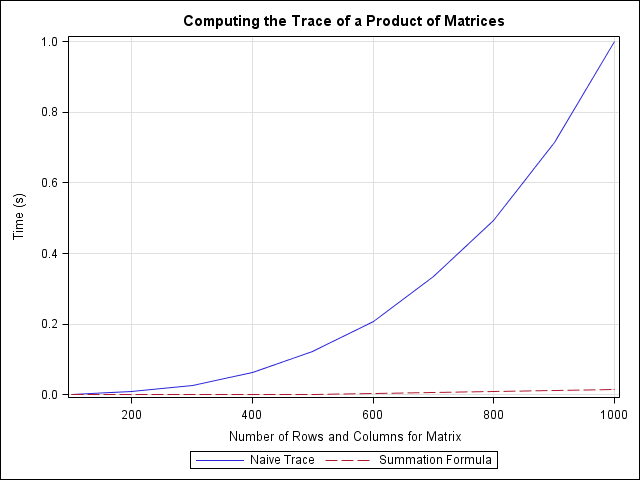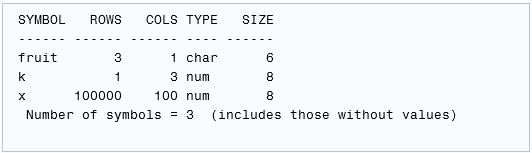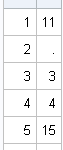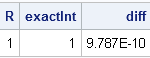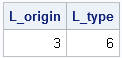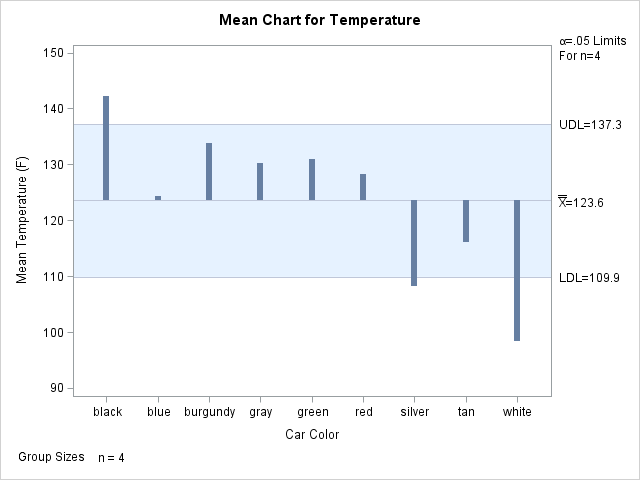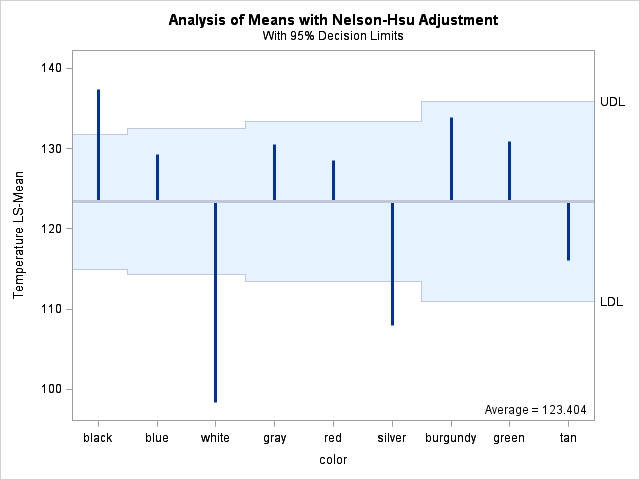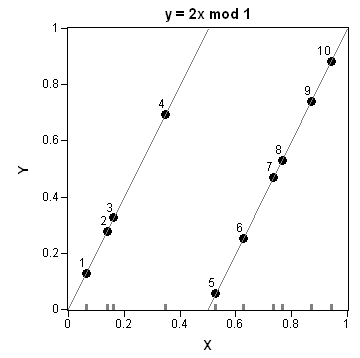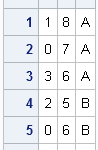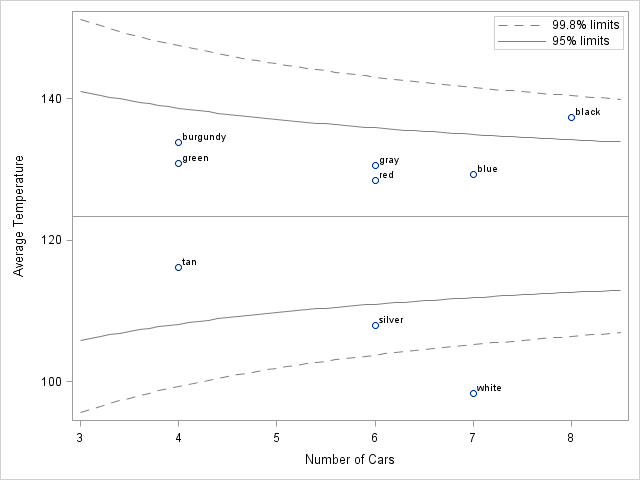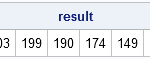
Recently Charlie Huang showed how to use the SAS/IML language to compute an exponentially weighted moving average of some financial data. In the commentary to his analysis, he said: I found that if a matrix or a vector is declared with specified size before the computation step, the program’s efficiency
