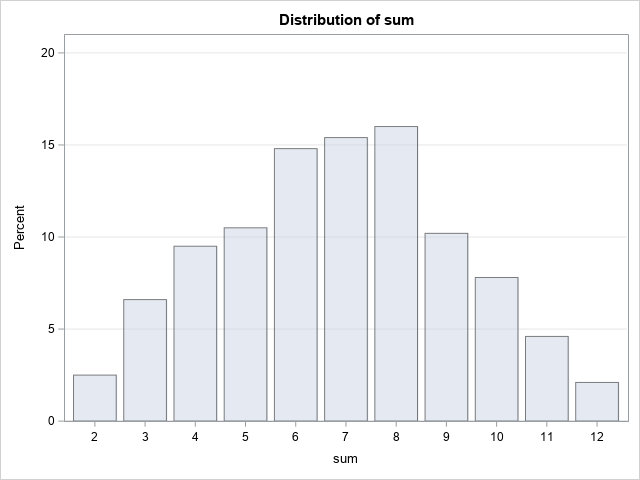
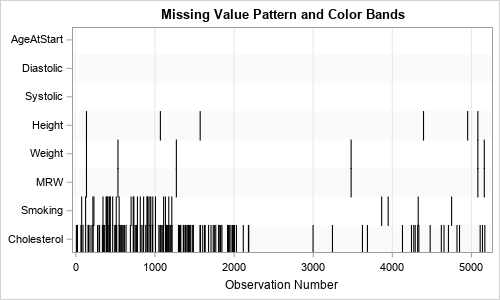
Strengthen your programming skills with tips and techniques from the experts
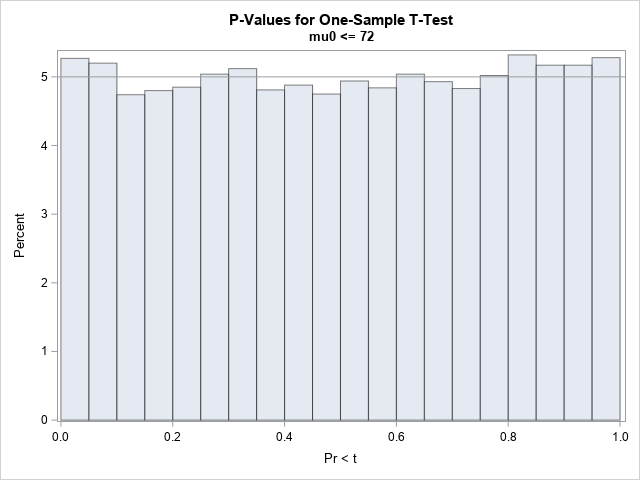
A SAS statistical programmer recently asked a theoretical question about statistics. "I've read that 'p-values are uniformly distributed under the null hypothesis,'" he began, "but what does that mean in practice? Is it important?" I think data simulation is a great way to discuss the conditions for which p-values are