All Posts

At SAS Innovate in Las Vegas, attendees should be excited for many reasons. From inspiring keynote speakers to breakout sessions sure to teach you something new and more, this event will have something for everyone to enjoy. Just take the SAS Innovation Hub for example. This interactive space is the

Growing up involves a long process of discovering more about ourselves and the world around us. Looking back at our younger selves' decisions and thought processes can leave a sense of laughter, embarrassment, growth or even pride. Thinking about how far you’ve come as a person can be rewarding. For

Aqui o ambiente é extremamente saudável, eu me sinto desafiada o tempo inteiro. Mas é aquele desafio bom em que você se sente segura, e a liderança está sempre aberta a te ouvir. Destaque do mês de março na série Orgulho de Ser SAS, Mariana Nogueira é formada em relações

Consultoras como McKinsey calculan que IAG podría agregar entre 2.6 y 4.4 billones de dólares a la economía global, mientras que IDC señala que es tal la acogida de este tipo de soluciones que el gasto de las empresas por ellas ya se acercó a los 20 mil millones de

En un contexto de cambios acelerados, el Banco Popular, una de las instituciones bancarias líderes en Colombia, ha demostrado que los tiempos de mayores retos pueden convertirse en oportunidades de transformación. Durante los desafíos de la pandemia, el banco se propuso llevar su estrategia de gestión de riesgo crediticio a

Data quality is a cornerstone for integrating large language models (LLMs) into organizations. The adage "garbage in, garbage out" holds particularly true here. High-quality data is the lifeblood that ensures the accuracy, relevance, and reliability of the model's outputs. In a business context, this translates to insights and decisions that

There’s something about the air fryer that makes food more cravable. If you have the space to leave an air fryer out on the countertop, chances are you’ll use it all the time. Here are a few of my favorite convenient ways to use mine.

A customer’s onboarding journey is often the most interaction they will have with their bank. Onboarding activities provide the first meaningful insights into what being a customer will be like, and they can make or break the long-term prospects of the relationship. Unfortunately, the onboarding journey at many banks is

À medida em que as organizações avançam suas estratégias digitais, a necessidade de entender profundamente os seus clientes se torna cada vez mais evidente. E é aqui que a plataforma de dados do cliente, também conhecida como Customer Data Platform (CDP), desempenha um papel fundamental. Neste artigo, detalho o conceito

At the end of the Indiana Jones classic Raiders of the Lost Ark, an older man struggles to push a cart carrying a large wooden box down a warehouse hallway. This iconic scene takes place in an enormous space filled with other large wooden boxes stacked to the sky. The

While large language models (LLMs) have become synonymous with advanced AI capabilities, their integration into various business and technological domains is often accompanied by significant costs. These costs arise from the extensive computational resources required for training and running these models. However, traditional natural language processing (NLP) techniques offer a

SAS' Julia Florou-Moreno shows you how to use generative AI to build a digital assistant that interacts with a model using natural language conversation.
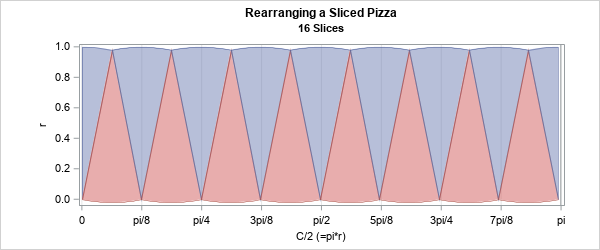
Happy Pi Day! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate all things pi-related because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979.... Pi is a mathematical constant defined as the ratio of a circle's circumference (C) to its diameter (D).

Best-selling author and banking industry futurist Brett King once said, “The easiest customer experience isn’t one where you drive to the branch, find a parking spot, wait in line, ask advice, and sign a piece of paper. It’s one where you activate the service you need in real time when

Making a difference involves taking meaningful actions that contribute positively to society. Whether it's through volunteering, creating innovative solutions or advocating for important causes, each action advances change. This is the third post in a new series highlighting women from diverse backgrounds as they share their experiences in the tech










