Graphically Speaking
Data Visualization with a focus on SAS ODS Graphics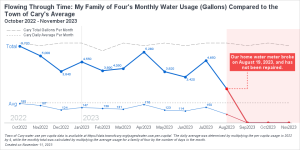
Have you ever been curious about your monthly water consumption and how it compares to others in your community? Recently, I had this question and decided to get ahold of my family's water usage data for analysis. Harnessing the power of data visualization, I compared my family of four's monthly
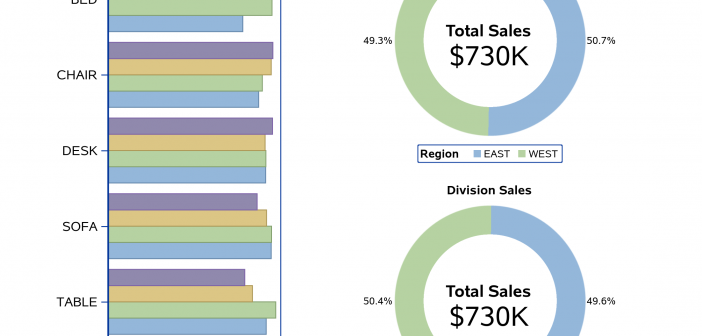
The Graph Template Language (GTL) is a powerful tool for creating a wide range of graphic displays. One feature GTL has is the ability to combine independent plots together into one paneled display. The SG procedures have some limited capabilities in this area; but in this post, I am going
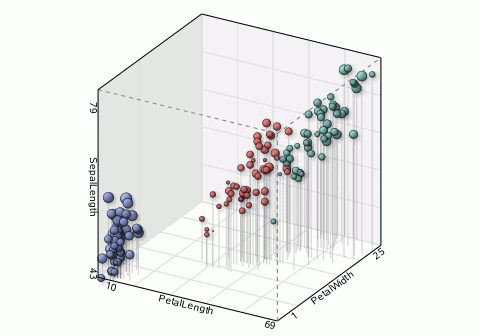
SAS SGPLOT already provides the necessary graphical elements for complex visualization. 3D or high-dimensional data can be easily visualized after being projected appropriately. With SAS' strong support for animation features, SAS users can create complicated 3D or high dimension visualizations quickly.
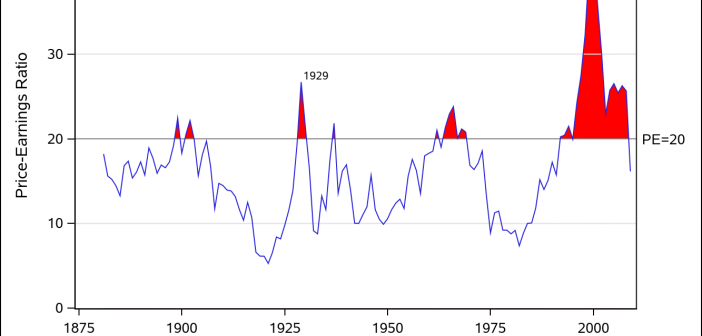
Amazing things can be created when you start with small pieces and stack them together. Just ask Bryan Berg. He is the current world record holder for the tallest house of cards. This same principle can be applied to the SGPLOT and SGPANEL procedures. You can take the individual plot
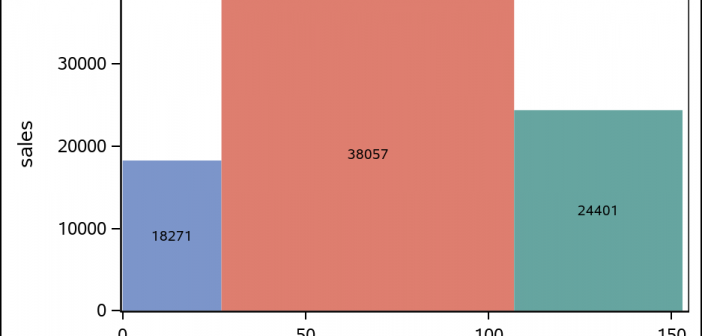
The SGPLOT procedure supports a wide variety of plot types that you can use directly or combine together to create more complex graphs. Even with this flexibility, there might be times you run across a graph that you cannot create using one of the standard plot types. An "area" bar
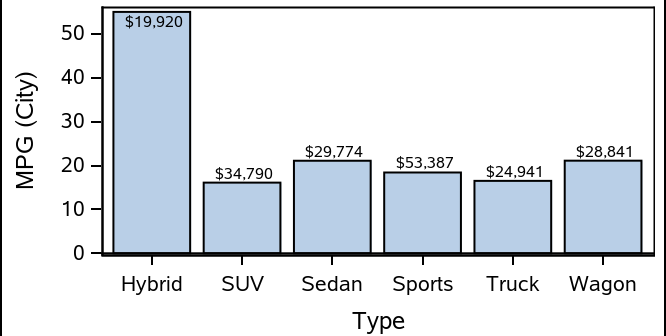
When creating bar charts, it is very common to display labels with the bars to make it easier to determine the bar values or to provide additional information in the chart. However, these labels can take away valuable data space, particularly if you generate a smaller-sized graph. As you see


