A previous article shows a simulation of two different models of a foraging animal. The first model is a random walk, which assumes that the animal chooses a random direction, then takes a step that is distributed according to a Gaussian random variable. In the second model, the animal again
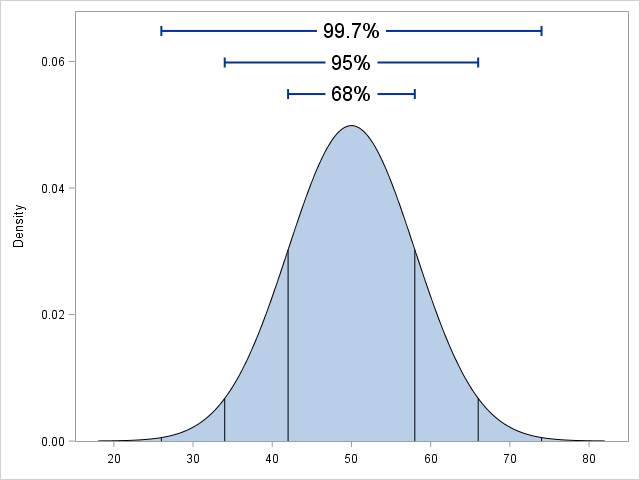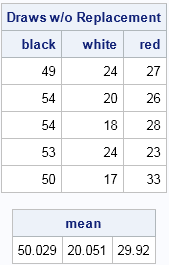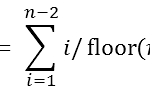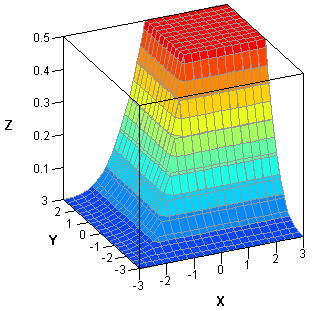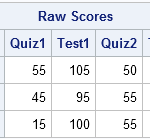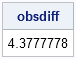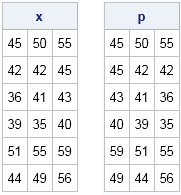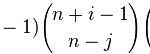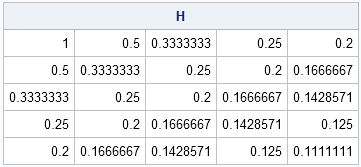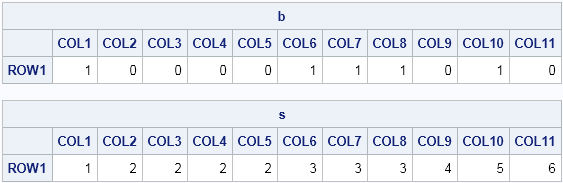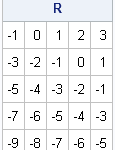
The area of a convex hull enables you to estimate the area of a compact region from a set of discrete observations. For example, a biologist might have multiple sightings of a wolf pack and want to use the convex hull to estimate the area of the wolves' territory. A
In a matrix-vector language such as SAS/IML, it is useful to always remember that the fundamental objects are matrices and that all operations are designed to work on matrices. (And vectors, which are matrices that have only one row or one column.) By using matrix operations, you can often eliminate
