Blogs

Blogs

Find a pattern in a sequence of digits

23
By Topics | Programming Tips

I recently needed to solve a fun programming problem. I challenge other SAS programmers to solve it, too! The problem is easy to state: Given a long sequence of digits, can you write a program to count how many times a particular subsequence occurs? For example, if I give you a sequence of 1,000 digits, can you determine whether the five-digit pattern {1 2 3 4 5} appears somewhere as a subsequence? How many times does it appear?

If the sequence is stored in a data set with one digit in each row, then SAS DATA step programmers might suspect that the LAG function will be useful for solving this problem. The LAG function enables a DATA step to examine the values of several digits simultaneously.

The SAS/IML language also has a LAG function which enables you to form a matrix of lagged values. This leads to an interesting way use vectorized computations to solve this problem. The following SAS/IML program defines a small eight-digit set of numbers in which the pattern {1 2 3} appears twice. The LAG function in SAS/IML accepts a vector of lags and creates a matrix where each column is a lagged version of the input sequence: 

/* Find a certain pattern in sequence of digits */
proc iml;
Digit = {1,1,2,3,3,1,2,3};      /* digits to search */
target = {1 2 3};               /* the pattern to find */
p = ncol(target);               /* length of target sequence */
D = lag(Digit, (p-1):0);        /* columns shift the digits */
print D;

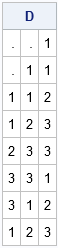
The output shows a three-column matrix (D) that contains the second, first, and zeroth lag (in that order) for the input sequence. Notice that if I am searching for a particular three-digit pattern, this matrix is very useful. The rows of this matrix are all three-digit patterns that appear in the original sequence. Consequently, to search for a three-digit pattern, I can use the rows of the matrix D.

To make the task easier, you can delete the first two rows, which contain missing values. You can also form a binary matrix X that has the value X[i,j]=1 when the j_th element of the pattern equals the j_th element of the i_th row, and 0 otherwise, as shown in the following: 

D = D[p:nrow(Digit),];          /* delete first p rows */
X = (D=target);                 /* binary matrix */
print X;

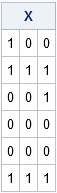
Notice that in SAS/IML, the comparison operator (=) can perform a vector comparison. The binary comparison operator detects that the matrix on the left (D) and the vector on the right (target) both contain three columns. Therefore the operator creates the three-column logical matrix X, as shown. The X matrix has a wonderful property: a row of X contains all 1s if and only if the corresponding row of D matches the target pattern. So to find matches, you just need to sum the values in the rows of X. If the row sum equals the number of digits in the pattern, then that row indicates a place where the target pattern appears in the original sequence.

You can program this test in PROC IML as follows. The subscript reduction operator [,+] is shorthand for "compute the sum of each row over all columns". 

/* sum across columns. Which rows contain all 1s? */
b = (X[,+] = p);                /* b[i]=1 if i_th row matches target */
NumRepl = sum(b);               /* how many times does target appear? */
if NumRepl=0 then 
   print "The target does not appear in the digits";
else
   print "The target appears at location " (loc(b)[1]),  /* print 1st location */
         "The target appears" (NumRepl) "times.";

The program discovered that the target pattern appears in the sequence twice. The first appearance begins with the second digit in the sequence. The pattern also appears in the sequence at the sixth position, although that information is not printed.

Notice that you can solve this problem in SAS/IML without writing any loops. Instead, you can use the LAG function to convert the N-digit sequence into a matrix with N-p rows and p columns. You can then test whether the target pattern matches one of the rows.

Your turn! Can you solve this problem?

Now that I have shown one way to solve the problem, I invite SAS programmers to write their own program to determine whether a specified pattern appears in a numeric sequence. You can use the DATA step, DS2, SQL, or any other SAS language.

Post a comment to submit your best SAS program. Extra points for programs that count all occurrences of the pattern and display the location of the first occurrence.

To help you debug your program, here is test data that we can all use. It contains 10 million random digits: 

data Have(keep=Digit);
call streaminit(31488);
do i = 1 to 1e7;
   Digit = floor(10*rand("uniform"));
   output;
end;
run;

To help you determine if your program is correct, you can use the following results. In this sequence of digits:

  • The five-digit pattern {1 2 3 4 5} occurs 101 times and the first appearance begins at row 34417
  • The six-digit patter {6 5 4 3 2 1} occurs 15 times and the first appearance begins at row 120920

You can verify these facts by using PROC PRINT as follows: 

proc print data=Have(firstobs=34417 obs=34421); run;
proc print data=Have(firstobs=120920 obs=120925); run;

Happy programming!

Tags SAS Programming vectorization
Share

About Author

Rick Wicklin

Distinguished Researcher in Computational Statistics

Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.

23 Comments

  1. Ksharp on

    I am the first one.

    data _null_;
 set have end=last;
 if      digit=5 and 
    lag(digit)=4 and 
    lag2(digit)=3 and
    lag3(digit)=2 and
    lag4(digit)=1 then do;
  n+1;
  if n=1 then do;
      first=_n_-4; 
      put 'first_position=' first;
   end;
 end;
 if last then put 'occur times=' n;
run;
    Reply
  2. Quentin on

    Nifty post, Rick. Here's a brute force approach that builds every string....

    data want;
  set have end=last;
  length string $5 ;
  retain string ;
  string=cat(substrn(string,2,4),digit);
 
  if string="12345" then do;
    position=_n_-4;
    put "Found string at " position=;
    count++1;
  end;
 
  if last then put "Found " count " times";
run;
    Reply
    • Keshan on

      Quentin's code is not efficient due to turn digit into character.
      I would use QUEUE skill.

      data _null_;
 set have end=last;
 array x{5} _temporary_;
 do i=1 to 4;
  x{i}=x{i+1};
 end;
 x{5}=digit;
 if x{1}=1 and 
    x{2}=2 and 
    x{3}=3 and 
    x{4}=4 and 
    x{5}=5 then do;
    n+1;
	if n=1 then do;
         first=_n_-4; 
         put 'first_position=' first;
    end;
 end;
 if last then put 'occur times=' n;
run;
      Reply
  3. Eric on

    Third. Learned this merge "trick" far back in the 90s.

    data want;
   merge have (           rename=(digit=d1))
         have (firstobs=2 rename=(digit=d2))
         have (firstobs=3 rename=(digit=d3))
         have (firstobs=4 rename=(digit=d4))
         have (firstobs=5 rename=(digit=d5))
         have (firstobs=6 rename=(digit=d6));
 
   retain first1 first2 found1 found2 0;
   if d1*10000+d2*1000+d3*100+d4*10+d5 = 12345 then do;
      if not first1 then first1 = _N_;
      found1 = found1 + 1;
   end;
   if d1*100000+d2*10000+d3*1000+d4*100+10*d5+d6 = 654321 then do;
      if not first2 then first2 = _N_;
      found2 = found2 + 1;
   end;
   call symput("first1", first1);
   call symput("found1", found1);
   call symput("first2", first2);
   call symput("found2", found2);
run;
 
%put First occurrence of 12345 in obs &first1., total number is &found1;
%put First occurrence of 654321 in obs &first2., total number is &found2;
    Reply
    • Rick Wicklin
      Rick Wicklin on

      Nice way to build lagged columns. You could also construct "word" columns like
      w5 = d1*10000+d2*1000+d3*100+d4*10+d5;
      w6 = d1*100000+d2*10000+d3*1000+d4*100+10*d5+d6;
      and then DROP d1-d6 if you wanted a smaller data set.

      Reply
  4. muthia kachirayan on

    I tried the following but I am not getting the totals. I do not have data step debugger to dig into it. However I guess that my idea will work faster. I appreciate if you can point to my mistake.

    data _null_;
   retain count pos freq 0;
   do i = 1 to 5;
      set have ;
      pos + 1;
      if digit ^= i then do; count = 0; leave; end;
      count + 1;
   end;  
   if count = 5 then do;
      freq + 1;
      start = pos - 4;
      put start = freq = ;
   end;
run;
 
data _null_;
   retain count pos freq 0;
   do i = 6 to 1 by -1;
      set have ;
      pos + 1;
      if digit ^= i then do; count = 0; leave; end;
      count + 1;
   end;  
   if count = 6 then do;
      freq + 1;
      start = pos - 5;
      put start = freq = ;
   end;
run;
    Reply
  5. muthia kachirayan on

    I missed the successive ones in my earlier algorithm. The following does.

    data _null_;
retain pos count freq 0;
   set have;
   pos + 1;
   if digit = 1 then count = 1;
   else if count = 1 and digit = 2 then count = 2;
   else if count = 2 and digit = 3 then count = 3;
   else if count = 3 and digit = 4 then count = 4;
   else if count = 4 and digit = 5 then count = 5;
   else count = 0;
   if count = 5 then do;
      start = pos - 4; freq + 1;
      put start = freq = ;
      count = 0;
   end;
run;
 
data _null_;
retain pos count freq 0;
   set have;
   pos + 1;
   if digit = 6 then count = 1;
   else if count = 1 and digit = 5 then count = 2;
   else if count = 2 and digit = 4 then count = 3;
   else if count = 3 and digit = 3 then count = 4;
   else if count = 4 and digit = 2 then count = 5;
   else if count = 5 and digit = 1 then count = 6;
   else count = 0;
   if count = 6 then do;
      start = pos - 5; freq + 1;
      put start = freq = ;
      count = 0;
   end;
run;
    Reply
    • tletri on

      Yes, your idea does work fast.
      I like it for it simplicity and because it just do a one scan of the data file, which could be sometimes very very big, these days.
      With a little help from SAS macros, your code could be like this

      %macro gnTest(pattern);
  if digit=%substr(&pattern,1,1) then count=1;
  %do i=2 %to %length(&pattern);
    else if count=%eval(&i-1) and digit=%substr(&pattern,&i,1) then count=&i;
  %end;
  else count= 0;
%mend;
 
%macro doIt(pattern);
data result(keep=pos freq);
retain count 0;
   set have end=last;
   %gnTest(&pattern);
   if count = %length(&pattern) then do;
      pos= _N_-%length(&pattern)+1;
      freq + 1;
      output;
   end;
run;
proc sql noprint;
  select min(pos), max(freq) into:start, :freq from result;
quit;
%put Pattern=&pattern Start=%cmpres(&Start) Freq=%cmpres(&freq);
%mend;
 
%doIt(12345); 
%doIt(654321);
      Reply

  6. Pingback: Find your birthday in the digits of pi - The DO Loop

  7. Dale McLerran on

    I immediately thought of using a data step merge operation as employed by Eric. His solution is efficient for the problem specified. But I generally dislike the idea of displaying just the first occurrence of an event when there is a reasonably finite list of outcomes of interest. What constitutes a reasonably finite set may be open to question. Without looking at results you posted for the sequence {1 2 3 4 5}, I estimated the number of occurrences as {number of sequences} * {probability of sequence pattern). The number of sequences is 10**7 while the probability of a sequence of 5 digits chosen at random would be 10**(-5). So, we would expect 100 occurrences of {1 2 3 4 5}. With probability 99.9%, the number of 5 digit sequences would be at most 130. Still seems like a finite number to me. With virtually complete certainty, there would be no more than 150 instances found. Enumerating all locations (up to 150 locations) has appeal to me.

    Thus, for EXTRA extra credit, I added a temporary array to store locations of each occurrence of the sequence {1 2 3 4 5} (up to 150 occurrences). All locations are then returned.

    data _null_;
  retain target 12345;
  array StringLocs {150} _temporary_;   /* Array holding up to 150 string locations: automatically retained */
 
  merge Have(           rename=(Digit=Digit1) obs=%sysevalf(1E7-4))  /* Obs and Firstobs combinations */
        Have(firstobs=2 rename=(Digit=Digit2) obs=%sysevalf(1E7-3))  /* ensure that Digit1 through    */
        Have(firstobs=3 rename=(Digit=Digit3) obs=%sysevalf(1E7-2))  /* Digit5 are all nonmissing.    */
        Have(firstobs=4 rename=(Digit=Digit4) obs=%sysevalf(1E7-1))
        Have(firstobs=5 rename=(Digit=Digit5)                     )
		end=lastrec;
 
  /* Construct string and test if string matches target */
  string = 10000*Digit1 + 1000*Digit2 + 100*Digit3 + 10*Digit4 + Digit5;  
  test = (string=target);
 
  /* If string matches target, update number found and appropriate array element */
  if test then do;
    nFound + 1;
	if nFound<=150 then StringLocs{nFound}=_n_;
  end;
 
  /* Produce report when all strings have been tested */
  if lastrec then do;
    if nFound<0 then 
      put "The target does not appear in the digits";
	else do;
      nReport = min(150, nFound);
      put "Total occurrences of target string " target @(35 + length(target)) ": " nFound /
          "Location (string initiation) of first " nReport "instances of target string";
	  do i=1 to nReport;
	    put @10 "Instance: " i 3. @30 "Location: " StringLocs{i} 8.;
	  end;
	end;
  end;
run;
    Reply
  8. Leonid Batkhan on

    Thank you, Rick, for posting this challenging brain exercise. Here is my solution. No lags, no merges, no hard-coded logic. Just assign your pattern value to a macro variable called pattern and run. The output dataset have1 will have number of observations equal to the number of pattern occurrences, each observation will have the occurrence position. Here it goes:

    %let pattern =12345; *654321;
data have1 (keep=position);
	length s $%length(&pattern);
	retain s;
	set have;
	position = _n_ - %length(&pattern) + 1;
	s = substr(s,2) !! put(digit,1.);
	if s EQ "&pattern";
run;
    Reply
  9. umesh gautam on

    Let me know what you guys think of this approach.

    data  _r1(keep=digit row nextrow) 
			_r2(keep=digit row2 nextrow) 
			_r3(keep=digit row3 nextrow)
		  _r4(keep=digit row4 nextrow) 
			_r5(keep=digit row5 nextrow); 
 
	set have; 
*//find digits and assign a row number to a variable;
	if digit=1 then row=_n_; 
	if digit=2 then row2=_n_; 
	if digit=3 then row3=_n_; 
	if digit=4 then row4=_n_; 
	if digit=5 then row5=_n_; 	
 
*//split the 'HAVE' datasets by the digits  and calculate nextrow column by adding +1 to the row column**;
	if n(row)=1 then do;
  nextrow=row+1;
	output _r1;
	end;
 
	if n(row2)=1 then do; 
	nextrow=row2+1;
	output _r2; 
	end;
 
	if n(row3)=1 then do; 
	nextrow=row3+1;
	output _r3; 
  end; 
 
	if n(row4)=1 then do; 
  nextrow=row4+1; 
	output _r4; 
	end;
 
	if n(row5)=1 then do; 
	nextrow=row5+1;
	output _r5;
	end;
 
run; 
**use the nextrow column in the dataset to join all the  dataset
nextrow column in the one datasets must match with the another dataset if there's a sequence. ; 
proc sql; 
	create table all(keep= row  row2 row3 row4 row5 ) as 
	select a.row,a.nextrow,b.row2,b.nextrow as r2row,c.row3,c.nextrow as r3row,d.row4,d.nextrow as r4row,e.row5
	from _r1 a inner join _r2 b 
	on a.nextrow=b.row2 inner join _r3 c 
	on b.nextrow=c.row3 inner join _r4 d 
	on c.nextrow=d.row4 inner join _r5 e 
	on d.nextrow=e.row5;
quit;
    Reply
  10. David Pasta on

    I just want to put in a vote in favor of Leonid Batkhan's solution. I probably would have read in the "matching strings" from a dataset as well rather than using macro variables for each pattern I was searching for, but overall I find that a very elegant solution. One of course could just keep the first and last observations of the output dataset if all you want to know is the first and last locations; one could also keep track of the count and output it. I would wager that it's fast, too, and of course requires minimal storage. Nicely done!

    Reply
  11. Peter on

    sorry to be sooo slow in taking the opportunity
    and apparently repeating a part of Dale's solution - but with even more brevity
    and here is the code

    data found ;
   row +1 ;
   merge have( firstobs=1 rename= digit= d1 )
       have( firstobs=2 rename= digit= d2 )
       have( firstobs=3 rename= digit= d3 )
       have( firstobs=4 rename= digit= d4 )
       have( firstobs=5 rename= digit= d5 )
   ;
* without BY on purpose ;
 if cats( of d1-d5) ='12345' ;
 keep row ;
run ;
    Reply
    • Peter on

      surprised by how much my brief solution (code-wise) is slower than Keshan's (on March 10, 2017 11:35 pm)

      7¼ secs for my 6 statement CATS() based solution against the Keshan's array-shuffle loop which took 1½secs on the same machine

      In future I shall be more careful about making those data-type conversions

      Reply
  12. Ed McMullen on

    Hi All, I love all the solutions here, it shows that how flexible SAS is to accommodate many different approaches to a problem. At first, my program was specific to the sequence 12345 then I modified it into the following macro so any sequence of numbers of any length could be found.

    %macro checkseq(seq);                                                                                                                                        
%let seq_n = %length(&seq);
%put &seq is &seq_n digits long;                                                                                                                                        
%do zz=1 %to &seq_n; 
  %let seq&zz = %substr(&seq,&zz,1); 
%end; 
 
data count; 
  set have; 
  retain n flag firstrow 0; 
 
  chgflag=0; 
  if digit=&seq1 and flag=0 then do; flag=1; chgflag=1; firstrow=_n_; end;                                                              
  %do zz=2 %to &seq_n;                                                                                                                  
    else if digit=&&seq&zz and flag=&zz-1 and chgflag=0 then do; flag=&zz; chgflag=1; end;
  %end; 
  if chgflag=0 then flag=0; 
  if flag=&seq_n then do; 
    n+1; 
    call symput('n_seq',  compress(put(n,8.))); 
    if n=1 then call symput('firstrow', compress(put(firstrow,8.))); 
  end; 
run; 
 
%put The sequence &seq appears &n_seq times and the first occurrence starts at row &firstrow..; 
 
%mend; 
 
%checkseq(12345); 
%checkseq(654321);
    Reply
  13. tletri on

    So this is my very first DS2 program, just for fun ;-))) Thanks Rick.
    The algorithm is based on muthia kachirayan's

    %let pattern=12345; /*** < << ==== Your pattern ***/
%let len=%eval(%length(&pattern)-1);
 
proc ds2;
data Test(overwrite=yes label="Have pattern &pattern");
dcl DOUBLE Position having label 'Pattern position' format commax20.;
keep Position;
dcl SMALLINT PatternCheck [0:&len];
dcl SMALLINT chk; retain chk 0;
dcl BIGINT firstPos; retain firstPos;
dcl BIGINT nOcc;
 
method init();
/*** Let's state the rules ***/
dcl BIGINT pattern;
dcl BIGINT n;
dcl INT i;
pattern= &pattern; n=1E&len;
do i=0 to &len;
PatternCheck[i]= int(pattern/n);
pattern= mod(pattern,n); n= n/10;
end;
end;
 
method run();
set have;
if PatternCheck[chk]=digit then chk+1; else chk= (PatternCheck[0]=digit);
if chk=%eval(&len+1) then do;
Position= _N_- &len; output; chk=0;
firstPos= coalesce(firstPos,Position); nOcc+1;
end;
end;
 
method term();
/*** Reporting ***/
put firstPos= nOcc=;
end;
 
enddata;
run;
quit;
    Reply
  14. Serge GRANDIN on

    I'm looking for a code in an excel file that will predict the most probable " digit " to come next ? If my string belong is in cells A1:A100.

    Example data :
    1123133123314212353346233233333243222331232233336113211523133331323142321113151333223126332213522556 next is 3 can a code work finding the 3 after the 100 string digits ?
    Thank you in advance.
    Serge,

    Reply
    • Rick Wicklin
      Rick Wicklin on

      Tabulate the frequencies of the digits. The one that occurs the most is the most probable. In your example, 3 occurs 40 times, which is more than any other digits 1-6. Good luck.

      Reply

Leave A Reply

Back to Top