It is time for Pi Day, 2017! Every year on March 14th (written 3/14 in the US), geeky mathematicians and their friends celebrate "all things pi-related" because 3.14 is the three-decimal approximation to pi. This year I use SAS software to show an amazing fact: you can find your birthday (or any other date) within the first 10 million digits of pi!
Patterns within the digits in pi
Mathematicians conjecture that the decimal expansion of pi exhibits many properties of a random sequence of digits. If so, you should be able to find any sequence of digits within the decimal digits of pi.
If you want to search for a particular date, such as your birthday, you need to choose a pattern of digits that represents the date. For example, Pi Day was first celebrated on 14MAR1988. You can represent that date in several ways. This article uses the MMDDYY representation, which is 031488. You could also use a representation such as 31488, which drops the leading zero for months or days less than 10. Or use the DDMMYY convention, which is 140388.
In 2015 I showed how to use SAS software to download the first ten million digits of pi from an internet site. The program then uses PROC PRINT to print six consecutive digits of pi beginning at the 433,422th digit:
/* read data over the internet from a URL */ filename rawurl url "http://www.cs.princeton.edu/introcs/data/pi-10million.txt" /* proxy='http://yourproxy.company.com:80' */ ; data PiDigits; infile rawurl lrecl=10000000; input Digit 1. @@; Position = _n_; run; /* Pi Day "birthday" 03/14/88 represented as 031488 */ proc print noobs data=PiDigits(firstobs=433422 obs=433427); var Position Digit; run; |
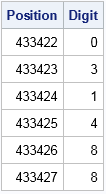
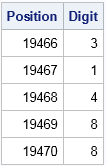
Look at that! The six-digit pattern 031488 appears in the decimal digits of pi! This location also contains the alternative five-digit representation 31488, but you can find that five-digit sequence much earlier, at the 19,466th digit:
/* Alternative representation: Pi Day birthday = 31488 */ proc print noobs data=PiDigits(firstobs=19466 obs=19470); var Position Digit; run; |
How did I know where to look for these patterns? Read on to discover how to use SAS to find a particular pattern digits within the decimal expansion of pi.
Finding patterns within the digits in pi
Last week I showed how to use SAS to search for a particular pattern within a long sequence of digits. Let's use that technique to search for the six-digit Pi Day "birthday," pattern 031488. The following call to PROC IML in SAS defines a function that implements the search algorithm. The program then reads in the first 10 million digits of pi and conducts the search for the pattern:
proc iml; /* FindPattern: Finds a specified pattern within a long sequence of digits. Input: target : row vector of the target pattern, such as {0 3 1 4 8 8} digits : col vector of the digits in which to search Prints the number of times the pattern appears and the first location of the pattern. See https://blogs.sas.com/content/iml/2017/03/10/find-pattern-in-sequence-of-digits.html */ start FindPattern(target, digits); p = ncol(target); /* length of target sequence */ D = lag(digits, (p-1):0); /* columns shift the digits */ D = D[p:nrow(digits),]; /* delete first p rows */ X = (D=target); /* binary matrix */ /* sum across columns. Which rows contain all 1s? */ b = (X[,+] = p); /* b[i]=1 if i_th row matches target */ NumRepl = sum(b); /* how many times does target appear? */ if NumRepl=0 then FirstLoc = 0; else FirstLoc = loc(b)[1]; result = NumRepl // FirstLoc; labl = "Pattern = " + rowcat(char(target,1)); /* convert to string */ print result[L=labl F=COMMA9. rowname={"Num Repl", "First Loc"}]; finish; /* read in 10 million digits of pi */ use PiDigits; read all var {"Digit"}; close; target = {0 3 1 4 8 8}; /* six-digit "birthday" of Pi Day */ call FindPattern(target, Digit); target = {3 1 4 8 8}; /* five-digit "birthday" */ call FindPattern(target, Digit); |
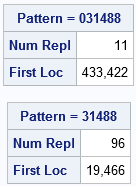
Success! The program shows the starting location for each pattern within the digits of pi. The starting locations match the values of the FIRSTOBS= option that was used in PROC PRINT in the previous section.
Search for your birthday within the digits of pi
You can use this program to search for your birthday, your anniversary, or any other special date. (If you prefer to use the SAS DATA step, see the comments of my previous article.) If you don't have SAS, don't despair! I got the idea for this article from a nifty web page on PBS.org that contains an applet that you can use to find your birthday among the digits of pi.
The PBS applet does not require any special software. However, I noticed that it gives slightly different answers from the SAS program I wrote. One trivial difference is that the applet starts with the "3" digit of pi, whereas the SAS program starts with the "1" in the tenths decimal place. So the two programs should give locations that differ by one place. Another difference is that the applet appears to always represent months and days that are less than 10 as a one-digit value, so that the PBS applet represents 02JAN2003 as "1203" rather than "010203." However, I have observed (but cannot explain) that the PBS applet seems to consistently report a location that is three digits more than the SAS-reported location. For example, the applet reports 02JAN2003 (1203) as occurring at the 60,875th digit, whereas the SAS program reports the location as the 60,872th digit.
Some unique dates within the digits of pi
We know that the Pi Day "birthday" date appears, but what about other dates? I wrote a SAS program that searches for all six-digit MMDDYY representation of dates from 01JAN1900 to 21DEC1999. I verified all dates are contained in the first 10 million digits of pi except for one. The date 01DEC1954 (120154) is the only date that does not appear!
I also discovered some other interesting properties while searching for dates (in the MMDDYY format) within the first 10 million digits of pi:
- First appearance: The first date to appear is 28JUN1962 (062862), which appears in the 71st decimal location.
- Latest (first) appearance: The date 23NOV1960 (112360) does not appear until the 9,982,545th location.
- Rarest: The date 01DEC1954 (120154) is the only date that does not appear. (But the five-digit representation (12154) does appear.)
- Second rarest: There are 15 dates that only appear one time.
- Most frequent: The date 22JUL1982 (072282) appears 25 times.
- Distribution of appearances: Most dates appear between seven and 12 times. The following graph shows the distribution of the number of times that each date appears.
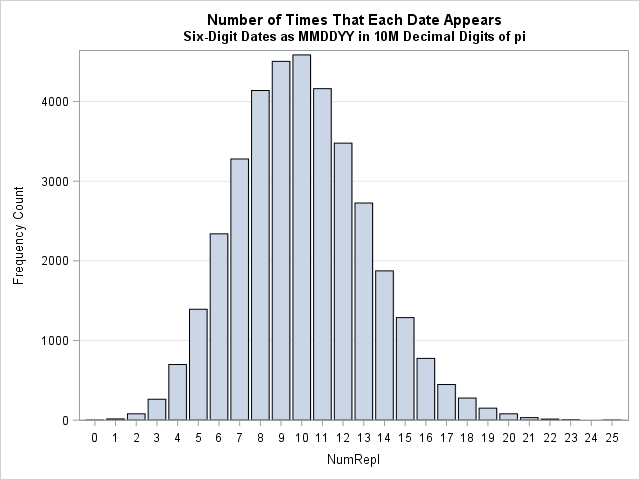
If you want to discover other awesome facts, you can explore the data yourself. You can download the results (in CSV format) of the exhaustive search. If you want to see how I searched the set of all MMDDYY patterns, you can download the SAS program that I used to create the analyses in this article.

9 Comments
My friend Dave D. just told me that his birthday is 01DEC1954, the only date that does not appear in the first 10 million digits of pi. I made him show me his driver's license before I believed him. I feel privileged to know such a unique individual!
Thanks for a great article Rick, and an astonishing coincidence regarding your friend, I am impressed!
I have used your code to look for the famous Six Nines , there are also 7 nines, first location 1,722,776.
Interesting link! I did not know this fact about pi.
Was it the PROC IML step that took three hours? I decided to go the DATA Step route as my PC is pretty old. This code managed to get all the six-digits date strings in about 33 seconds. I found that it didn't matter whether I used the input function with the mmddyy format to find the valid dates or a hash table of all the mmddyy6 dates generated by "01Jan2000"d to "31Dec2099"d (this gets "022900" for the complete and unique set) OR the "old school" building of a format and using the put function. Each method took about 33 seconds. Even more curiously, PROC SUMMARY ran faster with the CLASS statement than the BY statement. I used that to find the first, last and range of occurrence.
Since this used the least amount of code I'll offer this:
filename rawurl url "http://www.cs.princeton.edu/introcs/data/pi-10million.txt";
data PiDigits(index=(six_char_date=(six_char_date) position=(position)/unique));
length six_char_date $6;
infile rawurl lrecl=10000000 truncover;
input Digit $1. @@;
Position=_n_-5;
if position>9999996 then input; *Otherwise data step will never stop;
six_char_date=cat(lag5(digit),lag4(digit),lag3(digit),lag2(digit),lag1(digit),digit);
if input(six_char_date,?? mmddyy6.)^=.;
keep position six_char_date;
run;
The nice thing about this data set with the indexes is that the user can filter it on any date which puts out results very quickly, even on my old PC running SAS University Edition. If there is interest,
As you also found, the mean number of occurences is very close to 10. The variance is also very close to 10 and the skewness is the square root of 0.1 . I think there is something going on here. I think I will try the yymmdd6. format of date representation and see how the statistics compare.
Thanks for the DATA step, Bob. In a previous article, many people submitted ways to use the DATA step (and other techniques) to efficiently search for a pattern in a large data set, but I do not think I have seen the INPUT function with the '??' option used for this purpose. Very interesting technique.
Your comment motivated me to revisit the PROC IML program and make it more efficient. The program now runs in 3 minutes instead of three hours. Thanks for the gentle push.
Rick,
If you use UK dates (DDMMYY), instead of MMDDYY, are there any birthdays that are missing?
...........Phil
What is the proper way 2 write the digits of your birthday
day,month, year- to me makes most sense being that the day comes before the month and the month comes before the year
:-) The millions of people in Europe would agree with you: that is the European standard! Although I live in the US, years of programming in SAS has caused me to write dates as DDMMMYYY, such as 17MAR2018, because that is a common SAS format. I must admit, however, that the mathematician in me prefers YYYYMMDD because then the chronological order matches the alphanumeric (dictionary) order.