Just one last short article about properties of the Hilbert matrix. I've already blogged about how to construct a Hilbert matrix in the SAS/IML language and how to compute a formula for the determinant. One reason that the Hilbert matrix is a famous (some would say infamous!) example in numerical linear algebra is that the inverse matrix is known explicitly and is a matrix of integers. If H is an n x n Hilbert matrix, then the value of the (i,j)th element of the matrix is given by the following formula:
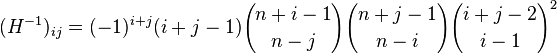
How could you compute the Hilbert inverse in a matrix language such as SAS/IML? The obvious way is to write nested DO loops and call the COMB function in Base SAS to compute the binomial coefficients that appear in the formula, as follows:
proc iml;
n = 5;
/* inverse of Hilbert matrix is a symmetric matrix of large integers */
invH = j(n,n);
do i = 1 to n;
do j = i to n;
b1 = comb(n+i-1, n-j);
b2 = comb(n+j-1, n-i);
b3 = comb(i+j-2, i-1);
invH[i,j] = (-1)##(i+j) # (i+j-1) # b1 # b2 # b3##2;
invH[j,i] = invH[i,j];
end;
end;
print invH; |
For small matrices, nested loops are fine. However, you should assume that someday your program will be used to compute a large matrix. Therefore, you should vectorize the construction so that it avoids using double loops.
The COMB function is a scalar function that computes the number of combinations of r elements taken s at a time. In this definition, r and s are scalar values. But remember that from within the SAS/IML language you can pass matrix arguments to Base SAS functions. If you pass in matrix values for r and s, the COMB function will process the matrices elementwise and return a matrix of binomial coefficients.
Consequently, to vectorize the construction of the Hilbert matrix inverse you need to define i and j so that they are matrices instead of scalars. You can use the ROW function in SAS/IML 12.3 software to construct the i matrix and the COL function to construct the j matrix. (If you do not have SAS/IML 12.3 or later, the functions are defined in a previous blog.)
Therefore you can define the inverse of the Hilbert matrix as follows:
/* compute inverse of nxn Hilbert matrix */ invH = j(n,n); i = row(invH); j = col(invH); /* matrices */ b1 = comb(n+i-1, n-j); /* matrix of binomial coefficients */ b2 = comb(n+j-1, n-i); b3 = comb(i+j-2, i-1); invH = (-1)##(i+j) # (i+j-1) # b1 # b2 # b3##2; |
This examples is applicable to other matrices for which the (i,j)th element is defined by using a formula. The ROW and COL functions enable you to implement the formula and define the matrix without writing any loops over the rows and columns.
