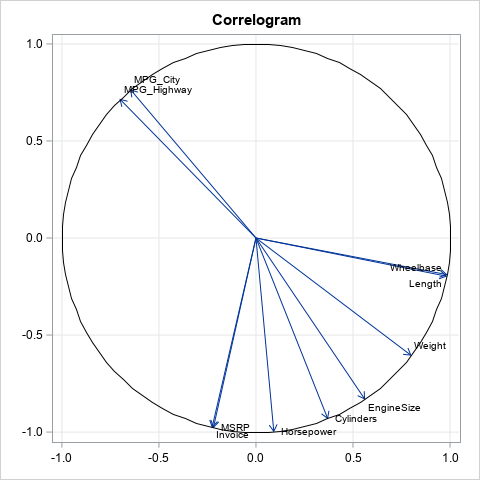
A common way to visualize the sample correlations between many numeric variables is to display a heat map that shows the Pearson correlation for each pair of variables, as shown in the image to the right. The correlation is a number in the range [-1, 1], where -1 indicated perfect