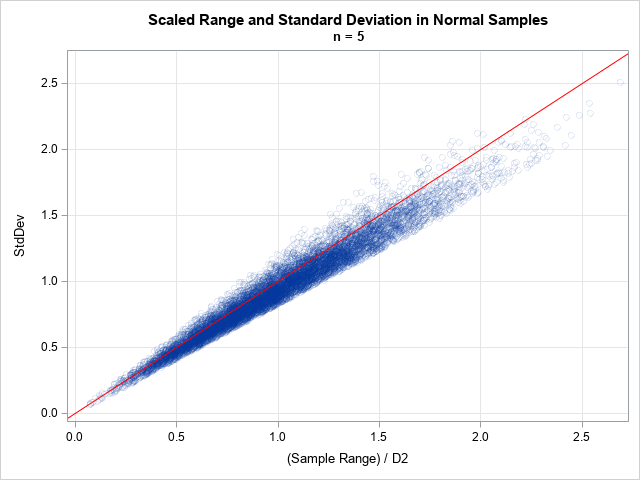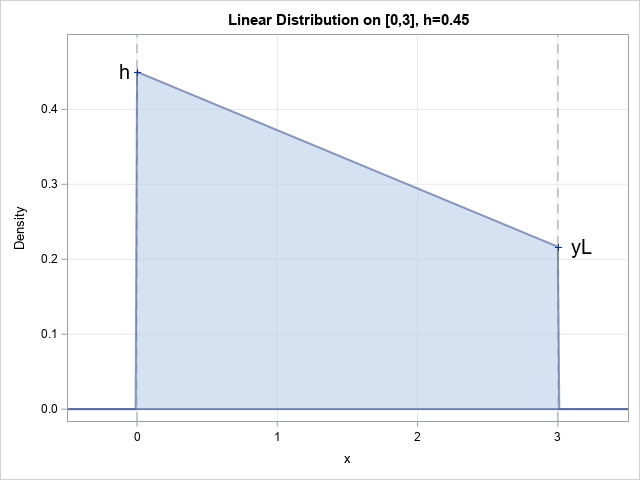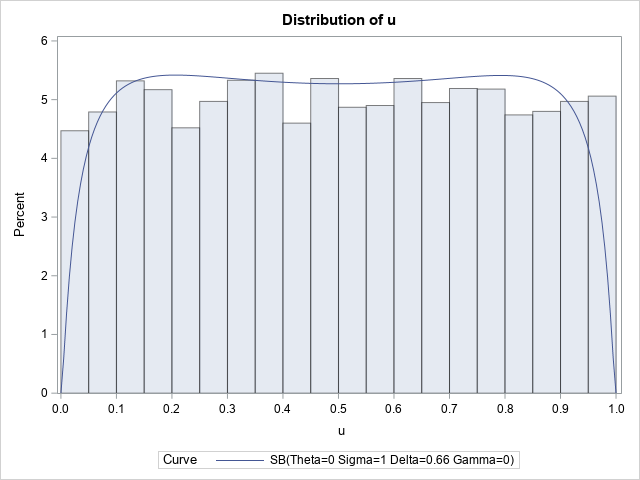
With four parameters I can fit an elephant. With five I can make his trunk wiggle. — John von Neumann Ever since the dawn of statistics, researchers have searched for the Holy Grail of statistical modeling. Namely, a flexible distribution that can model any continuous univariate data. As the quote