The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs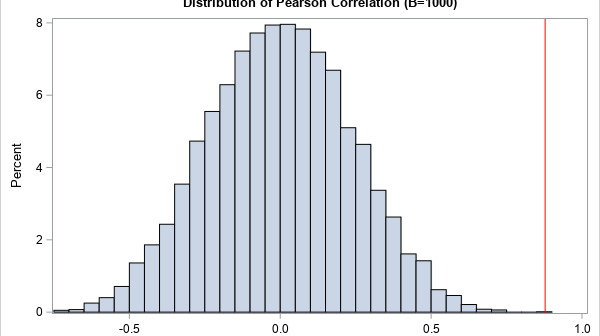
For many univariate statistics (mean, median, standard deviation, etc.), the order of the data is unimportant. If you sort univariate data, the mean and standard deviation do not change. However, you cannot sort an individual variable (independently) if you want to preserve its relationship with other variables. This statement is
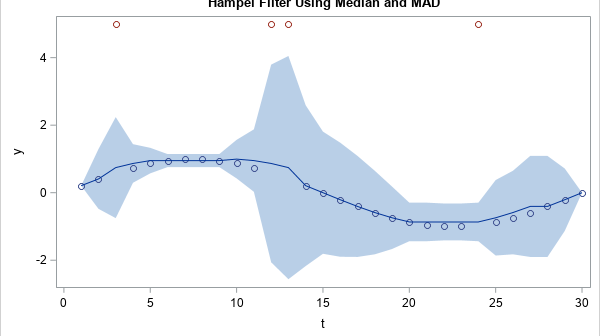
It is well known that classical estimates of location and scale (for example, the mean and standard deviation) are influenced by outliers. In the 1960s, '70s, and '80s, researchers such as Tukey, Huber, Hampel, and Rousseeuw advocated analyzing data by using robust statistical estimates such as the median and the
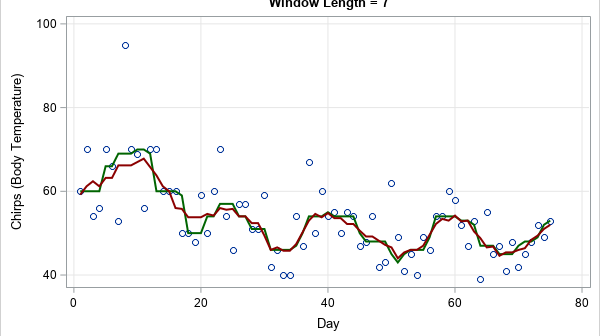
When data contain outliers, medians estimate the center of the data better than means do. In general, robust estimates of location and sale are preferred over classical moment-based estimates when the data contain outliers or are from a heavy-tailed distribution. Thus, instead of using the mean and standard deviation of
I refer to the SAS documentation every day. Usually, I want information about SAS syntax and the statistical formulas and algorithms for various options and statements. Although I have bookmarked common documentation books and chapters, sometimes it is easier to perform an internet search to find information. I've discovered a

A SAS programmer noticed that there is not a built-in function in the SAS DATA step that computes the product for each row across a specified set of variables. There are built-in functions for various statistics such as the SUM, MAX, MIN, MEAN, and MEDIAN functions. But no DATA step

I previously wrote about how to understand standardized regression coefficients in PROC REG in SAS. You can obtain the standardized estimates by using the STB option on the MODEL statement in PROC REG. Several readers have written to ask whether I could write a similar article about the STDCOEF option
