The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
It can be frustrating to receive an error message from statistical software. In the early days of the SAS statistical graphics (SG) procedures, an error message that I dreaded was ERROR: Attempting to overlay incompatible plot or chart types. This error message appears when you attempt to use PROC SGPLOT
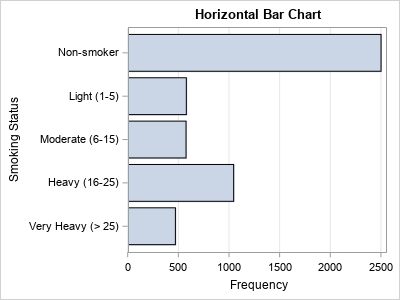
Most introductory statistics courses introduce the bar chart as a way to visualize the frequency (counts) for a categorical variable. A vertical bar chart places the categories along the horizontal (X) axis and shows the counts (or percentages) on the vertical (Y) axis. The vertical bar chart is a precursor
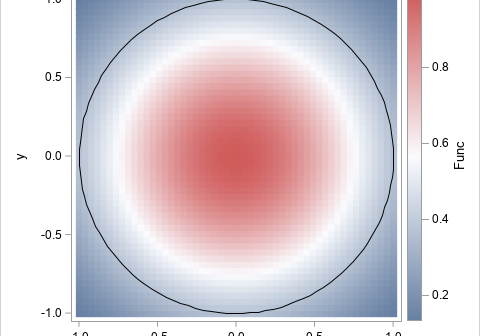
As mentioned in my article about Monte Carlo estimate of (one-dimensional) integrals, one of the advantages of Monte Carlo integration is that you can perform multivariate integrals on complicated regions. This article demonstrates how to use SAS to obtain a Monte Carlo estimate of a double integral over rectangular and
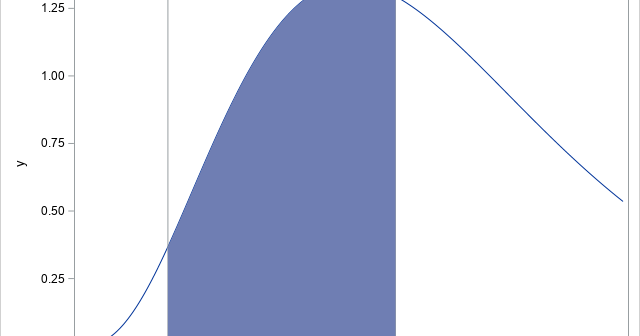
A previous article shows how to use Monte Carlo simulation to estimate a one-dimensional integral on a finite interval. A larger random sample will (on average) result in an estimate that is closer to the true value of the integral than a smaller sample. This article shows how you can

Numerical integration is important in many areas of applied mathematics and statistics. For one-dimensional integrals on the interval (a, b), SAS software provides two important tools for numerical integration: For common univariate probability distributions, you can use the CDF function to integrate the density, thus obtaining the probability that a
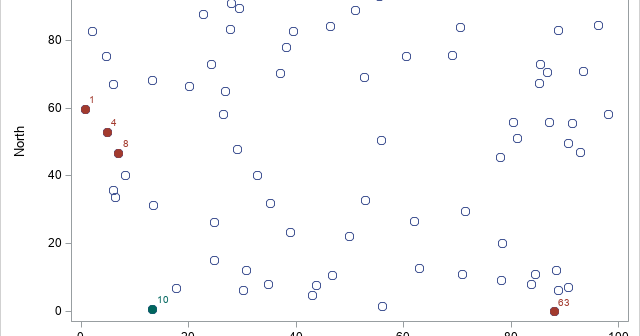
A previous article discusses how to interpret regression diagnostic plots that are produced by SAS regression procedures such as PROC REG. In that article, two of the plots indicate influential observations and outliers. Intuitively, an observation is influential if its presence changes the parameter estimates for the regression by "more
