The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
In computational statistics, there are often several ways to solve the same problem. For example, there are many ways to solve for the least-squares solution of a linear regression model. A SAS programmer recently mentioned that some open-source software uses the QR algorithm to solve least-squares regression problems and asked
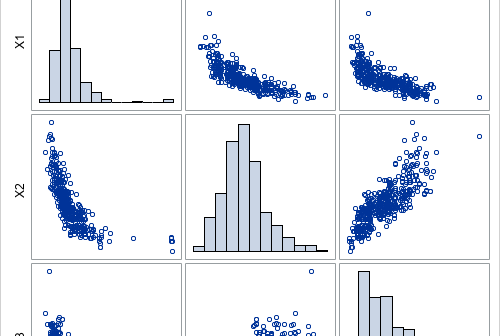
In general, it is hard to simulate multivariate data that has a specified correlation structure. Copulas make that task easier for continuous distributions. A previous article presented the geometry behind a copula and explained copulas in an intuitive way. Although I strongly believe that statistical practitioners should be familiar with
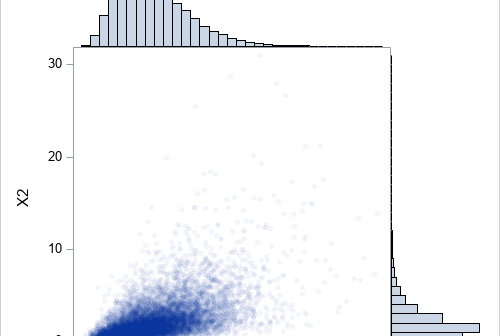
Do you know what a copula is? It is a popular way to simulate multivariate correlated data. The literature for copulas is mathematically formidable, but this article provides an intuitive introduction to copulas by describing the geometry of the transformations that are involved in the simulation process. Although there are

A recent article about how to estimate a two-dimensional distribution function in SAS inspired me to think about a related computation: a 2-D cumulative sum. Suppose you have numbers in a matrix, X. A 2-D cumulative sum is a second matrix, C, such that the C[p,q] gives the sum of

This article shows how to estimate and visualize a two-dimensional cumulative distribution function (CDF) in SAS. SAS has built-in support for this computation. Although the bivariate CDF is not used as much as the univariate CDF, the bivariate version is still a useful tool in understanding the probable values of
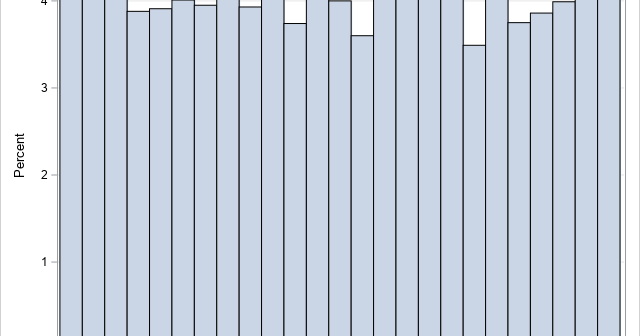
This article uses simulation to demonstrate the fact that any continuous distribution can be transformed into the uniform distribution on (0,1). The function that performs this transformation is a familiar one: it is the cumulative distribution function (CDF). A continuous CDF is defined as an integral, so the transformation is
