The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs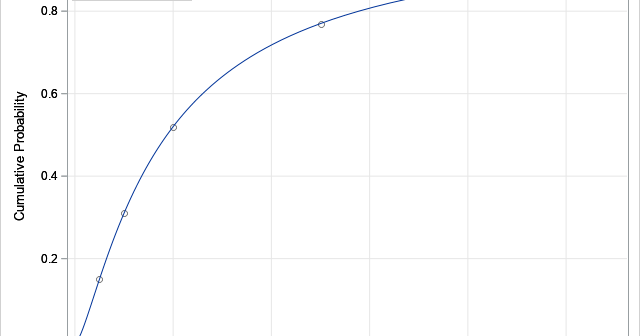
There are many ways to model a set of raw data by using a continuous probability distribution. It can be challenging, however, to choose the distribution that best models the data. Are the data normal? Lognormal? Is there a theoretical reason to prefer one distribution over another? The SAS has
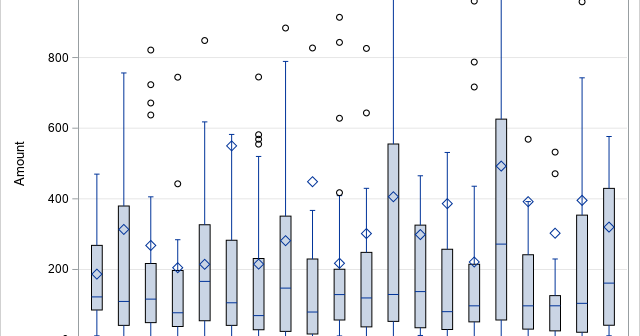
Does anyone write paper checks anymore? According to researchers at the Federal Reserve Bank of Atlanta (Greene, et al., 2020), the use of paper checks has declined 63% among US consumers since the year 2000. The researchers surveyed more than 3,000 consumers in 2017-2018 and discovered that only 7% of
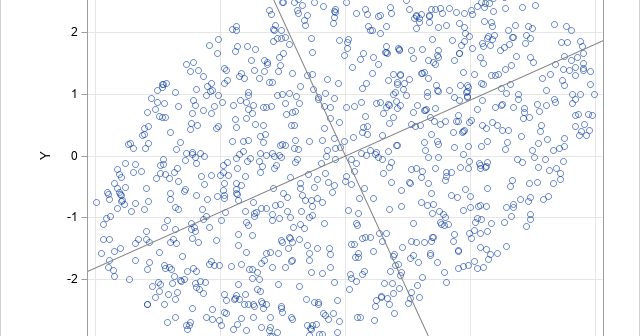
I have previously written about how to efficiently generate points uniformly at random inside a sphere (often called a ball by mathematicians). The method uses a mathematical fact from multivariate statistics: If X is drawn from the uncorrelated multivariate normal distribution in dimensiond, then S = r*X / ||X|| has
