“어떤 알고리즘을 사용해야 할까요?” 수많은 종류의 머신러닝 알고리즘을 맞닥뜨린 초급자 분들이 가장 많이 물어보는 전형적인 질문인데요. 사실 이 질문에 대한 답변은 하단 내용을 비롯한 수많은 요인에 따라 달라집니다.
-
- 데이터의 크기, 품질, 특성
- 가용 연산(계산) 시간
- 작업의 긴급성
- 데이터를 이용해 하고 싶은 것
그렇기에 숙련된 데이터 과학자(Data scientist)조차도 여러 알고리즘을 직접 써보기 전까지는 최고의 성과를 낼 수 있는 최적의 알고리즘을 구별하기란 쉽지 않은데요. 따라서 여러 인공지능(AI)과 머신러닝 전문가들은 해당 분야의 기술을 더욱 빠르게 발전시키기 위해 지식과 경험을 공유하고 있습니다.
지난 7월, 제주도에서 인공지능 기술의 대중화와 연구 활성화를 위한 ‘머신러닝 캠프 제주 2017’이 개최되기도 했는데요. 올해 처음 열린 머신러닝 캠프에는 한국을 비롯해 중국, 미국, 독일, 홍콩, 터키, 헝가리 등 다양한 국적을 가진 개발자들이 참가해 약 한 달간 음성 인식, 기계 번역, 이미지 생성 및 분석 등 머신러닝 분야의 다양한 연구를 진행했습니다.
오늘은 이처럼 여러 데이터 과학자, 머신러닝 전문가, 개발자들의 피드백과 조언을 종합해 초급부터 중급까지의 데이터 과학자와 분석가들을 위한 머신러닝 알고리즘을 추천해드리고자 합니다. 몇몇 확실한 요인에 따라 특정 문제 해결에 적합한 머신러닝 알고리즘을 식별하고, 적용하는 방법을 소개합니다.
<머신러닝 알고리즘 치트 시트>
머신러닝 알고리즘 치트 시트(cheat sheet)는 수많은 머신러닝 알고리즘 중에서 특정 문제에 적합한 알고리즘을 선택할 수 있도록 도와줍니다. 지금부터 치트 시트 사용 방법을 순서대로 살펴보겠습니다.
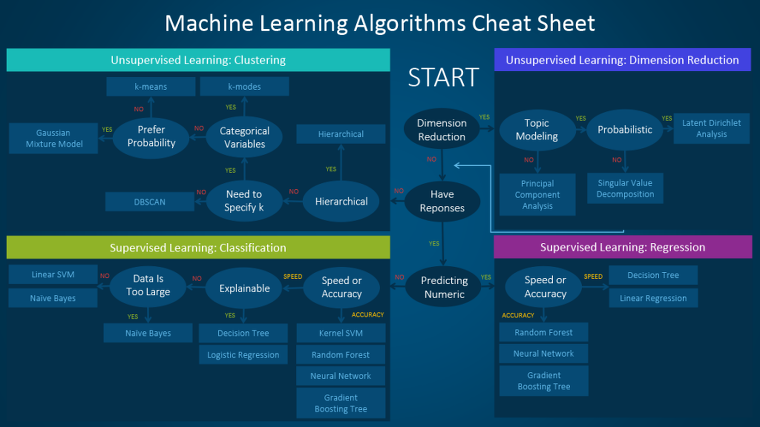
치트 시트는 초급 데이터 과학자와 분석가를 위해 설계됐기 때문에 알고리즘에 대해 논의하기에 앞서 몇몇 단순한 가정을 세우고자 합니다. 오늘 추천하는 모든 알고리즘은 여러 데이터 과학자와 머신러닝 전문가 및 개발자의 피드백과 조언을 종합한 결과입니다. 그 중 상호 합의되지 않은 여러 이슈에 대해서는 공통성을 중심으로 차이를 조정하고자 합니다. 사용 가능한 방법 세트를 계속해서 보강하고 있기 때문에 추후 알고리즘이 추가될 예정입니다.
치트 시트 사용 방법
우선 차트에 나오는 경로(path)와 알고리즘 레이블(label)을 다음과 같이 읽습니다.
If <path label> then use <algorithm>
(만약 <경로 레이블>이면 <알고리즘>을 사용한다)
예를 들어볼까요?
If you want to perform dimension reduction then use principal component analysis.
(차원 축소를 수행하고 싶으면 주성분 분석을 사용한다.)
If you need a numeric prediction quickly, use decision trees or logistic regression.
(신속한 수치 예측이 필요하면 의사결정 트리 또는 로지스틱 회귀를 사용한다.)
If you need a hierarchical result, use hierarchical clustering.
(계층적 결과가 필요하면 계층적 클러스터링을 사용한다.)
한 개 이상의 줄기(branch)가 적용될 때도 있고, 또 때로는 하나도 완벽하게 들어맞지 않을 텐데요. 이 경로들은 통상적인 경험에 비춘 권고 사항이며, 일부는 정확하지 않다는 사실을 꼭 기억해주세요. 몇몇 데이터 과학자들은 “최고의 알고리즘을 찾는 단 하나의 확실한 방법은 모든 알고리즘을 시도해보는 것”이라고 말하기도 합니다.
<머신러닝 알고리즘의 유형>
이번에는 가장 많이 사용되는 머신러닝 유형에 대해 간단하게 살펴보겠습니다. 이미 잘 알고 있다면 특정 알고리즘에 대해 설명하는 다음 단락으로 넘어가셔도 좋습니다.
1. 지도 학습(Supervised learning)
지도 학습 알고리즘은 한 세트의 사례들을(examples) 기반으로 예측을 수행합니다. 예를 들어, 과거 매출 이력(historical sales)을 이용해 미래 가격을 추산할 수 있습니다. 지도 학습에는 기존에 이미 분류된 학습용 데이터(labeled training data)로 구성된 입력 변수와 원하는 출력 변수가 수반되는데요. 알고리즘을 이용해 학습용 데이터를 분석함으로써 입력 변수를 출력 변수와 매핑시키는 함수를 찾을 수 있습니다. 이렇게 추론된 함수는 학습용 데이터로부터 일반화(generalizing)를 통해 알려지지 않은 새로운 사례들을 매핑하고, 눈에 보이지 않는 상황(unseen situations) 속에서 결과를 예측합니다.
-
- 분류(Classification): 데이터가 범주형(categorical) 변수를 예측하기 위해 사용될 때 지도 학습을 ‘분류’라고 부르기도 합니다. 이미지에 강아지나 고양이와 같은 레이블 또는 지표(indicator)를 할당하는 경우가 해당되는데요. 레이블이 두 개인 경우를 ‘이진 분류(binary classification)’라고 부르며, 범주가 두 개 이상인 경우는 다중 클래스 분류(multi-class classification)라고 부릅니다.
- 회귀(Regression): 연속 값을 예측할 때 문제는 회귀 문제가 됩니다.
- 예측(Forecasting): 과거 및 현재 데이터를 기반으로 미래를 예측하는 과정입니다. 예측은 동향(trends)을 분석하기 위해 가장 많이 사용되는데요. 예를 들어 올해와 전년도 매출을 기반으로 내년도 매출을 추산하는 과정입니다.
2. 준지도 학습(Semi-supervised learning)
지도 학습은 데이터 분류(레이블링) 작업에 많은 비용과 시간이 소요될 수 있다는 단점을 지닙니다. 따라서 분류된 자료가 한정적일 때에는 지도 학습을 개선하기 위해 미분류(unlabeled) 사례를 이용할 수 있는데요. 이때 기계(machine)는 온전히 지도 받지 않기 때문에 “기계가 준지도(semi-supervised)를 받는다”라고 표현합니다. 준지도 학습은 학습 정확성을 개선하기 위해 미분류 사례와 함께 소량의 분류(labeled) 데이터를 이용합니다.
3. 비지도(자율) 학습(Unsupervised learning)
비지도 학습을 수행할 때 기계는 미분류 데이터만을 제공 받습니다. 그리고 기계는 클러스터링 구조(clustering structure), 저차원 다양체(low-dimensional manifold), 희소 트리 및 그래프(a sparse tree and graph) 등과 같은 데이터의 기저를 이루는 고유 패턴을 발견하도록 설정됩니다.
-
- 클러스터링(Clustering): 특정 기준에 따라 유사한 데이터 사례들을 하나의 세트로 그룹화합니다. 이 과정은 종종 전체 데이터 세트를 여러 그룹으로 분류하기 위해 사용되는데요. 사용자는 고유한 패턴을 찾기 위해 개별 그룹 차원에서 분석을 수행할 수 있습니다.
- 차원 축소(Dimension Reduction): 고려 중인 변수의 개수를 줄이는 작업입니다. 많은 애플리케이션에서 원시 데이터(raw data)는 아주 높은 차원의 특징을 지니는데요. 이때 일부 특징들은 중복되거나 작업과 아무 관련이 없습니다. 따라서 차원수(dimensionality)를 줄이면 잠재된 진정한 관계를 도출하기 용이해집니다.
4. 강화 학습(Reinforcement learning)
강화 학습은 환경으로부터의 피드백을 기반으로 행위자(agent)의 행동을 분석하고 최적화합니다. 기계는 어떤 액션을 취해야 할지 듣기 보다는 최고의 보상을 산출하는 액션을 발견하기 위해 서로 다른 시나리오를 시도합니다. 시행 착오(Trial-and-error)와 지연 보상(delayed reward)은 다른 기법과 구별되는 강화 학습만의 특징입니다.
<알고리즘 선택 시 고려 사항>
알고리즘을 선택할 때에는 언제나 정확성, 학습 시간, 사용 편의성을 고려해야 합니다. 많은 경우 정확성을 최우선으로 두는데요. 반면 초급자는 가장 잘 알고 있는 알고리즘에 초점을 맞추는 경향이 있습니다.
데이터 세트가 제공됐을 때 가장 먼저 고려해야 할 것은 ‘어떤 결과가 나올 것인지에 상관없이 어떻게 결과를 얻을 것인가’입니다. 초급자일수록 실행하기 쉽고 결과를 빨리 얻을 수 있는 알고리즘을 선택하기 쉬운데요. 프로세스의 첫 단계에서는 괜찮을 수 있겠지만 일부 결과를 얻었고 데이터에 익숙해진 후라면 정교한 알고리즘을 사용하는 데 시간을 더 많이 할애해야 합니다. 그래야만 데이터를 더욱 잘 이해하고, 결과를 개선시킬 수 있습니다.
심지어 이 단계에서조차도 최상의 알고리즘은 가장 높은 정확성을 달성한 방법이 아닐 수 있습니다. 일반적으로 알고리즘은 달성 가능한 최고의 성능을 발휘하기 위해 세심한 튜닝(tuning)과 광범위한 학습을 요구하기 때문입니다.
<특정 알고리즘을 사용하는 시점>
개별 알고리즘을 보다 자세히 들여다보면 알고리즘이 무엇을 제공하고, 어떻게 사용되는지 이해하는 데 도움이 되는데요. 이번에는 치트 시트를 기반으로 보다 자세한 정보와 함께 특정 알고리즘을 사용하는 시점에 대해 추가 팁을 드리고자 합니다.
1. 선형 회귀(Linear regression)와 로지스틱 회귀(Logistic regression)
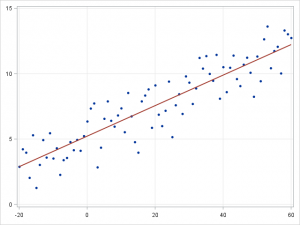
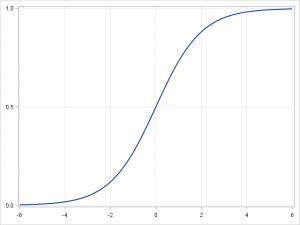
▲선형 회귀(왼쪽)와 로지스틱 회귀(오른쪽)
선형 회귀는 연속적인 종속 변수 
종속 변수가 연속형이 아니라 범주형이라면 선형 회귀는 로짓 연결(logit link) 함수를 이용해 로지스틱 회귀로 변환될 수 있습니다. 로지스틱 회귀는 단순하고 빠르지만 강력한 분류 알고리즘인데요. 여기에서는 종속 변수 
로지스틱 회귀에서는 주어진 자료가 
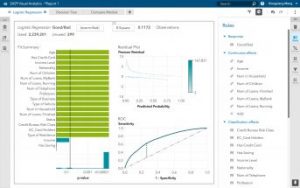
▲그룹별 선형 회귀(왼쪽)와 ‘SAS 비주얼 애널리틱스’의 로지스틱 회귀(오른쪽)
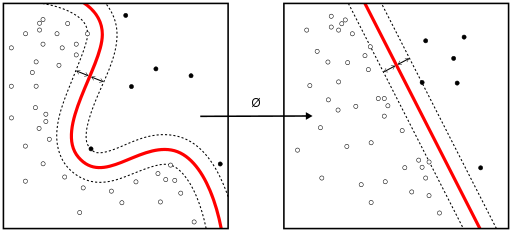
2. 선형(Linear) SVM 및 커널(Kernel) SVM
커널 트릭(기법)은 분리 가능한 비선형 함수를 고차원의 분리 가능한 선형 함수로 매핑하기 위해 사용됩니다. 서포트 벡터 머신(SVM; support vector machine) 학습 알고리즘은 초평면(hyperplane)의 법선 벡터(normal vector) ‘w’와 편향 값(bias) ‘b’로 표현되는 분류기(classifier)를 찾습니다. 이러한 초평면(경계)은 가능한 최대 오차(margin)로 각기 다른 클래스를 분리하는데요. 그러면 문제를 제약 조건이 있는(constrained) 최적화 문제로 변환할 수 있습니다.
3. 트리와 앙상블 트리(ensemble tree)
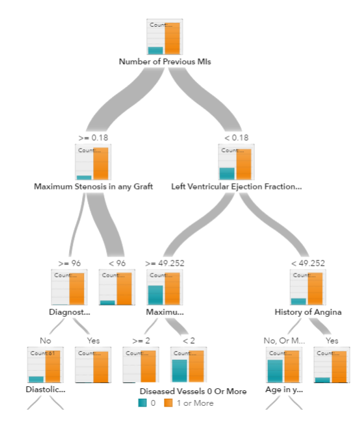
의사결정 트리, 랜덤 포레스트(random forest), 그래디언트 부스팅(gradient boosting)은 모두 의사결정 트리를 기반으로 한 알고리즘입니다. 다양한 종류의 의사결정 트리가 있지만, 모두 동일한 작업을 수행합니다. 즉 특징 공간(feature space)을 거의 같은 레이블로 구별되도록 분리합니다. 의사결정 트리는 이해와 구현이 쉽지만 가지를 다 쳐내고 트리의 깊이가 너무 깊어질 경우 데이터를 과적합(overfit)하는 경향이 있습니다. 랜덤 포레스트와 그래디언트 부스팅은 일반적으로 높은 정확성을 달성하고 과적합 문제를 해결하기 위해 트리 알고리즘을 사용하는 두 가지 방법입니다.
4. 신경망과 딥러닝
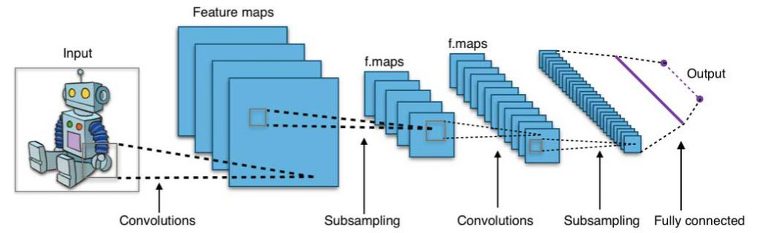
신경망은 병렬 분산 처리 능력 덕분에 1980년대 중반 크게 성장했습니다. 그러나 신경망 매개 변수를 최적화하기 위해 널리 사용되는 역전파(back-propagation) 학습 알고리즘이 효과가 없어 신경망 연구가 지연됐는데요. 이후 컨벡스(볼록) 최적화(convex optimization) 문제가 해결됨으로써 쉽게 학습할 수 있는 서포트 벡터 머신(SVM)과 여타 단순한 다른 모델들이 서서히 머신러닝의 신경망을 대체했습니다.
최근 몇 년간 새롭게 개선된 비지도 사전 학습(unsupervised pre-training)과 계층별 탐욕 학습(layer-wise greedy training) 등의 학습 기법들은 신경망에 대한 관심을 부활시키는 계기가 됐는데요. 또 GPU(graphical processing unit)와 MPP(massively parallel processing)와 같이 점차 강력해지는 연산 능력은 신경망을 다시 채택하게 하는 원동력이 됐습니다. 신경망 연구가 재개되면서, 수천 개의 계층을 가진 모델이 개발되기 시작했습니다.
다시 말해, 얕은(shallow) 신경망이 딥러닝 신경망으로 진화한 것이죠! 심층(deep) 신경망은 지도 학습에 매우 성공적이었습니다. 딥러닝은 음성이나 이미지 인식에 사용될 때 인간만큼 또는 심지어 인간보다 더 나은 성능을 보입니다. 또 딥러닝은 특징 추출(feature extraction)과 같은 비지도 학습 과제에 적용될 때 인간의 개입이 훨씬 줄어든 상황에서 원시 이미지(raw images)나 음성으로부터 특징을 추출할 수 있죠.
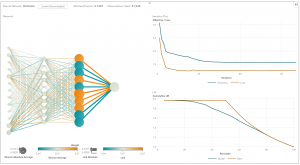
신경망은 입력 계층(input layer), 은닉 계층(hidden layers), 출력 계층(output layer)의 세 부분으로 구성됩니다. 학습 표본(training samples)은 입력 및 출력 계층을 정의하는데요. 출력 계층이 범주형 변수일 때 신경망은 분류 문제를 해결합니다. 출력 계층이 연속 변수일 때 신경망은 회귀 작업을 위해 사용될 수 있습니다. 또 출력 계층이 입력 계층과 동일할 때 신경망은 고유한 특징을 추출하기 위해 사용될 수 있습니다. 이때 은닉 계층의 수는 모델 복잡성과 모델링 수용력(capacity)을 결정합니다.
5. K-평균/K-모드(k-means/k-modes), 가우시안 혼합 모델(GMM; Gaussian mixture model) 클러스터링
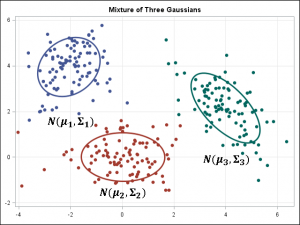
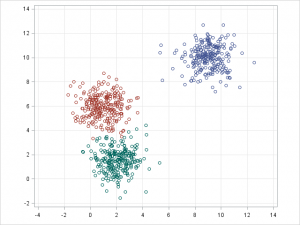
K-평균/K-모드 클러스터링과 GMM 클러스터링의 목표는 n개의 관측치(observations)를 k개의 클러스터로 나누는 것입니다. K-평균은 표본을 하나의 클러스터에만 강하게 결속시키는 ‘하드 할당(hard assignment)’를 정의합니다. 반면 GMM은 각 표본이 확률 값을 가짐으로써 어느 한 클러스터에만 결속되지 않는 ‘소프트 할당(soft assignment)’을 정의하는데요. 두 알고리즘 모두 클러스터 k의 수가 주어질 때 클러스터링을 빠르고 단순하게 수행할 수 있습니다.
6. DBSCAN
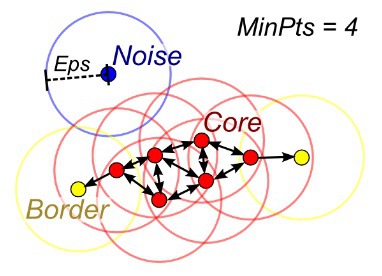
클러스터 k의 수가 주어지지 않을 때에는 밀도 확산(density diffusion)을 통해 표본을 연결함으로써 DBSCAN(density-based spatial clustering)을 사용할 수 있습니다.
7. 계층적 군집화(Hierarchical clustering)
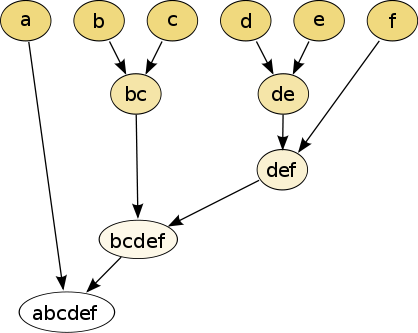
계층적 분할은 트리 구조인 덴드로그램(dendrogram)를 이용해 시각화할 수 있습니다. 각기 다른 K를 사용해 클러스터를 정제하거나 조대화할 수 있는 각기 다른 세분화(granularities) 수준에서 입력과 분할 결과를 확인할 수 있기 때문에 클러스터의 개수가 필요 없습니다.
8. PCA, SVD, LDA
일반적으로 머신러닝 알고리즘에 많은 수의 특징을 직접 투입하는 것은 선호되지 않습니다. 일부 특징은 관련이 없거나 ‘고유한’ 차원수가 특징의 수보다 적을 수 있기 때문인데요. 따라서 주성분 분석(PCA; principal component analysis), 특이값 분해(SVD; singular value decomposition), 잠재 디리클레 할당(LDA; latent Dirichlet allocation)을 이용해 차원 축소를 수행할 수 있습니다.
PCA는 원래의 데이터 공간을 저차원의 공간으로 매핑하면서 가능한 많은 정보를 보존하는 비지도 클러스터링 방식입니다. PCA는 기본적으로 데이터 분산(variance)을 가장 많이 보존하는 하위 공간(subspace)을 찾는데요. 하위 공간은 데이터의 공분산 매트릭스(covariance matrix)의 지배적인 고유 벡터(eigenvectors)에 따라 정의됩니다.
SVD는 중앙 데이터 매트릭스의 SVD(특징 vs. 표본)가 PCA로 찾은 것과 동일한 하위 공간을 정의하는 지배적인 왼쪽 특이 벡터(left singular vectors)를 제공한다는 점에서 PCA와 관련되어 있습니다. 그러나 SVD는 PCA가 할 수 없는 작업을 수행할 수 있기 때문에 훨씬 다재다능한 기법인데요. 예를 들어, 사용자 대 영화 매트릭스의 SVD는 추천 시스템에서 사용할 수 있는 사용자 프로파일과 영화 프로파일을 추출할 수 있습니다. 또 SVD는 자연어 처리(NLP; natural language processing) 과정에서 잠재 의미 분석(latent semantic analysis)으로 알려진 주제 모델링(topic modeling) 도구로서 널리 사용됩니다.
자연어 처리(NLP)와 관련된 기법은 잠재 디리클레 할당(LDA)입니다. LDA는 확률적 주제 모델(probabilistic topic model)로 가우시안 혼합 모델(GMM)이 연속 데이터를 가우시안 밀도로 분해하는 것과 비슷한 방식으로 문서를 주제를 기준으로 분리합니다. GMM과 다르게 LDA는 이산 데이터(discrete data, 문서 내 단어)를 모델링하고, 주제는 디리클레 분포(Dirichlet distribution)에 따라 연역적(priori)으로 분포돼야 하는 제약이 있습니다.
<결론>
지금까지 설명한 워크 플로우는 따라하기 쉽지만, 새로운 문제를 해결해야 한다면 다음의 중요한 메시지를 꼭 기억하세요.
-
- 문제를 정의한다. 어떤 문제를 해결하고 싶은가?
- 단순하게 시작한다. 데이터와 기준이 되는 결과(baseline results)를 잘 인지하고 있어야 한다.
- 그리고 나서 복잡한 것들을 시도한다.
SAS 비주얼 데이터 마이닝(SAS Visual Data Mining)과 머신러닝은 초급자들도 머신러닝을 배우고, 개별 문제에 머신러닝 방법을 적용할 수 있는 뛰어난 플랫폼을 제공합니다. 지금 바로 무료 체험판을 신청해보세요!
