Graphically Speaking
Data Visualization with a focus on SAS ODS Graphics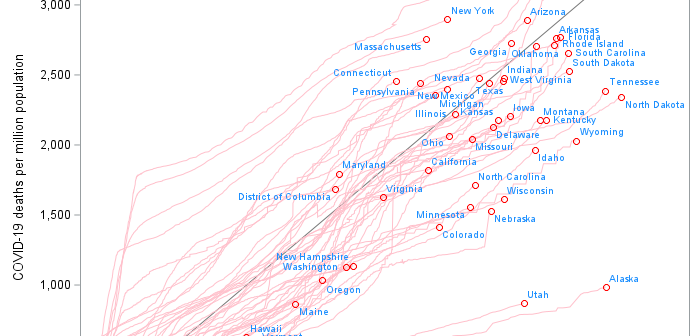
A scatter plot is my go-to graph! It's what I often start with to get a feel for the data ... and I often end up using just a scatter plot. But some scatter plots are better than others ... In this blog post, I create a scatter plot of
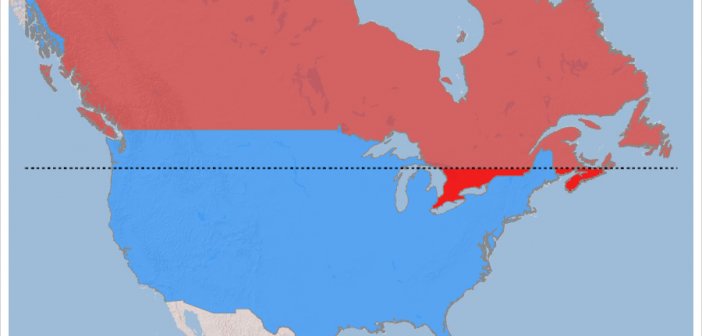
Canada is a geographically large country, but I've heard that much of the population lives in the small southernmost sections (near the US border). I decided to use my mapping skills, and put that to the test. Follow along, and we'll see what that looks like on a map ...
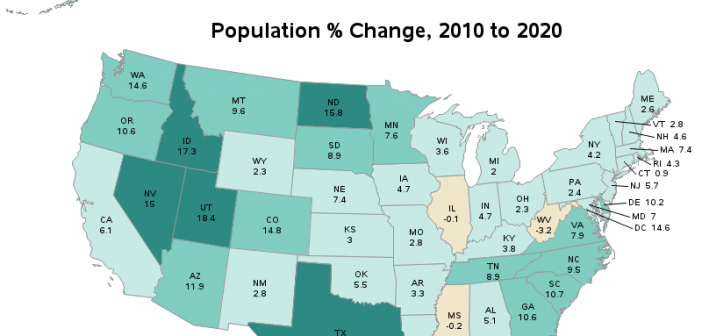
With the 2020 Census numbers starting to come out, it's interesting to look at what states are gaining (or losing) people. In this example, I create a custom map similar to the ones the US Census Bureau likes to use, and plot the 10-year change in population. But before we
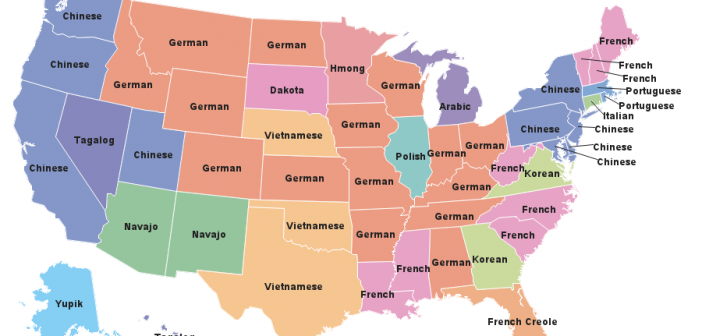
This blog post is mostly just a bunch of fun maps ... maps that are labeled (or mislabeled) in various ways, using fun/interesting data. I focus on the 'fun' part, but if you're not careful you might also learn a little about the various ways to add labels to maps
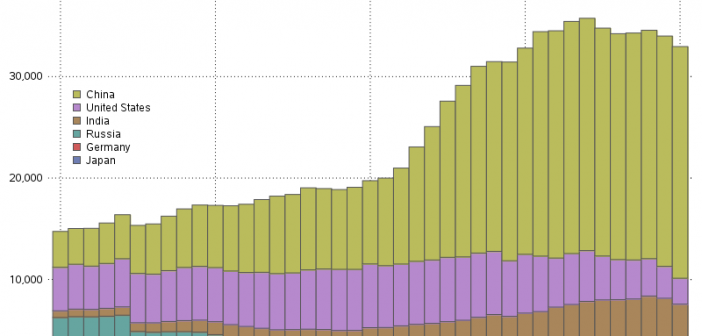
These days, many countries are moving away from coal, and towards natural gas, hydro, wind, and solar as ways to meet their electricity needs. I had heard that some countries still use a lot of coal (especially those countries with large coal deposits), and I was curious which countries use
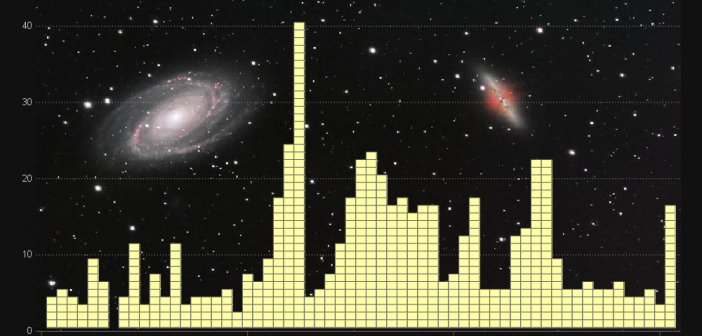
Recently, the news has been all abuzz about William Shatner traveling into space. This was a cool event because he's the oldest person who has traveled into space (at 90 years old) ... and he was also the iconic Captain Kirk from the original Star Trek television series. This got
