The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs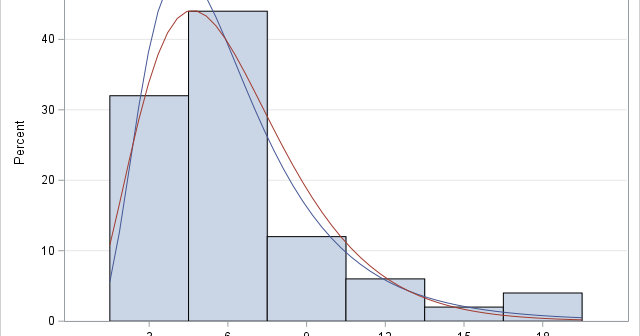
A previous article discusses various ways to overlay a density curve on a histogram in SAS. SAS provides several procedures that handle this task for common univariate probability distributions such as normal, lognormal, and gamma. If you define and use a less common distribution, you can write a GTL template
SAS has several procedures that can fit a probability distribution to data, plot a histogram, and overlay one or more density estimates: PROC UNIVARIATE in Base SAS enables you to overlay parametric density curves from about 20 common continuous probability distributions, such as normal, lognormal, and gamma. It also enables
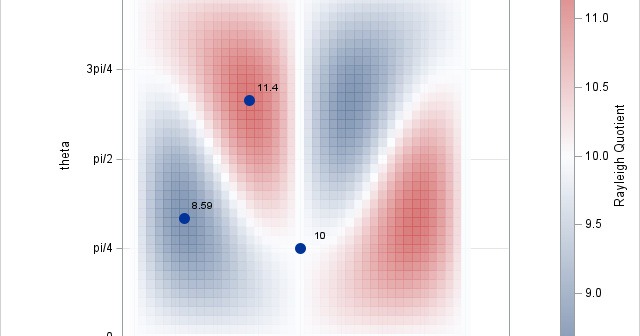
The power method is a well-known iterative scheme to approximate the largest eigenvalue (in absolute value) of a symmetric matrix. It is useful in practice when you need only the largest eigenvalue and eigenvector of a large matrix. The method requires only matrix-vector multiplication and vector scaling. There is a
