Before joining SAS, I was unaware of the possibilities around hyperparameter autotuning. When trying to maximize model performance, I would code up cumbersome pipelines trying multiple hyperparameter values across multiple models. This effort created a better performing model, but it still took up a large chunk of my time. In SAS Visual Data Mining and Machine Learning, adding hyperparameter autotuning only requires an extra line of code or a button click. While SAS searches the hyperparameter space in the background, I am free to pursue other work. Hyperparameter autotuning is now one of my favorite machine learning capabilities (right next to feature machines). Through hyperparameter autotuning, I am maximizing my model's performance without maximizing my effort. Therefore today, I will review what hyperparameters are, how to find which combination of hyperparameters to use, and how to get started using hyperparameter autotuning on SAS Viya.
What are hyperparameters?
Training and tuning a model are two different tasks. In model training, you strive to find the best set of model parameters that map how your inputs affect your target. For instance, coefficient values are the parameters in a regression and splitting rules are parameters in a decision tree. In model tuning, you strive to create the best model configuration for the task at hand. For example, maximum tree depth is a hyperparameter in a decision tree model and the number of hidden layers is a hyperparameter in a neural network.
How can I find which combination of hyperparameters to use?
There are various methods used to search the hyperparameter space for improved model performance. These methods include a grid search, a random search, Latin Hypercube Sampling (LHS), a Genetic Algorithm (GA), and a Bayesian search.
Grid search
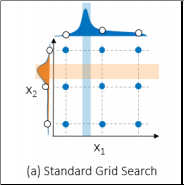
Grid search was my pre-SAS approach to hyperparameter autotuning. The first step of grid search is to take each hyperparameter of interest and select a set of values. Next, models are trained and assessed using the combination of potential hyperparameter values. The best performing models win. The downside of grid search is that it can be computationally costly to create a grid that is granular enough to find the optimal combination. In the figure below, notice that there were nine combinations examined. Even though nine models were trained and assessed, only three potential values were examined for each hyperparameter and the optimal points were missed.
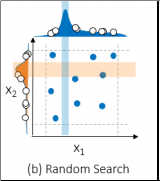
Random search
Random search involves training and assessing models with hyperparameter combinations chosen at random. Consequently, random search may find the optimal combination of hyperparameter by chance! However, random search may miss the optimal points altogether. The figure below also uses nine combinations but it may try more values per hyperparameter.
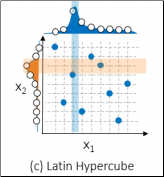
Latin Hypercube Sampling
If a grid search and a random search don't sound optimal - it's because they're not. Therefore to search the hyperparameter space more efficiently, SAS uses Local Search Optimization (LSO) capabilities. Latin Hypercube Sampling (LHS) is one Local Search Optimization strategy. Latin Hypercube Sampling examines more values for each hyperparameter and ensures that each value shows up only once in randomly blended combinations. By identifying good values for each hyperparameter, then stronger combinations can be made from these good values. This strategy allows for a more efficient search using the same number of points. The figure below also uses nine combinations, but examines nine values for each hyperparameter, evenly spread across the entire range to ensure that the full range was studied.
Genetic Algorithm
A Genetic Algorithm (GA) uses the principles of natural selection and evolution to find an optimal set of hyperparameters. First, the Genetic Algorithm will create an initial population using Latin Hypercube Sampling. By default, the number of Latin Hypercube Sampling evaluations used to initialize the Genetic Algorithm is fewer than the number of evaluations used when Latin Hypercube Sampling is used as a search method. Next these configurations can experience cross-over or random mutations to create new configurations. In cross-over events, various hyperparameter combinations are created from the hyperparameter values of the parents. Random mutation events can add new values to hyperparameters at random. An additional Generating Set Search (GSS) step performs local perturbations of the best hyperparameter combinations to add more potential high-performing configurations. Following, the new configurations are evaluated and the best configurations can serve as parents for a new generation of configurations in this iterative process.
Bayesian search
Bayesian search uses a surrogate model to improve upon Latin Hypercube Sampling. Latin Hypercube Sampling is used to initialize a Kriging surrogate model (also known as a Gaussian process surrogate regression) to approximate the objective function. These are probabilistic statistical models that measure the similarity between points to predict unseen points within a finite collection of variables that have a multivariate normal distribution. The surrogate models generate new configurations to evaluate, which are then used to iteratively update the model.
Choosing a search method
Between grid search, random search and Latin Hypercube Sampling, Latin Hypercube Sampling tends to perform better. It is important to note that for grid search, random search, and Latin Hypercube Sampling, all configuration evaluations can be done in parallel, but no learning occurs. With the Genetic Algorithm and Bayesian search, the configuration evaluations within each iteration can be done in parallel, but better configurations can be achieved through learning across sequential iterations.
Ultimately which algorithm runs fastest depends on the resources used to run the algorithm. A system that can run all of the evaluations in parallel would find that grid search, random search, and Latin Hypercube Sampling would run the fastest. Given that such a system may not always be available, there may be smaller or even negligible speed differences across the search methods. Following, better performance on the objective function is more likely to be achieved using a learning-based search like the Genetic Algorithm or Bayesian search. With these considerations, I now see why Genetic Algorithm is the default hyperparameter search method!
How do I get started?
Getting started with hyperparameter autotuning on Viya is a piece of cake! You can build stronger models in Viya's visual interface or programming interface in one or two steps.
SAS Model Studio on Viya
In SAS Model Studio on Viya, autotuning hyperparameters can be added with a single button click. For Bayesian networks, Support Vector Machines (SVM), decision trees, forests, gradient boosting models, and neural networks, hyperparameter autotuning is available in the options.
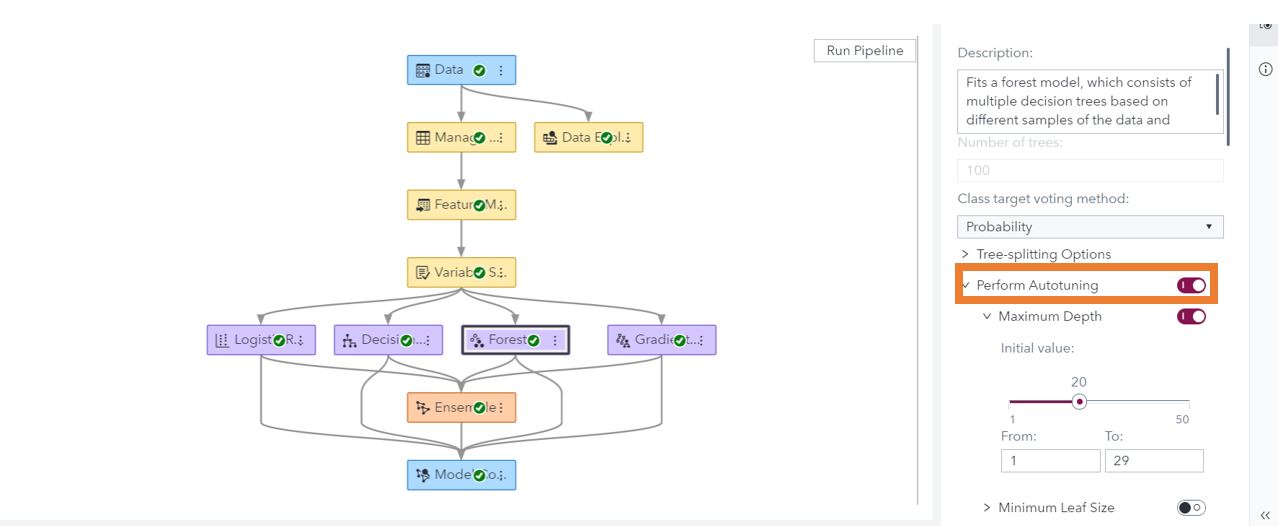
SAS Studio on Viya
To add hyperparameter autotuning to a model created through a task, you only have to click a checkbox. Under the options for the forest, gradient boosting, decision tree, neural network, Support Vector Machine (SVM), and factorization machine tasks include the option for hyperparameter autotuning.
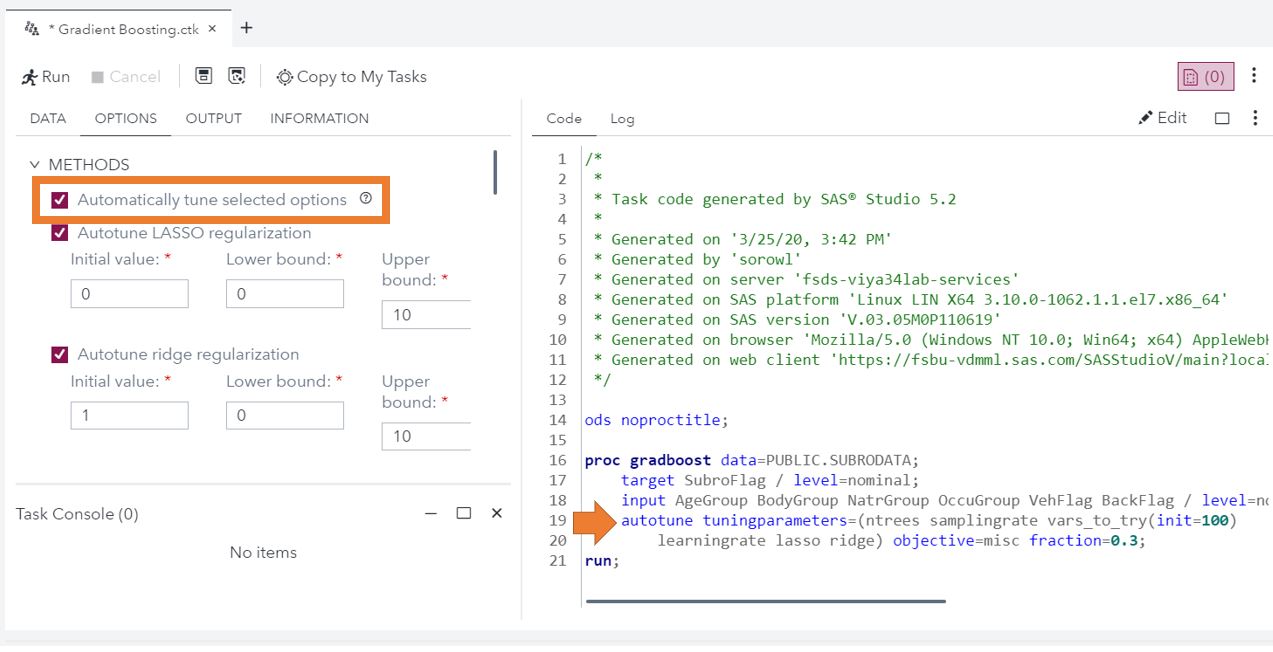
If coding is more your style, for many models Visual Data Mining and Machine Learning (VDMML) procedures (including the gradient boosting example above), hyperparameter autotuning can be added using the autotune statement. Additionally for CASL programming, you can use the Autotune Action Set.
Conclusion
In conclusion, you should be ready to maximize your model's performance without maximizing your effort! If you are interested reading more, this blog goes into depth on autotuning value, this blog discusses autotuning within machine learning best practices, this blog discusses Local Search Optimization for autotuning, this communities article includes a brief overview into autotuning, and this whitepaper and this whitepaper goes into a deep dive into hyperparameter autotuning.
A special thanks to Patrick Koch for his help in refining the search methods pieces of this blog!






