The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs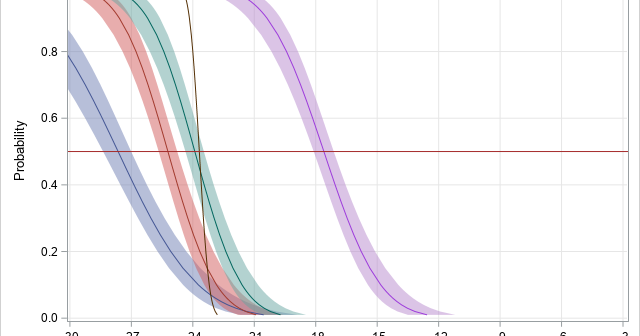
"O Christmas tree, O Christmas tree, how lovely are your branches!" The idealized image of a Christmas tree is a perfectly straight conical tree with lush branches and no bare spots. Although this ideal exists only on Christmas cards, forest researchers are always trying to develop trees that approach the

A SAS customer asked a great question: "I have parameter estimates for a logistic regression model that I computed by using multiple imputations. How do I use these parameter estimates to score new observations and to visualize the model? PROC LOGISTIC can do the computation I want, but how do
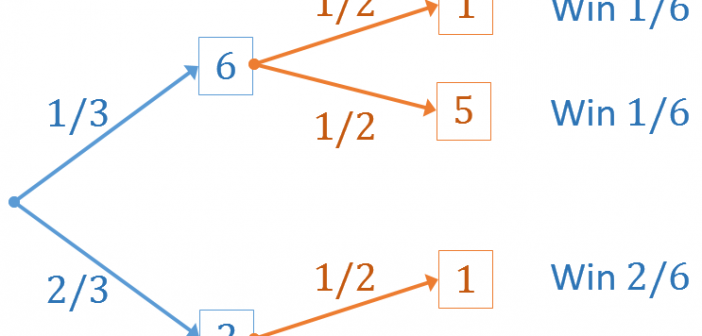
Most games of skill are transitive. If Player A wins against Player B and Player B wins against Player C, then you expect Player A to win against Player C, should they play. Because of this, you can rank the players: A > B > C Interestingly, not all games
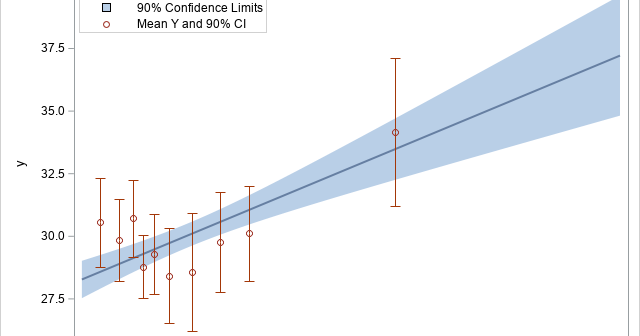
I previously showed how to create a decile calibration plot for a logistic regression model in SAS. A decile calibration plot (or "decile plot," for short) is used in some fields to visualize agreement between the data and a regression model. It can be used to diagnose an incorrectly specified
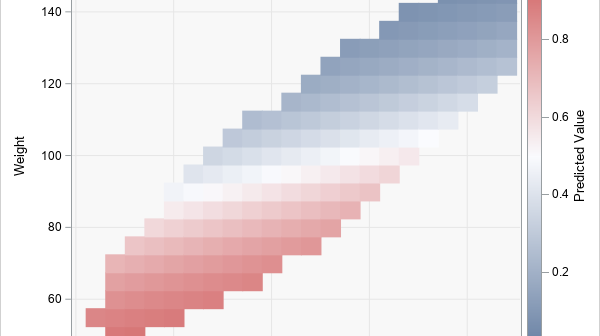
To help visualize regression models, SAS provides the EFFECTPLOT statement in several regression procedures and in PROC PLM, which is a general-purpose procedure for post-fitting analysis of linear models. When scoring and visualizing a model, it is important to use reasonable combinations of the explanatory variables for the visualization. When
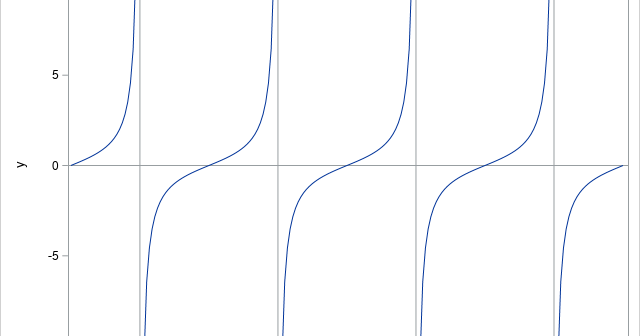
I have previously written about how to plot a discontinuous function in SAS. That article shows how to use the GROUP= option on the SERIES statement to graph a discontinuous function. An alternative approach is to place a missing value for the Y variable at the locations at which the
