The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs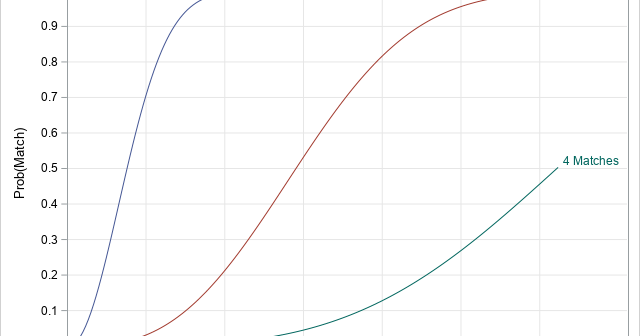
The birthday-matching problem (also called the birthday paradox or simply the birthday problem), is a classic problem in probability. Simply stated, the birthday-matching problem asks, "If there are N people in a room, what is the chance that two of them have the same birthday?" The problem is sometimes called
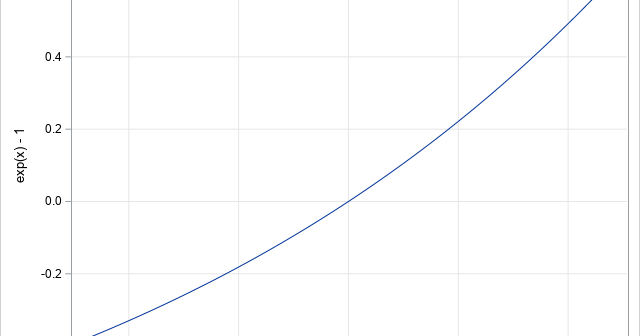
Recently I wrote about numerical analysis problem: the accurate computation of log(1+x) when x is close to 0. A naive computation of log(1+x) loses accuracy if you call the LOG function, which is why the SAS language provides the built-in LOG1PX for this computation. In addition, I showed that you
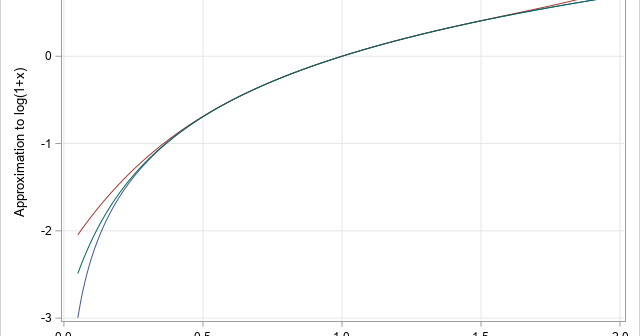
SAS supports a special function for the accurate evaluation of log(1+x) when x is near 0. The LOG1PX function is useful because a naive computation of log(1+x) loses accuracy when x is near 0. This article demonstrates two general approximation techniques that are often used in numerical analysis: the Taylor
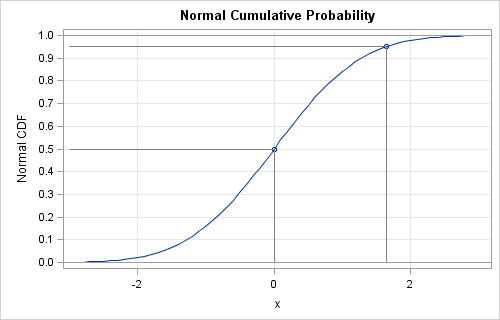
The documentation for Python's SciPy package provides a table that concisely summarizes functions that are associated with continuous probability distributions. This article provides a similar table for SAS functions. For more information on the CDF, PDF, quantile, and random-variate functions, see "Four essential functions for statistical programmers." SAS functions for
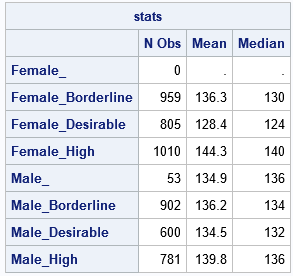
A previous article shows ways to perform efficient BY-group processing in the SAS IML language. BY-group processing is a SAS-ism for what other languages call group processing or subgroup processing. The main idea is that the data set contains several discrete variables such as sex, race, education level, and so

One thing I have learned about rank-based statistics over the years is "Be careful of tied values!" On multiple occasions, I have been asked, "Why doesn't the SAS result for [NAME] statistic agree with my hand calculation?" The answer is sometimes because of the way that tied values are handled.
