The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs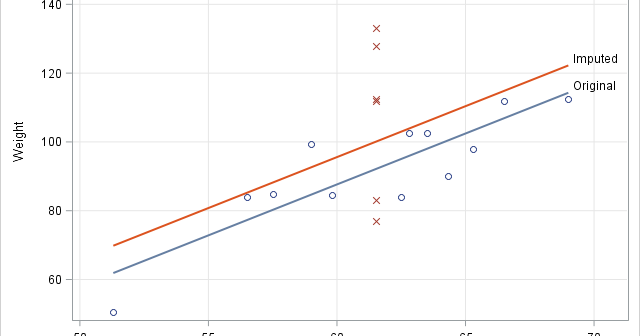
In a previous article, I showed how to use SAS to perform mean imputation. However, there are three problems with using mean-imputed variables in statistical analyses: Mean imputation reduces the variance of the imputed variables. Mean imputation shrinks standard errors, which invalidates most hypothesis tests and the calculation of confidence
Imputing missing data is the act of replacing missing data by nonmissing values. Mean imputation replaces missing data in a numerical variable by the mean value of the nonmissing values. This article shows how to perform mean imputation in SAS. It also presents three statistical drawbacks of mean imputation. How
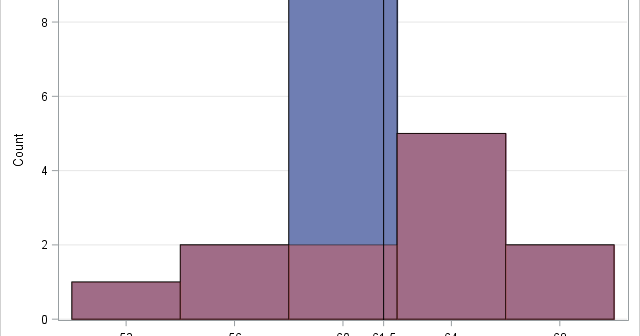
Missing values present challenges for the statistical analyst and data scientist. Many modeling techniques (such as regression) exclude observations that contain missing values, which can reduce the sample size and reduce the power of a statistical analysis. Before you try to deal with missing values in an analysis (for example,
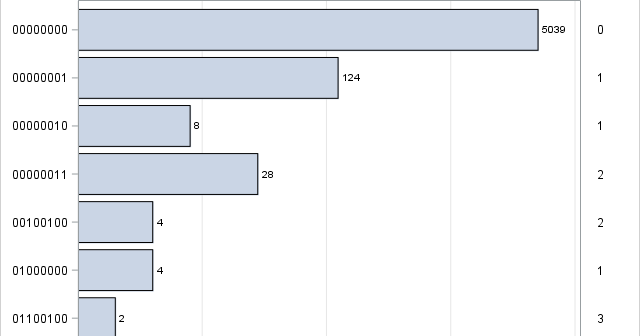
When you run an optimization, it is often not clear how to provide the optimization algorithm with an initial guess for the parameters. A good guess converges quickly to the optimal solution whereas a bad guess might diverge or require many iterations to converge. Many people use a default value
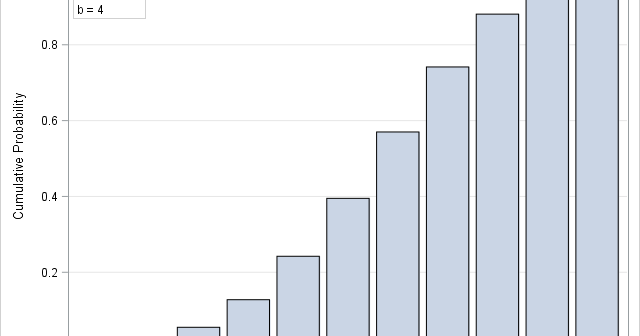
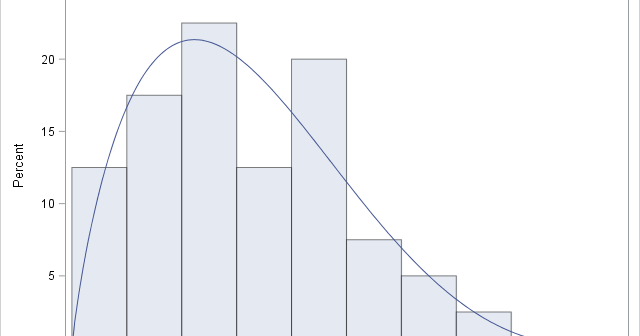
A statistical programmer read my article about the beta-binomial distribution and wanted to know how to compute the cumulative distribution (CDF) and the quantile function for this distribution. In general, if you know the PDF for a discrete distribution, you can also compute the CDF and quantile functions. This article
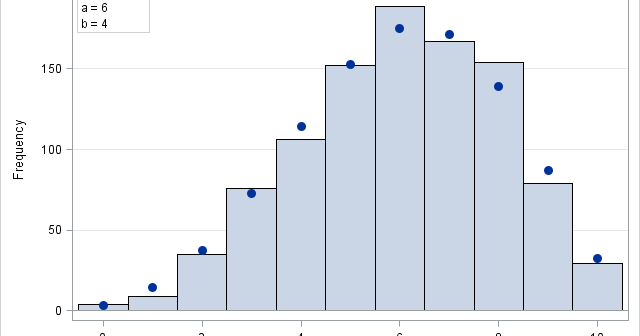
This article shows how to simulate beta-binomial data in SAS and how to compute the density function (PDF). The beta-binomial distribution is a discrete compound distribution. The "binomial" part of the name means that the discrete random variable X follows a binomial distribution with parameters N (number of trials) and
