The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
I wrote more than 100 posts for The DO Loop blog in 2017. The most popular articles were about SAS programming tips, statistical data analysis, and simulation and bootstrap methods. Here are the most popular articles from 2017 in each category. General SAS programming techniques INTCK and INTNX: Do you
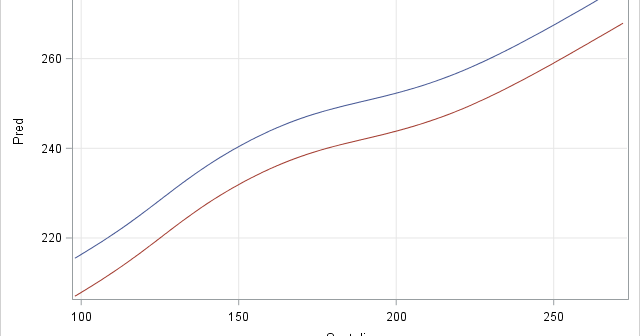
I previously showed an easy way to visualize a regression model that has several continuous explanatory variables: use the SLICEFIT option in the EFFECTPLOT statement in SAS to create a sliced fit plot. The EFFECTPLOT statement is directly supported by the syntax of the GENMOD, LOGISTIC, and ORTHOREG procedures in
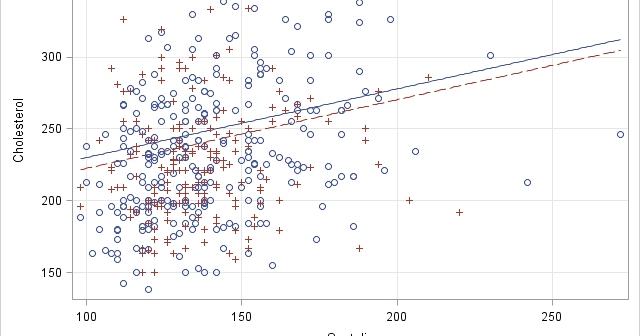
Slice, slice, baby! You've got to slice, slice, baby! When you fit a regression model that has multiple explanatory variables, it is a challenge to effectively visualize the predicted values. This article describes how to visualize the regression model by slicing the explanatory variables. In SAS, you can use the

The SAS language is large. Even after 20+ years of using SAS, there are many features that I have never used. Recently it became necessary for me to learn about DICTIONARY tables in PROC SQL (and the associated SASHELP views) because I needed to programmatically obtain the text for the

Happy holidays to all my readers! My greeting-card to you is an image of a self-similar Christmas tree. The image (click to enlarge) was created in SAS by using two features that I blog about regularly: matrix computations and ODS statistical graphics. Self-similarity in Kronecker products I have previously shown
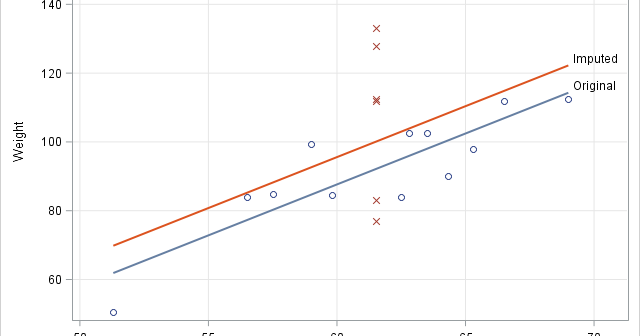
In a previous article, I showed how to use SAS to perform mean imputation. However, there are three problems with using mean-imputed variables in statistical analyses: Mean imputation reduces the variance of the imputed variables. Mean imputation shrinks standard errors, which invalidates most hypothesis tests and the calculation of confidence
