Stellen Sie sich vor, Sie sind frühmorgens mit dem Auto „ab in den Urlaub“ gefahren. Durch vorausschauende Routenplanung sind Sie den größten Staurisiken glücklich ausgewichen und nähern sich bei geschätzten 38°C der letzten Landesgrenze vor Ihrem Urlaubsziel. Die ganze Familie sitzt mit ausgelassener Stimmung im vollgepackten Auto. Die Kinder auf der Rückbank cremen sich schon in Vorfreude auf Strand und Meer mit Sonnenöl ein, während gleichzeitig ein Sonnenhut als Frisbee-Ersatz durch die Fahrerkabine fliegt.

Nun ist die Benzinanzeige am Anfang des „roten Bereiches“, und auf den Vordersitzen wird diskutiert, welche der nächsten Tankstellen angefahren werden soll.

Nehmen wir zu Vereinfachung an, es handelt sich um 17 Tankstellen, die jeweils im Abstand von 10 km auf der verbleibenden Reststrecke liegen und deren Qualität zufällig und unabhängig von ihrer Reihenfolge entlang der Strecke variiert.

Es handelt sich hierbei um ein klassisches Problem der stochastischen Optimierung, bei dem man in einer Situation der ungenauen lokalen Verhältnisse durch zu frühe oder zu späte Entscheidung eventuell unnötig hohe Kosten und Risiken eingeht. Oft divergieren bei dieser Frage auch die Präferenzen und Einschätzungen der Geschlechter, sodass diese Entscheidung zur klassischen Frage des Familienfriedens oder überhaupt des Gelingens eines Urlaubes werden kann …

Zur Lösung des Problems gibt es eine häufig angewendete intuitive und pragmatische Strategie: Man beobachte eine Weile lang in einem vorher festgelegten Beobachtungszeitraum die Tankstellen entlang des Wegs und merke sich deren maximal erreichte Qualität. Dann wähle man im weiteren Verlauf (Selektionszeitraum) die erste Tankstelle zum Tanken aus, deren Qualität die Maximalqualität des Beobachtungszeitraums (Qualitätsschwelle) erreicht oder übertrifft.

Wenn hingegen keine Tankstelle mehr diese Bedingung erfüllt, dann hält man „wohl oder übel“ an der letzten Tankstelle. Bleibt nur noch zu bestimmen, wie man optimalerweise die 17 Tankstellen in Beobachtungszeitraum und Selektionszeitraum aufteilt.

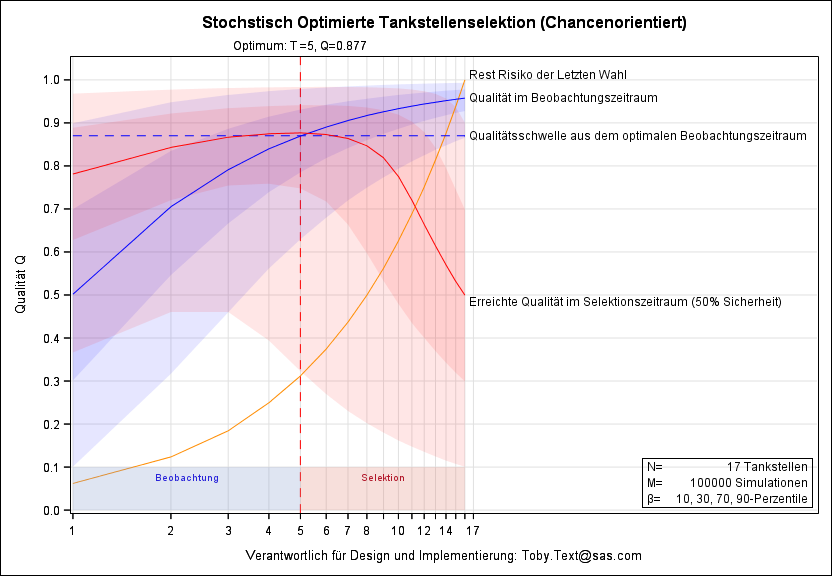
Anbei möchte ich Ihnen eine Lösung mittels stochastischen Optimierung vorstellen, bei der der Median der Qualität (rote Linie) über alle Szenarien, d. h. „risikoneutral“, die Tankstellenqualität im Selektionszeitraum optimiert wird. In diesem Falle sollte man die maximale Qualität Q = 0,87 der ersten 5 Tankstellen als Qualitätsschwelle für den Selektionszeitraum der 6. bis 16. Tankstelle wählen und erreicht damit über alle Szenarien eine Tankstellenqualität von Q = 0,88. Allerdings besteht bei dieser Lösung das Risiko, dass es als Endergebnis in 50 % der Fälle (Simulationen) schlechter als Q = 0,88 ausgehen könnte.

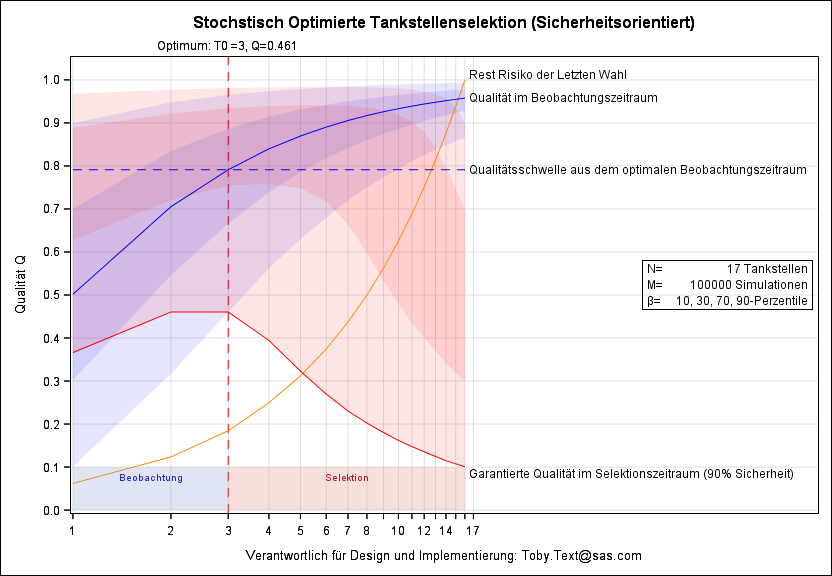
Wenn Sie die 50-%-Garantie eher beunruhigt und Sie mehr auf Sicherheit aus sind, dann beobachten Sie die Qualität nur bis zur dritten Tankstelle T0 = 3. Dort liegt das Maximum des untersten roten 10%-Konfidenzbandes Q = 0,46. Sie erhalten dort aus dem Beobachtungszeitraum eine Qualitätsschwelle von 0,79 für den Selektionszeitraum, mit der Sie dann mit 90 % Wahrscheinlichkeit eine finale Qualität größer oder gleich Q = 0,46 erreichen. Sie sehen, die durch eine frühe Entscheidung erkaufte Sicherheit hat ihren Preis.

Wie kann es nun aber sein, dass bei der sicherheitsorientierten Strategie die zu 90 % garantierte Qualität im Selektionszeitraum so weit unterhalb der Qualitätsschwelle des Beobachtungszeitraumes liegt? Der Sachverhalt klärt sich schnell auf, wenn man die gelbe Linie des „Restrisikos der letzten Wahl“ von P = 18 % an der dritten Tankstelle betrachtet.

Der Fluch des frühen Erfolges

Es besteht das mögliche Dilemma, dass eine frühe Glückssträhne im Beobachtungszeitraum die Qualitätsschwelle für den darauf folgenden Selektionszeitraum so hoch setzt, dass sich in Folge (z.B. nach der Landesgrenze) keine bessere Tankstelle mehr findet, die dieses Kriterium erfüllt. Somit müssen Sie in diesen 18 % aller Fälle „wohl oder übel“ die letzte Tankstelle anfahren mit allen daraus folgenden Konsequenzen, denn ihr Qualitätswert liegt dort rein zufällig zwischen 0 und 1, könnte also auch ziemlich schlecht ausfallen.

Dieses Damoklesschwert der letzten Wahl pendelt von Anfang an über der gesamten Entscheidungsfindung. Es wird mit jeder vorbeiziehenden Tankstelle ein bisschen weiter abgesenkt und sorgt für die schon früher erwähnten Divergenzen bei der Einschätzung durch die Geschlechter auf den Vordersitzen. Hinzu kommt ja noch das hier nicht berücksichtigte Risiko, dass die letzte Tankstelle eventuell gar nicht geöffnet sein könnte …

HIER GEHT'S ZUM SAS CODE, der ganz einfach mit den beschreibenden Statistikprozeduren MEANS und FREQ, SQL und SGPLOT auskommt, den Sie gerne selbst modifizieren (z. B. Anzahl Tankstellen, Anzahl Simulationen) und bei Regenwetter oder Langeweile vom Urlaubsort aus in unseren Cloud Services SAS OnDemand for Academics laufen lassen können.

Übrigens: Ich persönlich empfehle Ihnen unabhängig von diesen Einsichten, jede geöffnete Tankstelle anzufahren, um ein paar Liter zu tanken. Dadurch nutzen Sie den hier nicht behandelten Cost-Averaging-Effekt. Im Zweifelsfall rate ich Ihnen, immer auf Ihren Partner oder Ihre Partnerin einzugehen, wenn es um die Tankstellenwahl geht. Aber bitte lassen Sie den Kopf nicht hängen, wenn Sie dennoch mal auf der Strecke liegen bleiben. Machen Sie das Beste daraus und nutzen Sie die Gelegenheit, um neue exotische Urlaubsbekanntschaften zu machen.

Sie werden sich wundern, wie viele helfende Hände Sie vor Ort finden werden, die Ihnen am Ende aus der Patsche helfen. Mit diesen „Weisheiten” aus meiner „Risk-Practice“ wünsche Ihnen einen ausgelassenen Urlaub. Kommen Sie gut erholt, entspannt und gesund wieder zurück.

Stay tuned

TobyText

P.S. Wenn Ihr Urlaub weniger Abenteurer lieferte als Sie meinen gebucht zu haben, dann sprechen wir hinterher noch mal darüber, wie der Hadoop Elefant Ihre SAS Umgebung anschieben kann. Dann kommen Sie diesbezüglich wenigsten am Arbeitsplatz auf Ihre Kosten – und werden dabei auch noch bezahlt!