The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
Although I do not typically blog about undocumented SAS options, I'll make an exception this time. For many years, I have known that the CONTENTS and COMPARE procedures support the BRIEF and SHORT options, but I always forget which option goes with which procedure. For the record, here are the
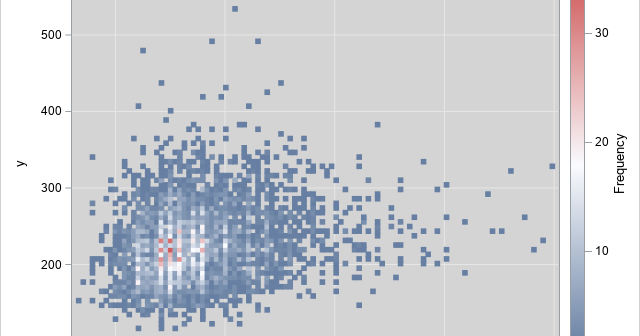
In a scatter plot that displays many points, it can be important to visualize the density of the points. Scatter plots (indeed, all plots that show individual markers) can suffer from overplotting, which means that the graph does not indicate how many observations are at a specific (x, y) location.
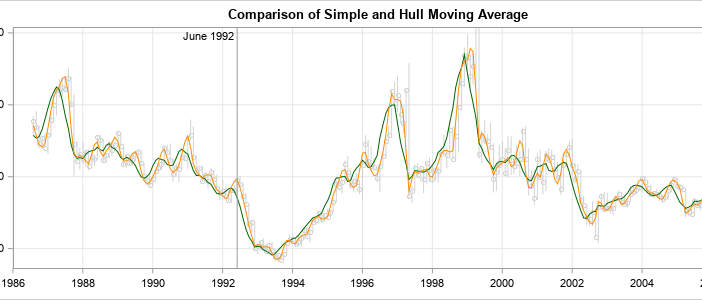
A moving average is a statistical technique that is used to smooth a time series. My colleague, Cindy Wang, wrote an article about the Hull moving average (HMA), which is a time series smoother that is sometimes used as a technical indicator by stock market traders. Cindy showed how to
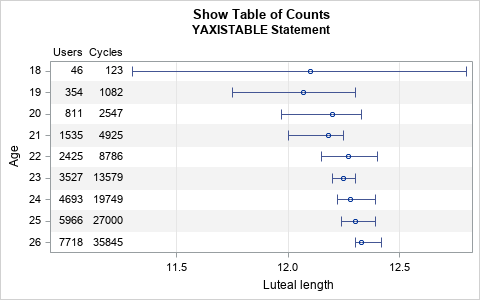
I often use axis tables in PROC SGPLOT in SAS to add a table of text to a graph so that the table values are aligned with the data. But axis tables are not the only way to display tabular data in a graph. You can also use the TEXT
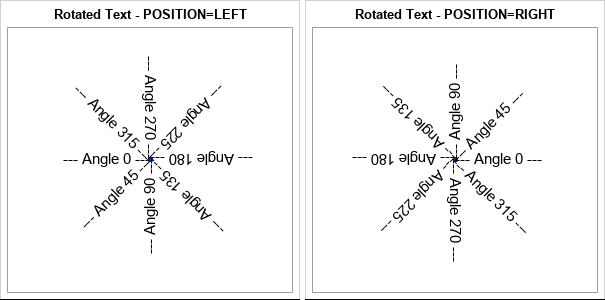
The TEXT statement in PROC SGPLOT supports the ROTATE= option to rotate the specified text. It is worth knowing how the ROTATE= option interacts with the POSITION= option, which determines the anchor point at which the text is positioned. Briefly, the text is positioned FIRST, then the rotation occurs. The
When you order an item online, the website often recommends other items based on your purchase. In fact, these kinds of "recommendation engines" contributed to the early success of companies like Amazon and Netflix. SAS uses a recommender engine to suggest articles on the SAS Support Communities. Although recommender engines
