The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs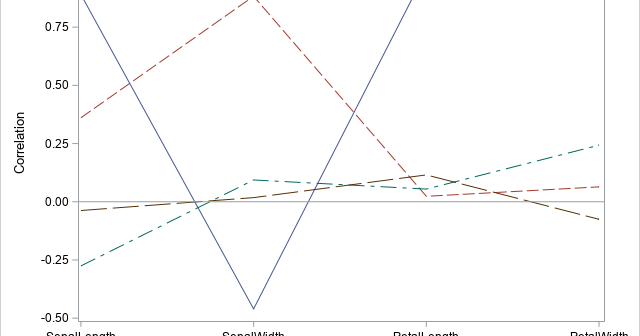
Understanding multivariate statistics requires mastery of high-dimensional geometry and concepts in linear algebra such as matrix factorizations, basis vectors, and linear subspaces. Graphs can help to summarize what a multivariate analysis is telling us about the data. This article looks at four graphs that are often part of a principal

Every year at Halloween, I post an article that shows a SAS trick that is a real treat. This article shows how to use the INTNX function to find dates that are related to a specified date. The INTNX function is a sweet treat, indeed. I previously wrote an article

A common task in SAS programming is to specify a list of variables that satisfy some pattern. You can specify lists for the KEEP= or DROP= data set options, and you can use lists of variables on many SAS statements such as the VAR and MODEL statements. Although SAS has
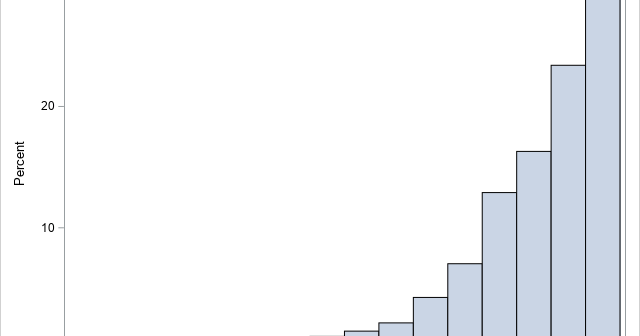
In response to a recent article about how to compute the cosine similarity of observations, a reader asked whether it is practical (or even possible) to perform these types of computations on data sets that have many thousands of observations. The problem is that the cosine similarity matrix is an
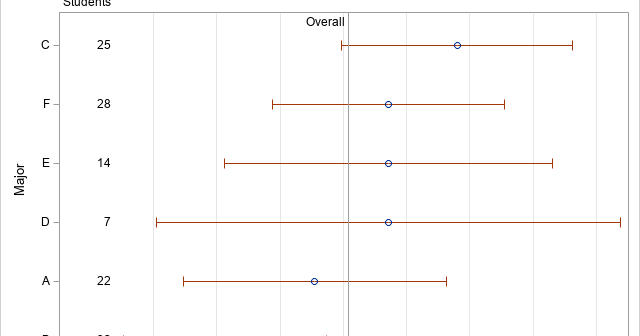
Computing rates and proportions is a common task in data analysis. When you are computing several proportions, it is helpful to visualize how the rates vary among subgroups of the population. Examples of proportions that depend on subgroups include: Mortality rates for various types of cancers Incarceration rates by race
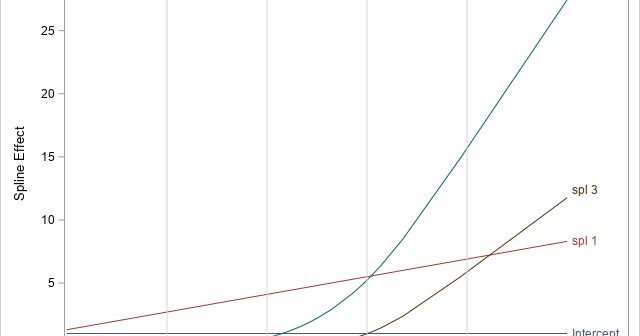
The EFFECT statement is supported by more than a dozen SAS/STAT regression procedures. Among other things, it enables you to generate spline effects that you can use to fit nonlinear relationships in data. Recently there was a discussion on the SAS Support Communities about how to interpret the parameter estimates
