The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs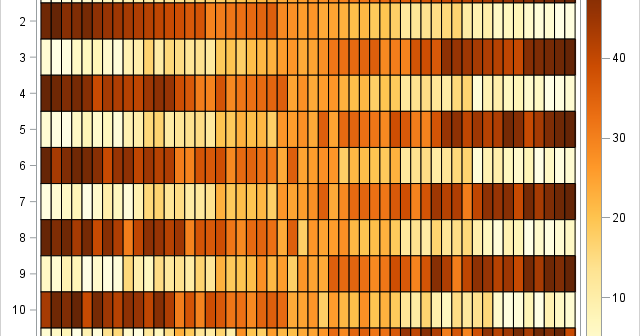
Every day I’m shufflin'. Shufflin', shufflin'. -- "Party Rock Anthem," LMFAO The most popular way to mix a deck of cards is the riffle shuffle, which separates the deck into two pieces and interleaves the cards from each piece. Besides being popular with card players, the riffle shuffle is
The SAS/IML language and the MATLAB language are similar. Both provide a natural syntax for performing high-level computations on vectors and matrices, including basic linear algebra subroutines. Sometimes a SAS programmer will convert an algorithm from MATLAB into SAS/IML. Because the languages are not identical, I am sometimes asked, "what
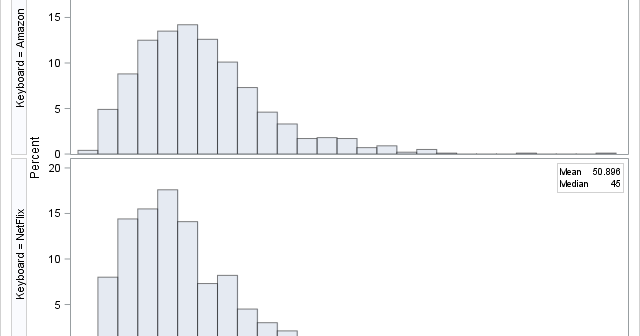
Have you ever tried to type a movie title by using a TV remote control? Both Netflix and Amazon Video provide an interface (a virtual keyboard) that enables you to use the four arrow keys of a standard remote control to type letters. The letters are arranged in a regular

Given a rectangular grid with unit spacing, what is the expected distance between two random vertices, where distance is measured in the L1 metric? (Here "random" means "uniformly at random.") I recently needed this answer for some small grids, such as the one to the right, which is a 7 x 6
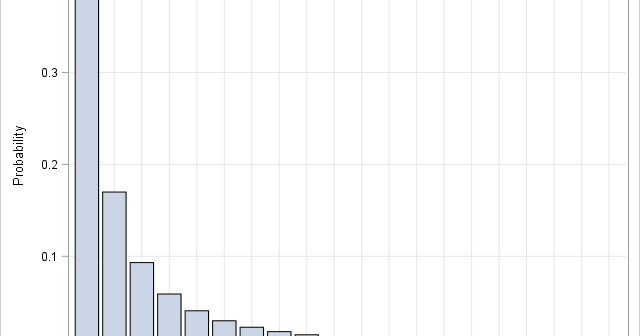
Continued fractions show up in surprising places. They are used in the numerical approximations of certain functions, including the evaluation of the normal cumulative distribution function (normal CDF) for large values of x (El-bolkiny, 1995, p. 75-77) and in approximating the Lambert W function, which has applications in the modeling

In the SAS/IML language, you can only concatenate vectors that have conforming dimensions. For example, to horizontally concatenate two vectors X and Y, the symbols X and Y must have the same number of rows. If not, the statement Z = X || Y will produce an error: ERROR: Matrices
