Sometimes it is important to ensure that a matrix has unique rows. When the data are all numeric, there is an easy way to detect (and delete!) duplicate rows in a matrix.
The main idea is to subtract one row from another. Start with the first row and subtract it from every row beneath it. If any row of the difference matrix is identically zero, then you have found a row that is identical to the first row. Then do the same thing for the second row: subtract it from the third and higher rows and see if you obtain a row of zeros. Repeat this process for the third and higher rows.
The following SAS/IML program implements this algorithm for an arbitrary numeric matrix that contains no missing values. It returns a binary indicator variable (a column vector). The i_th row of the returned vector is 1 for rows that are duplicates of some previous row:
proc iml; /* return binary vector that indicates which rows in a numerical matrix are duplicates. Assumes all values are nonmissing. */ start DupRows(A); N = nrow(A); dupRows = j(N, 1, 0); /* binary indicator matrix */ do i = 1 to N-1; if dupRows[i] = 0 then do; /* skip rows that are known to be duplicates */ r = i+1:N; /* remaining rows */ M = A[r, ]-A[i, ]; /* subtract current row from remaining rows */ b = M[ ,##]; /* sum of squares = 0 iff duplicate row */ idx = loc( b=0 ); /* any duplicate rows for current row? */ if ncol(idx) > 0 then dupRows[r[idx]] = 1; /* if so, flag them */ end; end; return dupRows; finish; |
To test the function, consider the following 6 x 3 matrix. You can see by inspection that the matrix has three duplicate rows: the third, fifth, and sixth rows. You can call the DupRows function and print the matrix adjacent to the binary vector that indicates the duplicate rows:
A = {1 1 1, 1 2 3, 1 1 1, /* duplicate row */ 3 2 1, 3 2 1, /* duplicate row */ 1 1 1}; /* duplicate row */ DupRows = DupRows(A); print A DupRows; |
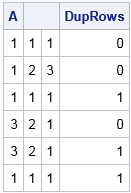
You can use the DupRows function to write a function that excludes the duplicate rows in a matrix and returns only the unique rows, as follows:
/* return the unique rows in a numerical matrix */ start UniqueRows(A); uniqRows = loc(DupRows(A)=0); return(A[uniqRows, ]); /* return rows that are NOT duplicates */ finish; U = UniqueRows(A); print U; |
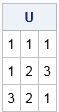
I like this algorithm because it uses subtraction, which is a very fast operation. However, This algorithm has a complexity of O(n(n-1)/2), where n is the number of rows in the matrix, so it is best for small to moderate values of n.
For long and skinny matrices (or for character data), it might be more efficient to sort the matrix as I showed in a previous article about how to find (and count) the unique rows of a matrix. However, the sorting algorithm requires that you sort the data by ALL columns, which can be inefficient for very wide and short data tables. For small and medium-sized data, you can use either method to find the unique rows in a matrix.
The DupRows function is designed for matrices that do not have missing values, as pointed out in a comment by Ian Wakeling. If you might have missing values in your data, use the modified function in the comments, which handles missing values.
This article discusses how to remove duplicates records for numerical matrices in SAS/IML. In Base SAS, you can use PROC SORT or PROC SQL to remove duplicate records from a SAS DATA set, as shown in Lafler (2017) and other references.

4 Comments
Thanks Rick, I think I will make use of this. Should there be a warning or check for missing values? For example the row { . 2 . } could match all sorts of other rows such as {3 2 1} or even {7 . 8}.
Thanks for the comment. You are correct: I designed the algorithm for an application in which there are no missing values (to appear in next Monday's post). As stated, the algorithm will treat missing values as "wildcards" that will match any value, which is probably not what most people want. In particular, if the first row in the matrix contains ALL missing values, the algorithm will flag every row as a "duplicate"! I will edit the post to point out that fact explicitly.
If you want to treat the missing value as a unique value (instead of a wildcard), then I think the simplest modification is to form an indicator matrix for the missing values. You then process not only the numeric data but also the indicator matrix, and you flag a row as a "duplicate" only when the sum of squares of the values AND the sum of squares for the indicators are BOTH zero, as follows:
Rick,
How about this one ?
proc iml;
A = {1 1 1,
1 2 3,
1 1 1, /* duplicate row */
3 2 1,
3 2 1, /* duplicate row */
1 1 1}; /* duplicate row */
flag=j(nrow(A),1);
do i=1 to nrow(A);
temp=repeat(A[i,],nrow(A));
flag[i]=loc((A=temp)[,+]=ncol(A))[1];
end;
idx=unique(flag);
U=A[idx,];
print U;
quit;
Thanks for the alternative. You can speed up your program by eliminating the unnecessary call to REPEAT. Just use
temp=A[i,];