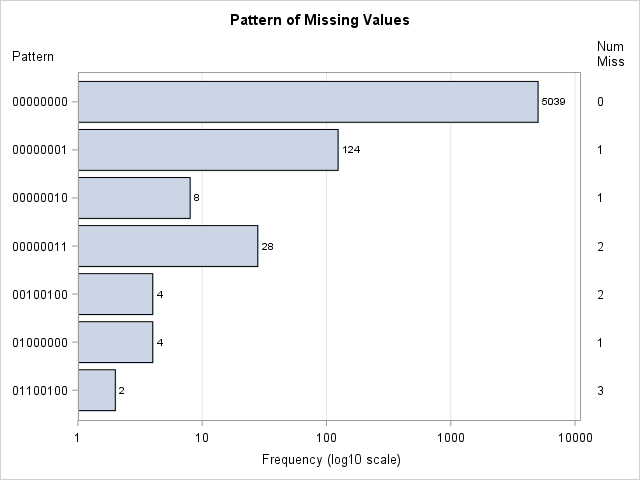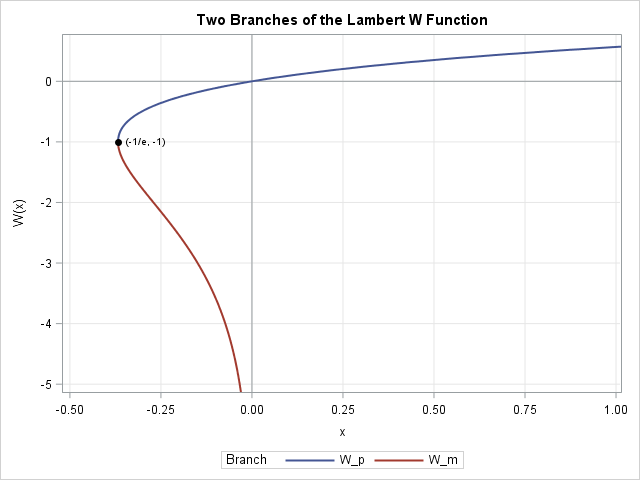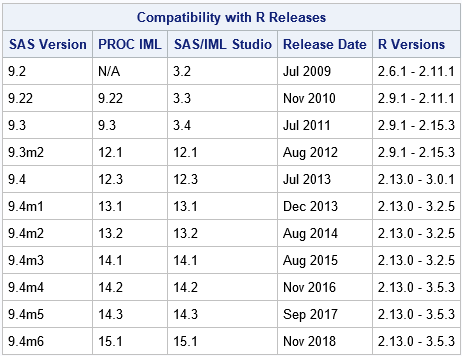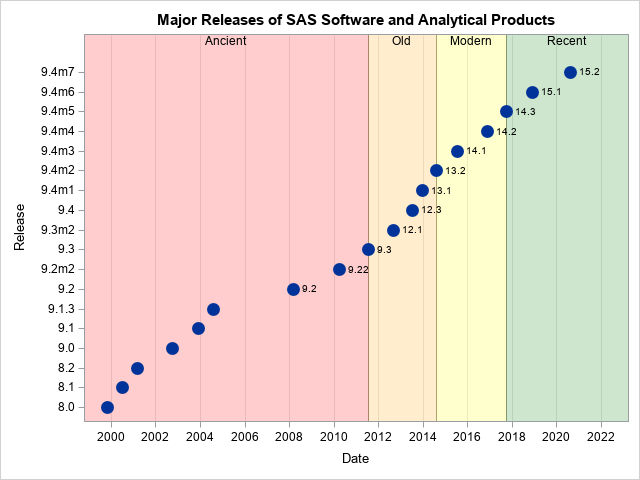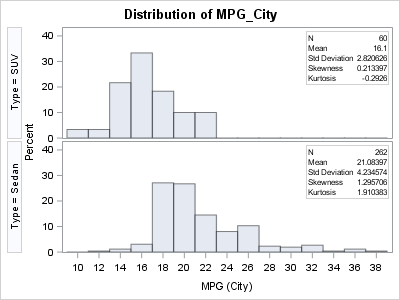
Bootstrap resampling is a powerful way to estimate the standard error for a statistic without making any parametric assumptions about its sampling distribution. The bootstrap method is often implemented by using a sequence of calls to resample from the data, compute a statistic on each sample, and analyze the bootstrap
I recently recorded a short video about the new syntax for specifying and manipulating lists in SAS/IML 14.3. This is a video of my Super Demo at SAS Global Forum 2018. The new syntax supports dynamic arrays, associative arrays ("named lists"), and hierarchical data structures such as lists of lists.
In a previous blog post, I discussed ways to produce statistically independent samples from a random number generator (RNG). The best way is to generate all samples from one stream. However, if your program uses two or more SAS DATA steps to simulate the data, you cannot use the same
