SAS Viyaで線形回帰を行う方法を紹介します。
言語はPythonを使います。
SAS Viyaで線形回帰を行う方法には大きく以下の手法が用意されています。
- 多項回帰: simpleアクションセットで提供。
- 一般化線形回帰または一般線形回帰: regressionアクションセットで提供。
- 機械学習で回帰: 各種機械学習用のアクションセットで提供。
今回は単純なサインカーブを利用して、上記3種類の回帰モデルを作ってみます。
【サインカーブ】
-4≦x<4の範囲でサインカーブを作ります。
普通に \(y = sin(x) \)を算出しても面白みがないので、乱数を加減して以下のようなデータを作りました。これをトレーニングデータとします。
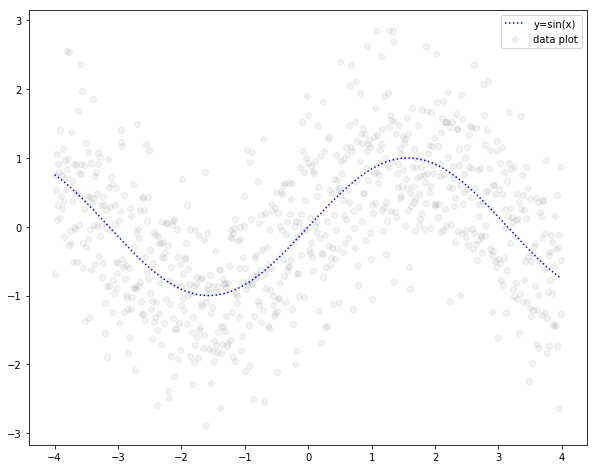
青い点線が \(y=sin(x)\) の曲線、グレーの円は \(y=sin(x)\) に乱数を加減したプロットです。
グレーのプロットの中心を青い点線が通っていることがわかります。
今回はグレーのプロットをトレーニングデータとして線形回帰を行います。グレーのプロットはだいぶ散らばって見えますが、回帰モデルとしては青い点線のように中心を通った曲線が描けるはずです。
トレーニングデータのデータセット名は "sinx" とします。説明変数は "x"、ターゲット変数は "y" になります。
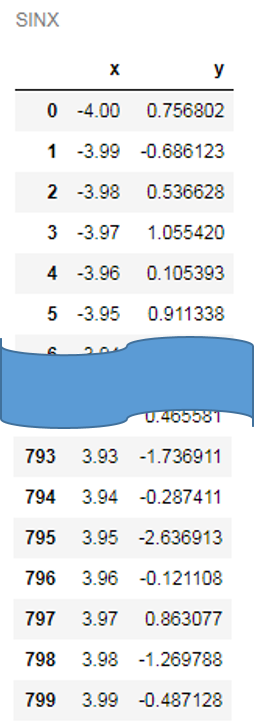
各手法で生成したモデルで回帰を行うため、-4≦x<4 の範囲で0.01刻みで"x" の値をとった "rangex" というデータセットも用意します。

まずはCASセッションを生成し、それぞれのデータをCASにアップロードします。
import swat host = "localhost" port = 5570 user = "cas" password = "p@ssw0rd" mysession = swat.CAS(host, port, user, password) # データをロード dataLoadx = mysession.upload_frame(pdRangex, casout={"name":"rangex", "replace":True}) dataLoadSinx = mysession.upload_frame(pdSinx, casout={"name":"sinx", "replace":True}) |
【多項回帰】
多項回帰にはsimpleアクションセットのregressionアクションを利用します。
プログラムは以下のとおりです。まずは "sinx" データセットを利用して多項回帰を行います。
mysession.loadactionset("simple") # 3項回帰 regSin = mysession.simple.regression( table={"name":"sinx"}, order=3, inputs="x", target="y" ) |
以下のようなテーブルが出力されます。
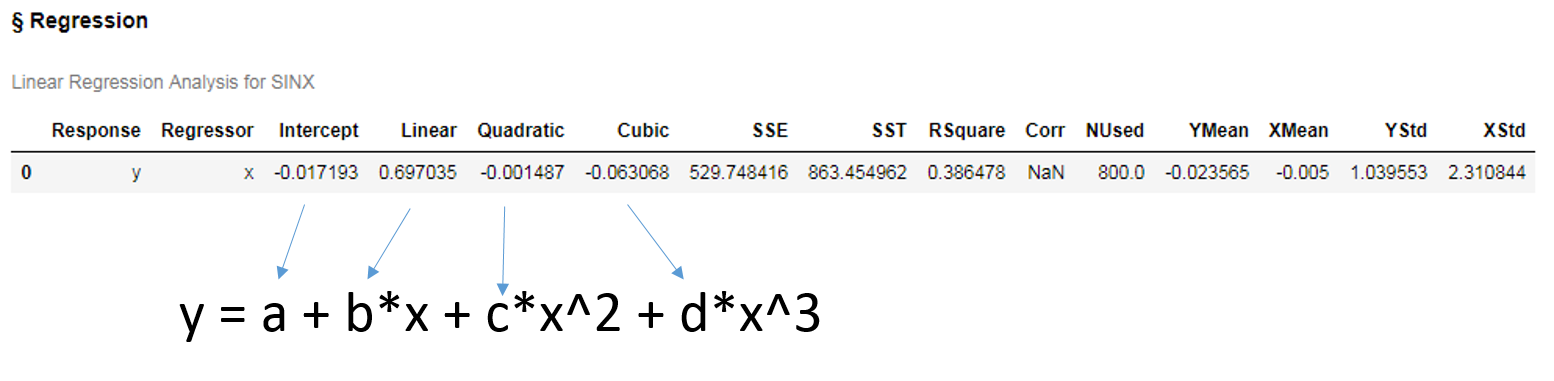
出力値から各項の値がわかりますので、これらを使って "rangex" データセットから y の値を算出し、RMSEを計算してグラフに描画します。
# 予測値として、各xの値について y = a + b*x + c*x^2 + d*x^3 を計算します。 regx = [list(regSin.Regression["Intercept"])[0] + j * list(regSin.Regression["Linear"])[0]+ (j ** 2) * list(regSin.Regression["Quadratic"])[0] + (j ** 3) * list(regSin.Regression["Cubic"])[0] for j in list(x)] regxy = pd.DataFrame(np.vstack((x, np.array(regx))).T, columns=["x","y"]) # グレーのプロットに対するRMSE regRMSE = RMSE(pdSinx, regxy) # グラフに描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(regxy["x"], regxy["y"], label="Reg, {0}".format(regRMSE), color="orange") plt.legend() plt.show() |
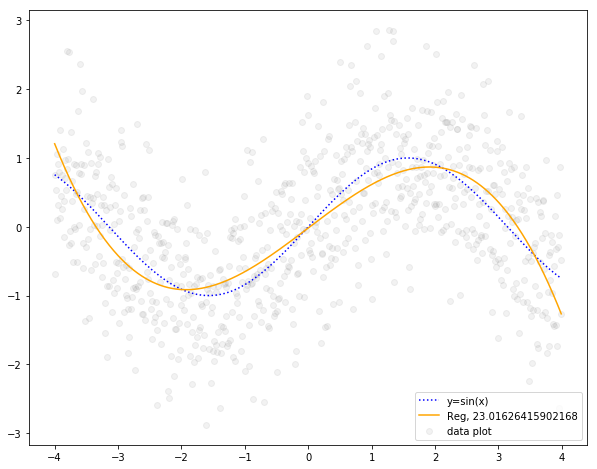
オレンジの実線が多項回帰の結果です。青い点線がサインカーブ、グレーのプロットがトレーニングデータです。
オレンジの実線が青い点線と多少ずれていることがわかります。グレーのプロットに対するRMSEは23.016...とのことで、まだ改善の余地がありそうです。
【一般化線形回帰】
続いて一般化線形回帰を行います。プログラムは以下のとおりです。
mysession.loadactionset(actionset='regression') # 一般化線形回帰 glmSin = mysession.regression.glm( table={"name":"sinx"}, model={ "depVar":"y", "effects":"sptemp" }, spline=[{ # splineで曲線化 "name":"sptemp", "naturalCubic":True, "vars":{"x"} }], code={ "comment":True } ) |
一般化線形回帰を行う場合、スプライン(spline)オプションを用いることで曲線を表現することができます。
regressionアクションセットではcodeオプションを指定することで、回帰モデルをsasコードとして出力することができます。
例として以下のようなコード(抜粋)となっており、SAS Datastepに組み込んで利用することが可能です。
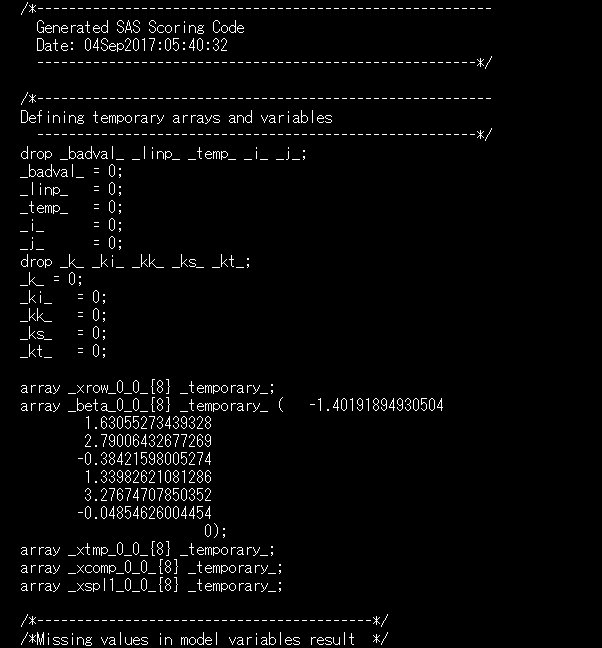
今回はこのコードをSAS Datastepに組み込んで "rangex" から "y" を算出する関数として dsScoring() を定義して使います(dsScoring() 関数の内容は本ブログ末尾に記載しています)。
# xの値から一般化線形回帰で曲線の値を算出 dsScoring(caslib="casuser", codeDF=glmSin._code_, inputData="rangex", outputDF="glmScored") glmxy = pd.DataFrame(mysession.CASTable("glmScored").head(n=len(mysession.CASTable("glmScored")))) # グレーのプロットに対するRMSEを算出 glmRMSE = RMSE(pdSinx, glmxy) # グラフを描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(glmxy["x"], glmxy["P_y"], label="Glm, {0}".format(glmRMSE), color="green") plt.legend() plt.show() |
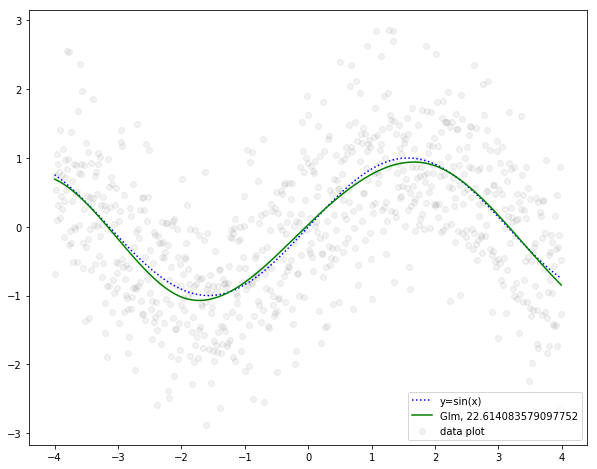
緑の曲線が一般化線形回帰の結果です。青い点線のサインカーブとだいぶ重なるようになりました。グレーのプロットに対するRMSEが22.614...とのことで、多項回帰よりも改善されていることがわかります。
【ランダムフォレスト】
最後にランダムフォレストで線形回帰を試してみたいと思います。
ランダムフォレストはツリーモデルの一種なので、曲線を曲線として予測することはできません。ランダムフォレストで予測した曲線は段階的なかくかくした形になります。
プログラムは以下になります。
mysession.loadactionset("decisionTree") # ランダムフォレストで回帰 rfSin = mysession.decisionTree.forestTrain( table= {'name':'sinx'}, target = "y", inputs = {"x"}, savestate = {"name":"savestate", "replace":True} # savestateで予測モデルを生成 ) |
ランダムフォレストの予測モデルはsavestateオプションでバイナリ形式のデータセットとして出力することができます。上記では "savestate" というデータセットを出力しています。savestateのバイナリデータはastoreアクションセットのscoreアクションで呼び出し、予測を行うことができます。
# ランダムフォレスト予測モデルでxの値から曲線の値を算出 mysession.loadactionset('aStore') atscore = mysession.score( table={'name':'rangex'}, out='scored', rstore='savestate' ) rfxy = pd.DataFrame(mysession.CASTable('scored').head(n=len(mysession.CASTable('scored')))) rfxy = pd.concat([pdRangex, rfxy], axis=1) # RMSEを算出 rfRMSE = RMSE(pdSinx, rfxy) # グラフを描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(rfxy["x"], rfxy["P_y"], label="RandomForest, {0}".format(rfRMSE), color="red") plt.legend() plt.show() |
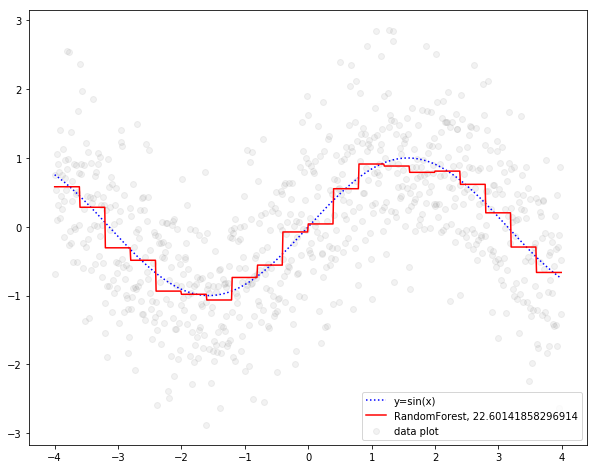
階段形式の赤い線がランダムフォレストの結果です。ツリーモデルのため、曲線にはなりません。青い点線のサインカーブとおおむね重なっているようにみえます。RMSEは22.601...で、一般化線形回帰よりもすこし良い結果になっています。
最後にすべての回帰線を1つのグラフにまとめます。
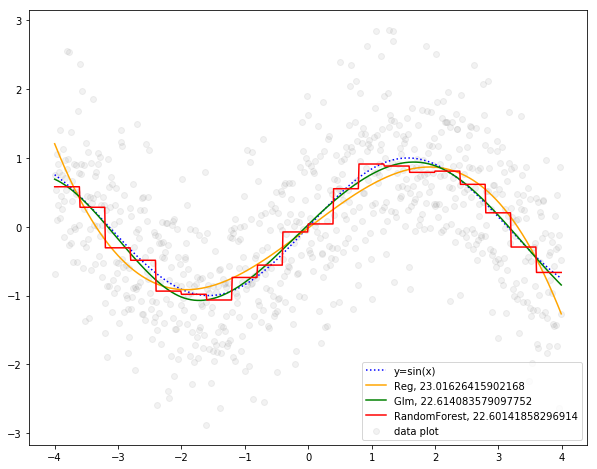
実線が予測線、点線がサインカーブ、グレーのプロットがトレーニングデータです。いずれの予測線もグレーのプロットの中心あたりを通っていることがわかります。
【おまけ】
今回作ったプログラムです。
# pythonでSAS Datastepを実行して予測を行う関数 def dsScoring(caslib, codeDF, inputData, outputDF, tmpCode="/tmp/testcode.csv", saveCode=False): mysession.loadactionset("dataStep") import pandas as pd pdCode = pd.DataFrame(codeDF) strCode = "" for i in range(len(pdCode)): strCode = strCode + pdCode.iloc[i,0] dstep = "data {caslib}.{outputDF}; set {caslib}.{inputData}; {strCode} run;".format(caslib=caslib, outputDF=outputDF, inputData=inputData, strCode=strCode) glmSolScore = mysession.dataStep.runcode( code = dstep ) if saveCode == True: codeDF.to_csv(tmpCode, index=False, header=False) # RMSEを算出する関数 def RMSE(realData, inferData): import math sumDif = 0 for i in range(len(realData)): sumDif += math.pow((realData.iloc[i,1] - inferData.iloc[i,1]), 2) return math.sqrt(sumDif) # サインカーブとトレーニングデータを生成 import numpy as np import matplotlib.pyplot as plt import pandas as pd # 4≦x<4の範囲で0.01刻みでxの配列を生成 x = np.arange(-4, 4, 0.01) pdRangex = pd.DataFrame(x, columns=["x"]) # sin(x)を算出 sinx = np.sin(x) # 乱数を加減したトレーニングデータを生成 y = np.sin(x[0]) for i in range(len(x)-1): fl = np.random.rand() if fl < 0.15: ran = (np.sin(x[i+1])+(np.random.rand() * 2)) elif fl > 0.85: ran = (np.sin(x[i+1])-(np.random.rand() * 2)) else: if i % 2 == 0: ran = (np.sin(x[i+1]))+(np.random.rand()) else: ran = (np.sin(x[i+1]))-(np.random.rand()) y = np.hstack((y, ran)) sin = np.vstack((x, y)).T pdSinx = pd.DataFrame(sin, columns=["x","y"]) # グラフに描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.legend() plt.show() # CASセッションを生成し、データをロード import swat host = "localhost" port = 5570 user = "cas" password = "p@ssw0rd" mysession = swat.CAS(host, port, user, password) dataLoadx = mysession.upload_frame(pdRangex, casout={"name":"rangex", "replace":True}) dataLoadSinx = mysession.upload_frame(pdSinx, casout={"name":"sinx", "replace":True}) # 多項回帰 mysession.loadactionset("simple") # 3項回帰 regSin = mysession.simple.regression( table={"name":"sinx"}, order=3, inputs="x", target="y" ) # 予測値として、各xの値について y = a + b*x + c*x^2 + d*x^3 を計算します。 regx = [list(regSin.Regression["Intercept"])[0] + j * list(regSin.Regression["Linear"])[0]+ (j ** 2) * list(regSin.Regression["Quadratic"])[0] + (j ** 3) * list(regSin.Regression["Cubic"])[0] for j in list(x)] regxy = pd.DataFrame(np.vstack((x, np.array(regx))).T, columns=["x","y"]) # RMSEを算出します。 regRMSE = RMSE(pdSinx, regxy) # グラフを描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(regxy["x"], regxy["y"], label="Reg, {0}".format(regRMSE), color="orange") plt.legend() plt.show() mysession.loadactionset(actionset='regression') # 一般化線形回帰 glmSin = mysession.regression.glm( table={"name":"sinx"}, model={ "depVar":"y", "effects":"sptemp" }, spline=[{ # splineで曲線化 "name":"sptemp", "naturalCubic":True, "vars":{"x"} }], code={ "comment":True } ) # xの値から一般化線形回帰で曲線の値を算出 dsScoring(caslib="casuser", codeDF=glmSin._code_, inputData="rangex", outputDF="glmScored") glmxy = pd.DataFrame(mysession.CASTable("glmScored").head(n=len(mysession.CASTable("glmScored")))) # RMSEを算出 glmRMSE = RMSE(pdSinx, glmxy) # グラフを描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(glmxy["x"], glmxy["P_y"], label="Glm, {0}".format(glmRMSE), color="green") plt.legend() plt.show() mysession.loadactionset("decisionTree") # ランダムフォレストで回帰 rfSin = mysession.decisionTree.forestTrain( table= {'name':'sinx'}, target = "y", inputs = {"x"}, savestate = {"name":"savestate", "replace":True} # savestateで予測モデルを生成 ) # ランダムフォレスト予測モデルでxの値から曲線の値を算出 mysession.loadactionset('aStore') atscore = mysession.score( table={'name':'rangex'}, out='scored', rstore='savestate' ) rfxy = pd.DataFrame(mysession.CASTable('scored').head(n=len(mysession.CASTable('scored')))) rfxy = pd.concat([pdRangex, rfxy], axis=1) # RMSEを算出 rfRMSE = RMSE(pdSinx, rfxy) # グラフを描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(rfxy["x"], rfxy["P_y"], label="RandomForest, {0}".format(rfRMSE), color="red") plt.legend() plt.show() # まとめてグラフに描画 fig = plt.figure(figsize=(10,8)) plt.scatter(x, y, alpha=0.1, color="gray", label="data plot") plt.plot(x, sinx, label="y=sin(x)", color="blue", linestyle="dotted") plt.plot(regxy["x"], regxy["y"], label="Reg, {0}".format(regRMSE), color="orange") plt.plot(glmxy["x"], glmxy["P_y"], label="Glm, {0}".format(glmRMSE), color="green") plt.plot(rfxy["x"], rfxy["P_y"], label="RandomForest, {0}".format(rfRMSE), color="red") plt.legend() plt.show() |
