The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
In categorical data analysis, it is common to analyze tables of counts. For example, a researcher might gather data for 18 boys and 12 girls who apply for a summer enrichment program. The researcher might be interested in whether the proportion of boys that are admitted is different from the
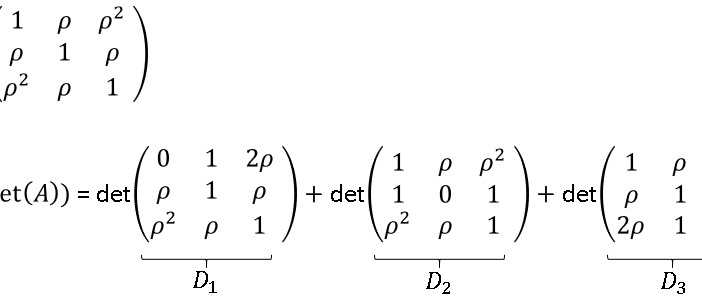
Did you know that there is a mathematical formula that simplifies finding the derivative of a determinant? You can compute the derivative of a determinant of an n x n matrix by using the sum of n other determinants. The n determinants are for matrices that are equal to the original matrix
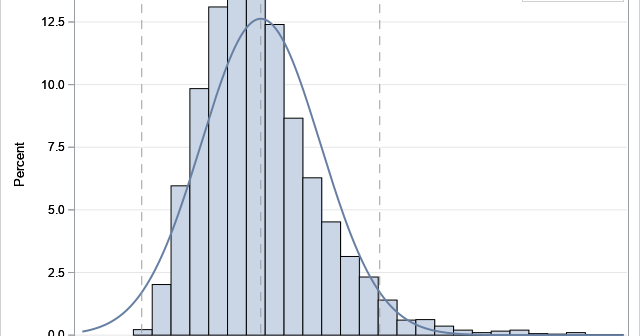
In The Essential Guide to Bootstrapping in SAS, I note that there are many SAS procedures that support bootstrap estimates without requiring the analyst to write a program. I have previously written about using bootstrap options in the TTEST procedure. This article discusses the NLIN procedure, which can fit nonlinear
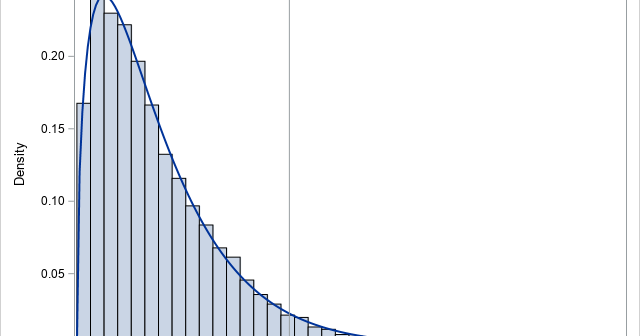
Recently, I wrote about Bartlett's test for sphericity. The purpose of this hypothesis test is to determine whether the variables in the data are uncorrelated. It works by testing whether the sample correlation matrix is close to the identity matrix. Often statistics textbooks or articles include a statement such as

When you have many correlated variables, principal component analysis (PCA) is a classical technique to reduce the dimensionality of the problem. The PCA finds a smaller dimensional linear subspace that explains most of the variability in the data. There are many statistical tools that help you decide how many principal
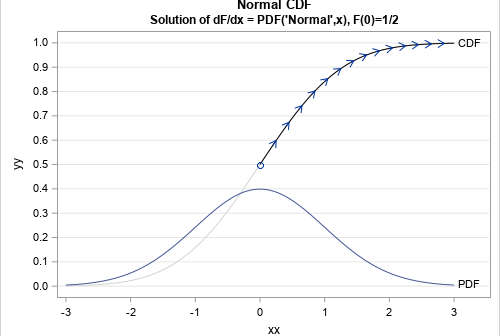
To a numerical analyst, numerical integration has two meanings. Numerical integration often means solving a definite integral such as \(\int_{a}^b f(s) \, ds\). Numerical integration is also called quadrature because it computes areas. The other meaning applies to solving ordinary differential equations (ODEs). My article about new methods for solving
