The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
A SAS programmer asked how to display long labels at irregular locations along the horizontal axis of scatter plot. The labels indicate various phases of a clinical study. This article discusses the problem and shows how to use the FITPOLICY=STAGGER option on the XAXIS or X2AXIS statement to avoid collisions
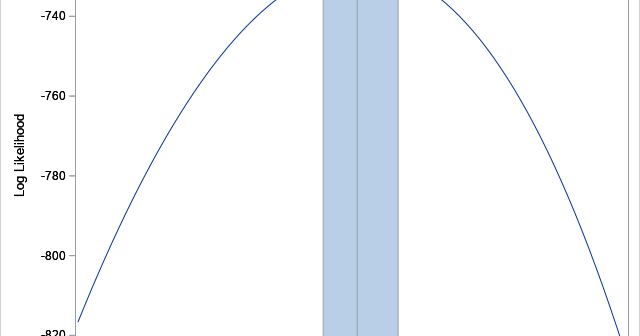
A SAS customer asked how to use the Box-Cox transformation to normalize a single variable. Recall that a normalizing transformation is a function that attempts to convert a set of data to be as nearly normal as possible. For positive-valued data, introductory statistics courses often mention the log transformation or
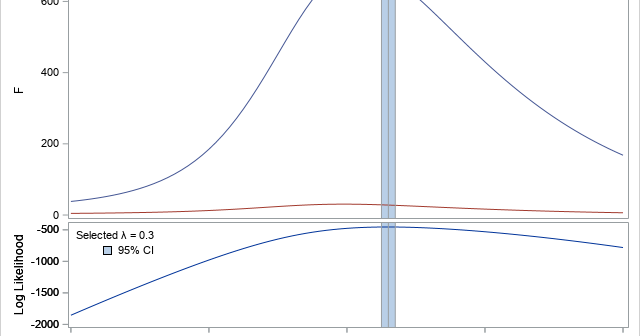
In the 1960s and '70s, before nonparametric regression methods became widely available, it was common to apply a nonlinear transformation to the dependent variable before fitting a linear regression model. This is still done today, with the most common transformation being a logarithmic transformation of the dependent variable, which fits
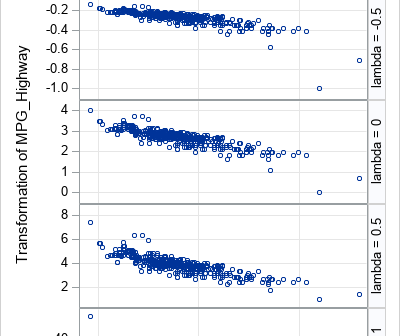
John Tukey was an influential statistician who proposed many statistical concepts. In the 1960s and 70s, he was fundamental in the discovery and exposition of robust statistical methods, and he was an ardent proponent of exploratory data analysis (EDA). In his 1977 book, Exploratory Data Analysis, he discussed a small
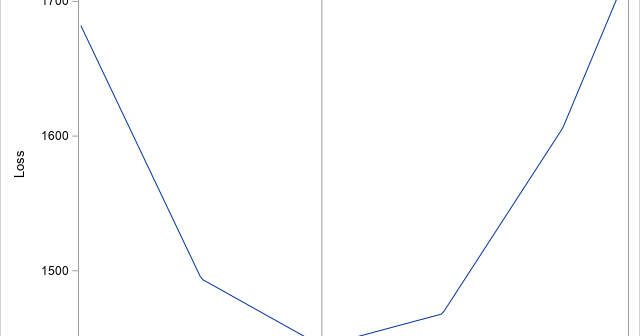
On Twitter, I saw a tweet from @DataSciFact that read, "The sum of (x_i - x)^2 over a set of data points x_i is minimized when x is the sample mean." I (@RickWicklin) immediately tweeted out a reply: "And the sum of |x_i - x| is minimized by the sample

A SAS programmer asked for help on a discussion forum: "My SAS session will not display any tables or graphs! I try to use PROC PRINT and other procedures, but no output is displayed! What can I do?" The most common reasons why you might not see any output when
