The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs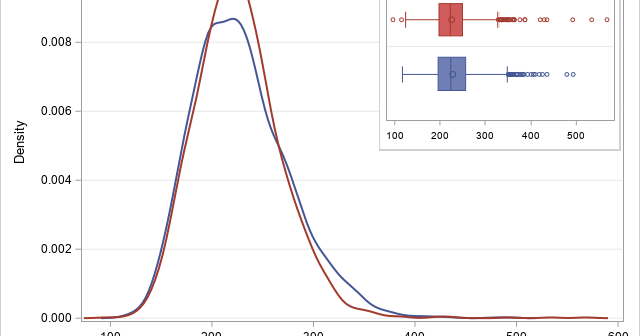
In a previous article, I presented some of the most popular blog posts from 2023. The popular articles tend to discuss elementary topics that have broad appeal. However, I also wrote many technical articles about advanced topics. The following articles didn't make the Top 10 list, but they deserve a
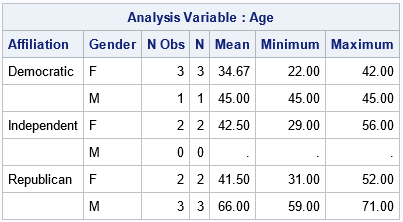
An unobserved category is one that does not appear in a sample of data. For example, in a small sample of US voters, you are likely to observe members of the major political parties, but less likely to observe members of minor or fringe parties. This can cause a headache
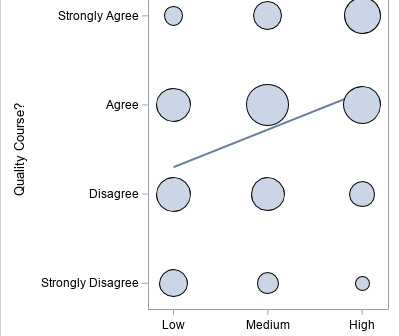
In 2023, I wrote 90 articles for The DO Loop blog. My most popular articles were about SAS programming, data visualization, and statistics. In addition, several "general interest" articles were popular, including my article for Pi Day and an article about AI chatbots. If you missed any of these articles,
Statistical software often includes supports for a weight variable. Many SAS procedures make a distinction between integer frequencies and more general "importance weights." Frequencies are supported by using the FREQ statement in SAS procedures; general weights are supported by using the WEIGHT statement. An exception is PROC FREQ, which contains
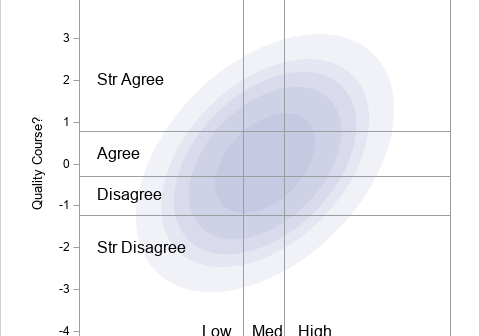
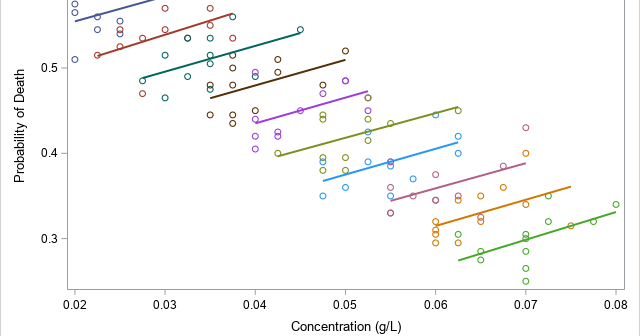
SAS provides many built-in routines for data analysis. A previous article discusses polychoric correlation, which is a measure of association between two ordinal variables. In SAS, you can use PROC FREQ or PROC CORR to estimate the polychoric correlation, its standard error, and confidence intervals. Although SAS provides a built-in
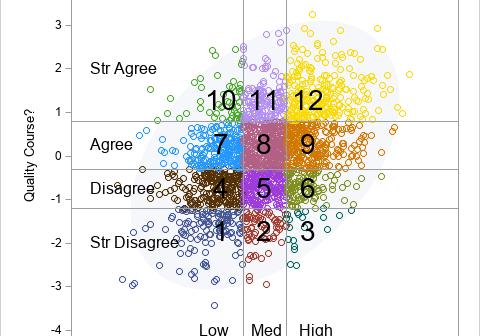
Correlation is a statistic that measures the association between two variables. When two variables are positively correlated, low values of one variable tend to be associated with low values of the other variable. Medium values and high values are similarly associated. For negative correlation, the association is flipped: low values
