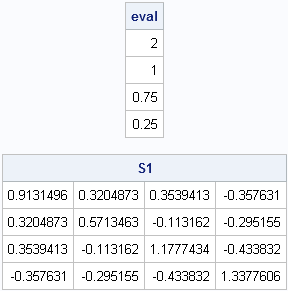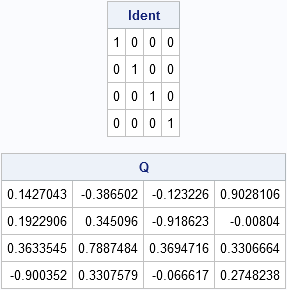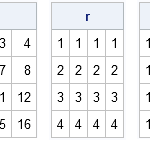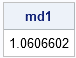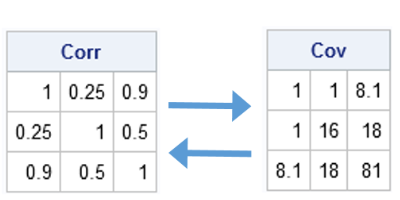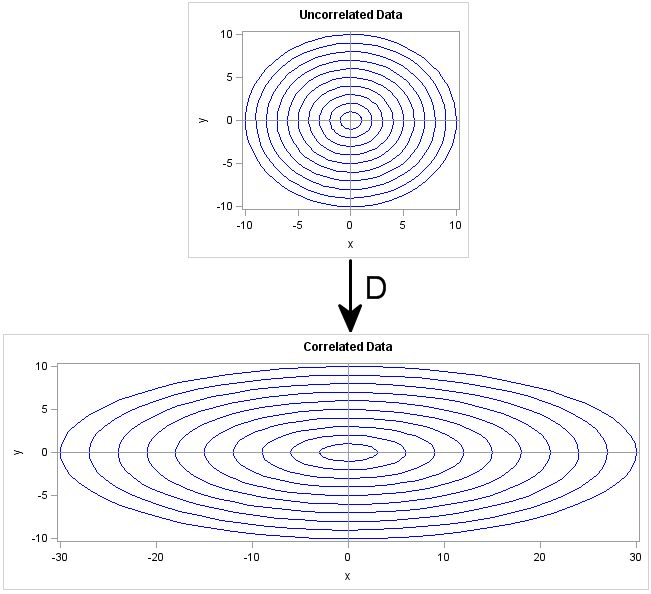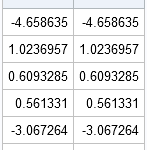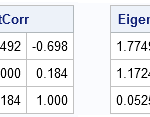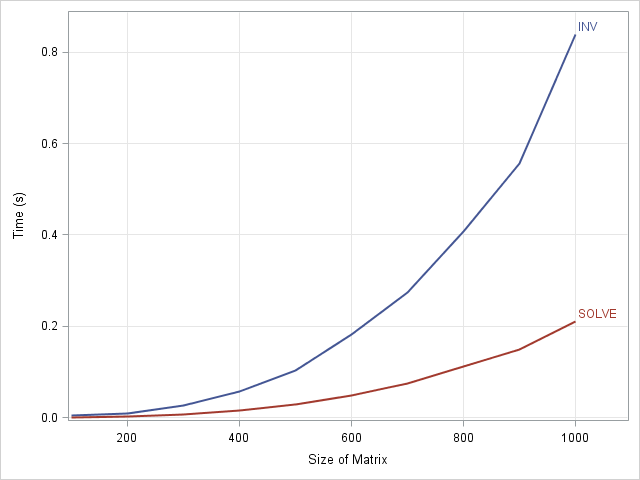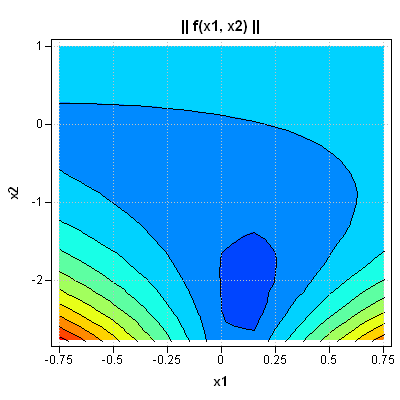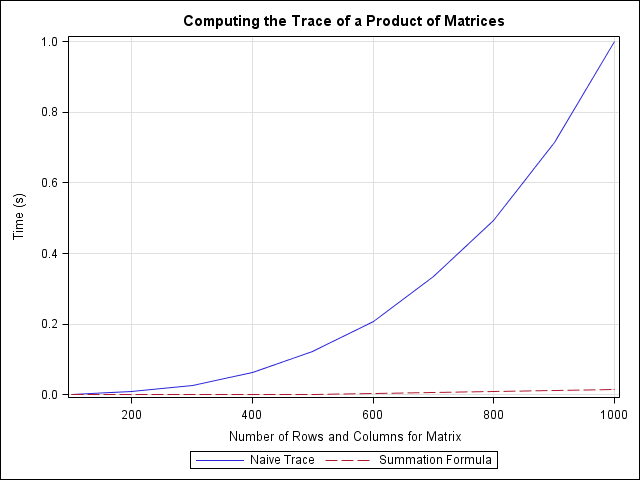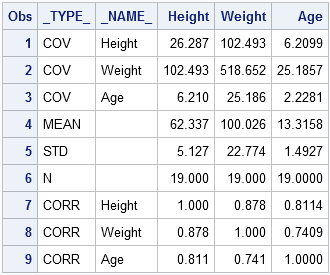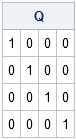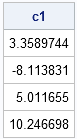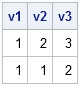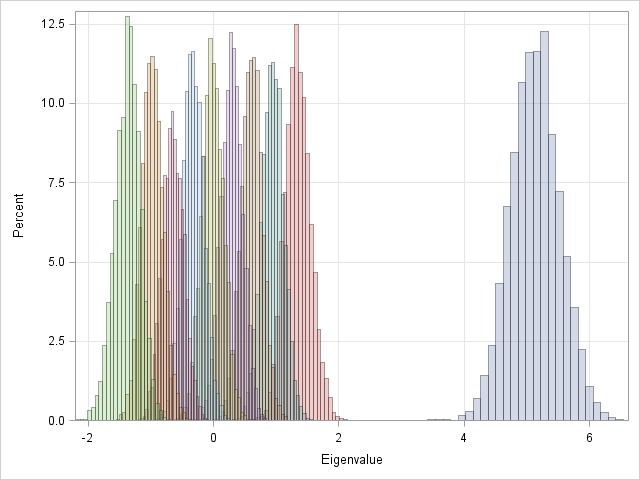
I've been a fan of statistical simulation and other kinds of computer experimentation for many years. For me, simulation is a good way to understand how the world of statistics works, and to formulate and test conjectures. Last week, while investigating the efficiency of the power method for finding dominant
When I was at SAS Global Forum last week, a SAS user asked my advice regarding a SAS/IML program that he wrote. One step of the program was taking too long to run and he wondered if I could suggest a way to speed it up. The long-running step was
In a previous post I showed how to implement Stewart's (1980) algorithm for generating random orthogonal matrices in SAS/IML software. By using the algorithm, it is easy to generate a random matrix that contains a specified set of eigenvalues. If D = diag(λ1, ..., λp) is a diagonal matrix and
Because I am writing a new book about simulating data in SAS, I have been doing a lot of reading and research about how to simulate various quantities. Random integers? Check! Random univariate samples? Check! Random multivariate samples? Check! Recently I've been researching how to generate random matrices. I've blogged
Sometimes in matrix computations you need to obtain the values of certain submatrices such as the diagonal elements or the super- or subdiagonal elements. About a year ago, I showed one way to do that: convert subscripts to indices and vice-versa. However, a tip from @RLangTip on Twitter got me
I recently blogged about Mahalanobis distance and what it means geometrically. I also previously showed how Mahalanobis distance can be used to compute outliers in multivariate data. But how do you compute Mahalanobis distance in SAS? Computing Mahalanobis distance with built-in SAS procedures and functions There are several ways to
I have previously blogged about how to convert a covariance matrix into a correlation matrix in SAS (and the other way around). However, I still get questions about it, perhaps because my previous post demonstrated more than one way to accomplish each transformation. To eliminate all confusion, the following SAS/IML
A variance-covariance matrix expresses linear relationships between variables. Given the covariances between variables, did you know that you can write down an invertible linear transformation that "uncorrelates" the variables? Conversely, you can transform a set of uncorrelated variables into variables with given covariances. The transformation that works this magic is
Once again I rediscovered something that I once knew, but had forgotten. Fortunately, this blog is a good place to share little code snippets that I don't want to forget. I needed to compute the diagonal elements of a product of two matrices. In symbols, I have an nxp matrix,
It is "well known" that the pairwise deletion of missing values and the resulting computation of correlations can lead to problems in statistical computing. I have previously written about this phenomenon in my article "When is a correlation matrix not a correlation matrix." Specifically, consider the symmetric array whose elements
Birds migrate south in the fall. Squirrels gather nuts. Humans also have behavioral rituals in the autumn. I change the batteries in my smoke detectors, I switch my clocks back to daylight standard time, and I turn the mattress on my bed. The first two are relatively easy. There's even
I've previously described ways to solve systems of linear equations, A*b = c. While discussing the relative merits of the solving a system for a particular right hand side versus solving for the inverse matrix, I made the assertion that it is faster to solve a particular system than it
The SAS/IML language provides two functions for solving a nonsingular nxn linear system A*x = c: The INV function numerically computes the inverse matrix, A-1. You can use this to solve for x: Ainv = inv(A); x = Ainv*c;. The SOLVE function numerically computes the particular solution, x, for a
I've previously discussed how to find the root of a univariate function. This article describes how to find the root (zero) of a function of several variables by using Newton's method. There have been many papers, books, and dissertations written on the topic of root-finding, so why am I blogging
Recently I had to compute the trace of a product of square matrices. That is, I had two large nxn matrices, A and B, and I needed to compute the quantity trace(A*B). Furthermore, I was going to compute this quantity thousands of times for various A and B as part
Both covariance matrices and correlation matrices are used frequently in multivariate statistics. You can easily compute covariance and correlation matrices from data by using SAS software. However, sometimes you are given a covariance matrix, but your numerical technique requires a correlation matrix. Other times you are given a correlation matrix,
Sample covariance matrices and correlation matrices are used frequently in multivariate statistics. This post shows how to compute these matrices in SAS and use them in a SAS/IML program. There are two ways to compute these matrices: Compute the covariance and correlation with PROC CORR and read the results into
The SAS/IML language enables you to perform matrix-vector computations. However, it also provides a convenient "shorthand notation" that enables you to perform elementwise operation on rows or columns in a natural way. You might know that the SAS/IML language supports subscript reduction operators to compute basic rowwise or columnwise quantities.
In a previous post, I discussed computing regression coefficients in different polynomial bases and showed how the coefficients change when you change the basis functions. In particular, I showed how to convert the coefficients computed in one basis to coefficients computed with respect to a different basis. It turns out
I am pleased to announce that the fine folks at SAS Press have made Chapter 2 of my book, Statistical Programming with SAS/IML Software available as a free PDF document. The chapter is titled "Getting Started with the SAS/IML Matrix Programming Language," and it features More than 60 fully functional
Suppose that you compute the coefficients of a polynomial regression by using a certain set of polynomial effects and that I compute coefficients for a different set of polynomial effects. Can I use my coefficients to find your coefficients? The answer is yes, and this article explains how. Standard Polynomial
I was recently asked how to create a tridiagonal matrix in SAS/IML software. For example, how can you easily specify the following symmetric tridiagonal matrix without typing all of the zeros? proc iml; m = {1 6 0 0 0, 6 2 7 0 0, 0 7 3 8 0,
A previous post described a simple algorithm for generating Fibonacci numbers. It was noted that the ratio between adjacent terms in the Fibonacci sequence approaches the "Golden Ratio," 1.61803399.... This post explains why. In a discussion with my fellow blogger, David Smith, I made the comment "any two numbers (at
