The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs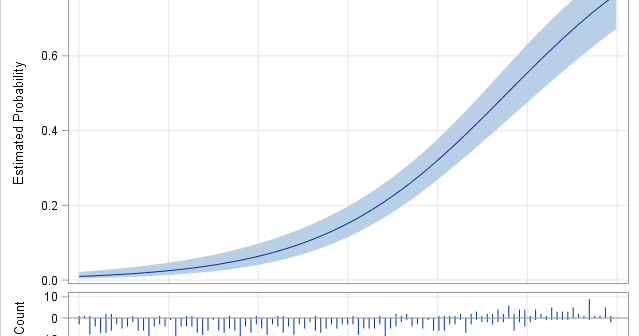
A previous article showed how to use a calibration plot to visualize the goodness-of-fit for a logistic regression model. It is common to overlay a scatter plot of the binary response on a predicted probability plot (below, left) and on a calibration plot (below, right): The SAS program that creates

The SAS language provides syntax that enables you to quickly specify a list of variables. SAS statements that accept variable lists include the KEEP and DROP statements, the ARRAY statement, and the OF operator for comma-separated arguments to some functions. You can also use variable lists on the VAR statements
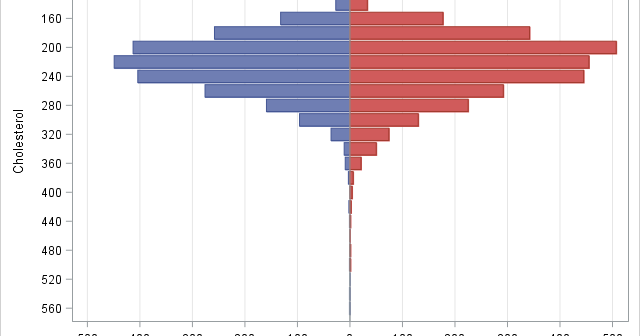
This article shows how to construct a butterfly plot in SAS. A butterfly plot (also called a butterfly chart) is a comparative bar chart or histogram that displays the distribution of a variable for two subpopulations. A butterfly plot for the cholesterol readings of 5,057 patients in a medical study
In a recent blog post, Chris Hemedinger used a scatter plot to show the result of 100 coin tosses. Chris arranged the 100 results in a 10 x 10 grid, where the first 10 results were shown on the first row, the second 10 were shown on the second row, and so
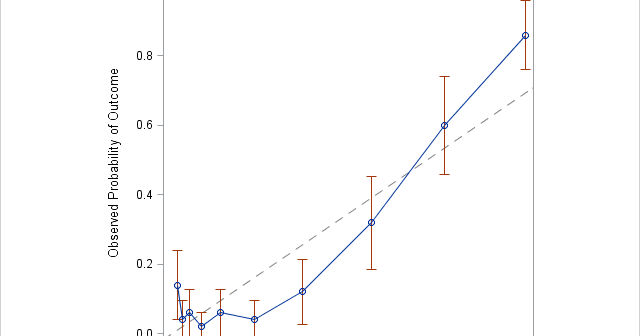
In my article about how to construct calibration plots for logistic regression models in SAS, I mentioned that there are several popular variations of the calibration plot. The previous article showed how to construct a loess-based calibration curve. Austin and Steyerberg (2013) recommend the loess-based curve on the basis of
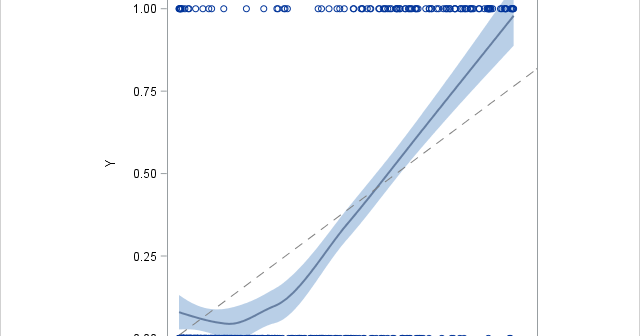
A logistic regression model is a way to predict the probability of a binary response based on values of explanatory variables. It is important to be able to assess the accuracy of a predictive model. This article shows how to construct a calibration plot in SAS. A calibration plot is
