Authors: Brandon Reese and Yan Xu
This post discusses the EURO Meets NeurIPS 2022 Vehicle Routing Competition. The competition brought together researchers from operations research (OR) and machine learning (ML). The purpose was to address vehicle routing problems with time windows (VRPTW) as well as a dynamic VRPTW.
Vehicle Routing Problems (VRPs) are a challenging yet essential part of supply chain logistics across many industries. Solving VRPs involves deciding how to best route a fleet of vehicles to make deliveries. One might seek optimal solutions to VRPs in terms of distance traveled, time taken, or fuel consumed. A sample VRP solution that uses three vehicles to satisfy the demands of 15 customers is depicted in Figure 1.
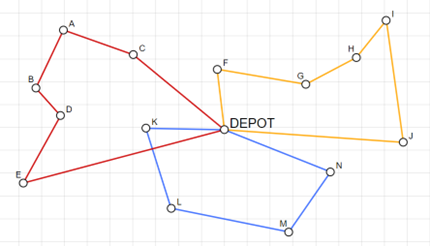
Many variants of VRP are classic problems in OR. Traditionally, the OR community has tackled VRP by formulating it as an optimization problem and then finding solutions by using exact or heuristic approaches. Recently, VRP has become a popular topic in the machine learning community because, despite its enormous business value in logistics and supply chain settings, traditional solvers have high computational costs.
EURO Meets NeurIPS 2022 Vehicle Routing Competition
As one of the most prestigious machine learning and AI conferences, NeurIPS 2022 attracted researchers and practitioners from all over the world. They exchanged the latest research ideas and progress in ML, deep learning, and AI. For 2022, NeurIPS had a hybrid format. The in-person portion took place in New Orleans, LA from November 28th to December 3rd. The virtual portion spanned December 5th to 9th. The competition was cosponsored by the EURO 2022 and NeurIPS 2022 conferences.
The EURO Meets NeurIPS 2022 Vehicle Routing Competition inspired researchers to find novel ways to improve upon state-of-the-art techniques in vehicle routing. The competition involved solving variants of capacitated VRPTW. In these variants, the solver must account for limitations on how much cargo each vehicle can carry. At the same time, it must satisfy constraints on the window of time at which each delivery can occur.
Defining the parameters
One variant, static VRPTW, is a well-studied problem. In this case, all the delivery requests are known from the start. The second variant, dynamic VRPTW, poses an additional challenge by introducing new delivery requests throughout the day. In this variant, the routing problem is presented incrementally, in one-hour blocks called epochs.
To produce a solution, it is necessary to predict whether delivery requests would be most efficiently served during the current epoch or a future epoch. In either variant, the number of available vehicles was not limited. The objective was to minimize the sum of distances traveled by all vehicles.
Competition results
The VRP competition was well received by both the OR and ML communities. According to the organizers, 150 teams registered, 50 teams submitted, and there were approximately 800 submissions from all teams. SAS’ Brandon Reese and Yan Xu formed a team, Miles To Go Before We Sleep (MTGBWS). The team also included SAS colleagues Steve Harenberg, Laci Ladanyi, and Rob Pratt. For the qualification phase, MTGBWS achieved 1st place for the static VRPTW variant, 13th place for the dynamic variant, and 7th place overall. For the final phase, MTGBWS finished 4th place for static VRPTW, 7th place for the dynamic variant, and 5th place overall.
Improved solutions to vehicle routing problems
The main improvements by MTGBWS came from two areas: new dispatch heuristics and software engineering. Applicable only to the dynamic VRPTW variant, dispatch heuristics are rules for deciding which delivery requests should be planned in the current epoch and which delivery requests should be deferred to a later one.
New dispatch heuristics
First, to apply a heuristic, the requested clients were labeled either “must-go” or “optional.” Must-go clients are those who must be dispatched in the current epoch because the time window associated with that client will expire during the current epoch. Optional clients are those whose time window would enable delivery during the current epoch or a future one.
Next, we calculated heuristic scores \(\alpha\) and D for each optional client for the nearest must-go client. See Figures 2 and 3. The minimum angle heuristic \(\alpha\) is helpful as it enables the selection of optional clients with small angular displacement relative to the depot and a must-go client. The minimum detour heuristic D is helpful as it enables the selection of optional clients with the smallest additional cost incurred when adding a stop at the optional client on the way from the depot to the must-go client.
Intuitively, in comparison to clients with high \(\alpha\) or D scores, clients with low \(\alpha\) or D scores would be less costly to insert into a route plan that already visits each must-go client.
By dispatching only the clients with the lowest score (either \(\alpha\) or D), we can effectively solve a static VRPTW subproblem considering only the must-go and selected optional set of clients. Planning to visit each client in that set should require a reasonably small detour when compared to the alternative scenario where we defer that client to a later epoch.
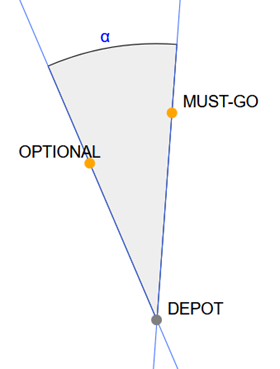
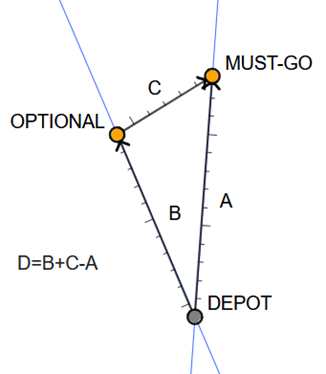
Both heuristics contributed to performance on the competition instances that was significantly improved compared to all the provided baseline dynamic VRPTW solvers.
Software engineering
To identify and address performance bottlenecks, we augmented the provided baseline implementation with automated benchmarks, profiling tools, and proper version control. With these software engineering fundamentals in place, we were able to ensure that only the code changes that produced the best overall performance improvements across the provided instances were submitted to the competition platform. Improving the execution speed of the solver led to a better performance on the static VRPTW variant than the baseline state-of-the-art solver. It was also better than that of most of the other competing teams. We found that the provided state-of-the-art baseline solver, HGS-VRPTW, was well-designed and well-tuned, so opportunities for improvement were slim.
The team experimented with many novel enhancements that were combined to produce better solutions on both VRPTW variants. These enhancements included rewriting, refactoring, and optimizing the source code in ways that guaranteed small but measurable improvements. For example, swapping out data structures for more efficient ones enabled us to refactor away costly loop computations. This enabled us to perform simpler, faster lookup computations.
A main differentiator was the achievement of exact and repeatable results. Early in the competition, we noticed that repeated submissions often resulted in significantly different solution costs. Until we addressed the nondeterminism in the solver, our benchmarking efforts would be less effective. The use of debugging, static analysis, and profiling tools enabled us to first address the nondeterminism so that we could reliably measure our algorithm improvements. By focusing on performance improvements that produced the exact same sequence of results but in less time, we were able to fully trust our benchmarking experiments. This ensured that each new version would perform equally or better than the previous one on the hidden leaderboard.
Conclusion
In summary, the EURO Meets NeurIPS 2022 Vehicle Routing Competition provided an exciting opportunity for researchers and practitioners to try new ideas in the fields of OR and ML to improve upon the current state-of-the-art in VRP solver technology. By bringing these two research communities together, creative new approaches to solving a business-critical problem were developed and shared. The team applied the operations research and software engineering tools and disciplines that have ensured the robust, fast performance of SAS software. The contributions are just one of the many ways that SAS is looking outwards and contributing to state-of-the-art technology.








1 Comment
Interesting problem, and a fascinating solution approach!