指数関数的成長の倍加時間を推計する

この記事はSAS Institute Japanが翻訳および編集したもので、もともとはRick Wicklinによって執筆されました。元記事はこちらです（英語）。

2020年における新型コロナウイルスの世界的流行のようなエピデミック状況下では、各国の感染確認者の累計数を示すグラフがメディアによって頻繁に示されます。多くの場合、これらのグラフは縦軸に対数スケール（対数目盛）を使います。このタイプのグラフにおける直線は、新たなケースが指数関数的ペースで急増していることを示します。直線の勾配はケースがどれほど急速に倍加するかの程度を示し、急勾配の直線ほど倍加時間が短いことを示します。ここでの「倍加時間」とは、「関連状況が何も変わらないと仮定した場合に、累計の感染確認者数が倍増するまでに要する時間の長さ」のことです。
本稿では、直近のデータを用いて倍加時間を推計する一つの方法を紹介します。この手法は、線形回帰を用いて曲線の勾配（m）を推計し、その後、倍加時間を log(2) / m として推計します。
本稿で使用しているデータは、2020年3月3日～3月27日の間の、4つの国（イタリア、米国、カナダ、韓国）における新型コロナウイルス感染症（以下、COVID-19）の感染確認者の累計数です。読者の皆さんは、本稿で使用しているデータとSASプログラムをダウンロードすることができます。

累計感染者数の対数スケール・ビジュアライゼーション

このデータセットには4つの変数が含まれています。

変数Region：国を示します。
変数Day： 2020年3月3日からの経過日数を示します。
変数Cumul： COVID-19の感染確認者の累計数を示します。
変数Log10Cumul：感染確認累計数の「10を底とする対数」（＝常用対数）を示します。SASでは、LOG10関数を用いて常用対数を計算することができます。

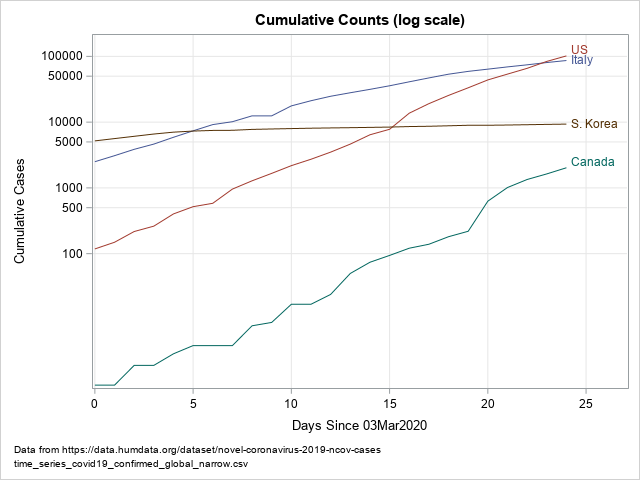
これらのデータをビジュアル化する目的には、PROC SGPLOTを使用できます。下図のグラフは感染確認者の総数をプロットしていますが、総数の縦軸に常用対数を指定するために「type=LOG」と「logbase=10」というオプションを使用しています。

title "Cumulative Counts (log scale)";
proc sgplot data=Virus;
  where Cumul > 0;
  series x=Day y=Cumul / group=Region curvelabel;
  xaxis grid;
  yaxis type=LOG logbase=10 grid
        values=(100 500 1000 5000 10000 50000 100000) ValuesHint;
run;

このようなグラフは、1つの軸のみが対数スケールで表示されることから、「片対数グラフ」と呼ばれることもあります。片対数グラフ上の直線は指数関数的な成長を示します。しかしながら、全ての指数関数的成長が等価ということではありません。直線の勾配は成長がどれほど急速に進行しているかを示しており、倍加時間はその成長［の速さ］を測定する一つの手段です。急勾配の直線は「基底にある数量（この例の場合は感染確認者数）が短期間で倍増するだろう」ということを示します。平坦な直線は「基底にある数量が急速には成長せず、倍増には長い期間がかかるだろう」ということを示します。本稿のデータの場合、このビジュアライゼーションは以下の事実を明らかにしています。

米国およびカナダの曲線は急勾配である。
韓国の曲線は平坦の度合いが非常に高い。これは「同国では感染確認者数の増加ペースが非常に遅い」ということを示している。
イタリアの曲線の勾配は、0～6日目の区間では米国に似ているが、その後は平坦に近づき始める。24日目の時点で米国とイタリアの感染確認者数は同数だが、イタリアの曲線の勾配は米国のそれよりも緩やかだった。これは、「（24日目の時点では）米国における感染者数の推定倍加時間は、イタリアのそれよりも短期間である」と解釈されます。

それぞれの曲線の終端における勾配の推計

一部の研究者は、曲線上の “全て” の値に対して線形回帰を当てはめることで平均勾配を推計します。これは通常は得策ではありません。なぜなら、各種の介入要因（“ステイホーム（外出自粛）” 要請など）が時の経過とともに曲線の勾配を変動させるからです。イタリアと韓国の曲線には、こうした変動が明らかに見てとれます。
直近のデータ値のみを用いて回帰線を当てはめれば、今現在の成長レートをより高精度に推計することができます。私が提唱するのは、例えば直前の5～7日間など、過去数日間のデータを使用することです。直近の5つのオブザベーション（観測値）に基づいて各グラフ線の勾配を推計する目的には、SASのREGプロシジャを使用できます。

%let MaxDay = 24;
proc reg data=Virus outest=Est noprint;
  where Day >= %eval(&MaxDay-4);           *previous 5 days: Day 20, 21, 22, 23, and 24;
  by Region notsorted;
  model log10Cumul = Day;
quit;

出力データセットであるEstには、直近データにベストフィットするグラフ線の勾配（および切片）の推計値が格納されます。これらの推計値ついては後続セクションで取り上げます。

倍加時間の推計

これらの推定された勾配を使えば、それぞれの曲線の倍加時間を推計することができます。もし数量Yが、ある時点（t₀）の Y₀ から、少し後の時点（t₀ + Δt）の 2*Y₀ へと増えるとすると、値 Δt が倍加時間となります。次の段落では、t₀ における倍加時間が log(2) / m（ここで m は、t₀ における勾配の推計値）であることを示します。
考え方としては、「t₀ における接線を用いて倍加時間を推計する」ということです。ここでは、log(Y) = m*t + b を「この片対数グラフの t₀ における接線の方程式」とします。Y が Y₀ から 2*Y₀ に増加すると、対数は log(Y₀) から log(2*Y₀) = log(2) + log(Y₀) へと増加します。勾配は “Rise over Run”（上方向の変化量 ÷ 右方向の変化量）であることから、接線が2倍の値に到達するのは、
m = [(log(2) + log(Y₀)) - log(Y₀)] / Δt = log(2) / Δt
の時点です。
ここで Δt を求めると、
Δt = log(2) / m
（ここで m は、t₀ における片対数曲線に対する回帰線の勾配）
となります。この式が倍加時間を推計するということは、「倍加時間は Y の値には依存せず、t₀ における勾配のみに依存する」ということになります

勾配から倍加時間を推計する

下記のSAS DATAステップは、それぞれの曲線の終端（24日目）における勾配を用いて倍加時間を推計します。

data DoublingTime;
set Est(rename=(Day=Slope));
label Slope = "Slope of Line" DoublingTime = "Doubling Time";
DoublingTime = log10(2) / Slope;
keep Region Intercept Slope DoublingTime;
run;
 
proc print data=DoublingTime label noobs;
  format Slope DoublingTime 6.3;
  var Region Slope DoublingTime;
run;

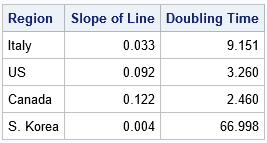
パンデミックに関しては、短い倍加時間は悪い兆候であり、長い倍加時間は良い兆候です。2020年3月27日のデータに基づくこの表には、イタリアにおける推計倍加時間が約9日間と示されています。対照的に、米国における倍加時間の推計値は約3.3日間、カナダにおける推計値は約2.5日間です。韓国の推計値は67日間ですが、これほど長い期間に関しては、恐らく「関連状況が何も変化しない」という仮定が妥当性を失います。

倍加時間をビジュアル化する

それぞれの曲線の終端に矢印を追加すれば、倍加時間を視覚的に示すことができます。

矢印の起点は直近データ上に置きます。
矢印の方向は、その曲線に対して推計された勾配によって決まります。
矢印の水平方向の増分が倍加時間です。
矢印の垂直方向の増分は、現在の累積数と等しくなります（＝矢印の終点の累積数は現在の累積数の2倍になります）。

矢印を加えたビジュアライゼーションを下図に示します（ここでは韓国を除外してあります）。

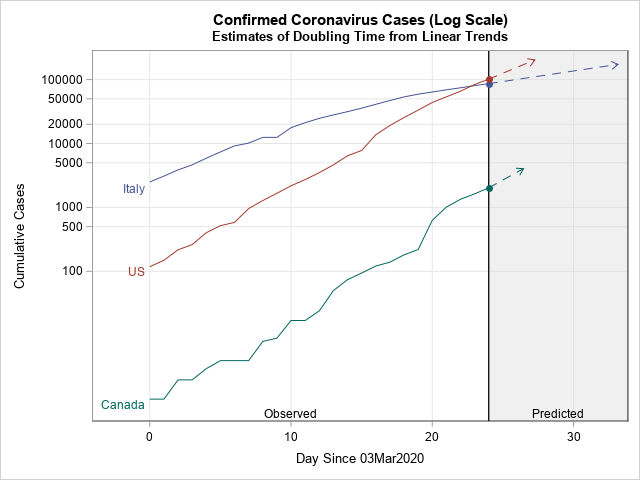
このグラフを見ると、米国とカナダの累積数がどれほど短期間で2倍になると予測されているかが分かります。それぞれの矢印の先端は、感染確認者数が2倍になると予想される時点を示しています。米国とカナダでは、ほんの数日後です。イタリアの矢印は、感染確認者数の倍増までに比較的長い期間がかかることを示しています。繰り返しますが、これらの計算は「感染確認者数が、24日目時点の推計増大レートで増え続ける」と仮定しています。イタリアの曲線は平坦化しつつあるように見えるため、このイタリアに関する推計結果は悲観的すぎるでしょう（と言える状況になることを祈念します）。

まとめ

要点は、（対数スケールグラフ上の）累積曲線の勾配を使用すれば、基底にある数量の倍加時間を推計することができる、ということです。直近のオブザベーションにおける勾配を求めるには、直近のデータに線形回帰線を当てはめます。倍加時間は、log(2)/m（m は片対数グラフにおける累積曲線の勾配の推計値）によって求めることができます。倍加時間をグラフ上でビジュアル化したい場合は、それぞれの曲線の終端に矢印を追加することができます。

Blogs