At the time this blog entry was written, there still appears to be little to no signs of locating the missing Malaysian flight MH370. The area of search, although already narrowed down from the size of the United States at one point to the size of Poland, is still vast and presents great challenges to all participating nations. Everything we’ve seen in the news so far have been leads that turn out to be nothing but dead ends.
There are a great many uncertainties surrounding the disappearance of flight MH370, making a search and rescue operation all but seem like finding a needle in an ocean-sized haystack. There is, however, an already established statistical framework based on Bayesian inference that has had great success in locating, amongst other things, a Hydrogen bomb lost over the Mediterranean sea1, a sunken nuclear submarine from the US Navy (USS Scorpion)1, and the wreckage of Air France Flight 447 just several years ago.
The U.S. Coast Guard’s SAROPS (Search and Rescue Optimal Planning System) is based on the same Bayesian search framework that’s refined to accommodate ocean drift and crosswinds. As there is currently no evidence that the Malaysian government or Malaysian airlines is employing a Bayesian optimal search method, it is worthwhile to point out why a Bayesian search strategy should at least be considered for a situation such as the missing MH370 case.
Unknown variables
First of all, there are still many unknowns regarding the missing MH370. Unknown variables are typically modeled probabilistically in the statistical world. Most of us are familiar with the frequency definition of probability. If I handed you an old beat-up coin and asked you to tell me what the probability of heads is if the coin is flipped, your best bet is to flipped the coin say 5000 times and record the number of times it came up heads. Then you would divide the number of heads by 5000 and get a pretty good estimate of the probability in question. This is the frequency interpretation of probability: the probability of an event is the relative frequency of the event happening in an infinite population of repeatable trials.
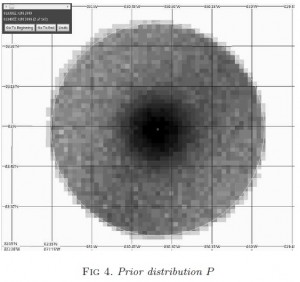
In the real world, however, we are often faced with rare and unique events, events that are non-repeatable. Hopefully, we wouldn’t have to study 5000 plane crashes to get a good estimate of a plane accident happening. In reality, there have only been 80 recorded missing planes since 1948. This calls for a different interpretation of probability, a subjective one that reflects an expert’s degree of belief. The subjective nature of the uncertainties of a rare event such as the loss of flight MH370 places us squarely in the domain of Bayesian inference. In the case of Air France 447, the prior distribution (initial belief about the crash location) of the search area was taken to be a mixture of three probability distributions, each representing a different scenario. The mixture weights were then decided based on consultations with experts at the BEA.
All information is useful
A big advantage of employing a Bayesian search method is that a Bayesian framework provides a systematic way to incorporate all available information via Bayes’ rule. This is invaluable in a large and complex search operation where new information will constantly emerge and the situation could change at a moment’s notice, requiring the search strategy to be constantly updated. The important thing to note here is that any information is considered useful. One area turning up empty will lower the probability of the wreckage in that area after a Bayesian update, but at the same time, it will increase the probability of the wreckage in other areas yet unsearched.
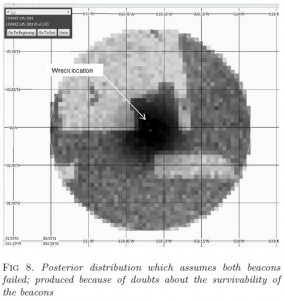
Air France 447 went missing in June 2009, when BEA commissioned scientific consulting firm Metron Scientific Solutions to come up with a probability map of the search area in 2011, two years of search efforts had turned up nothing. In their model, the Metron team took into account all four unsuccessful previous searches when updating their prior distribution of the crash location. Based on their recommendation of resuming the new round of search efforts around the region with the highest posterior probability, the wreck was located only one week into the search2.
While there are many intricate steps involved in deploying a Bayesian search strategy, particularly in coming up with the prior distribution and quantifying the likelihood of the different accident scenarios, the core math involved is surprisingly straightforward. For illustration purposes, assume that the search area is divided up into N grids, labelled x1 through xN. Let the prior probability of the wreck being in grid xk be denoted by p(xk+), for k=1,…,N. Now let the probability of successful detection in grid xk given the wreck is in grid xk be denoted p(Sk+|xk+). If the search in grid xk turns up empty, then the posterior probability of the wreck being in grid xk given the fact that the search in grid xk is unsuccessful is:
Meanwhile the posterior probability of the wreck being in any other grid xm is also updated by the information that the search in grid xk turned up unsuccessful:
Note that p(xk+|Sk-) < p(xk+), and p(xm+|Sk-) > p(xm+).
A Bayesian search strategy would start from the grids with the highest prior probability mass, if nothing is found in those grids then update the posterior probability of all grids via Bayes theorem and start all over treating the new posterior probabilities as current prior probabilities. This could be a lengthy process, but as long as the wreck is located within the prior region, it would eventually be located.
An unprecedented search area
When AF447 crashed, BEA was able to quickly establish that the plane would have to lie within a 40 nautical mile radius circle from the plane’s last known location. This is roughly 6600 square miles of initial search area, compare to MH370’s current Poland-sized search area of more than 100,000 square miles. Considering it took two years, and five rounds of search efforts to finally locate AF447, the difficulty involved in finding MH370 is unprecedented in the history of modern aviation. While a Bayesian search method might not locate the remains of MH370 any time soon, its flexibility and systematic nature, not to mention its past successes, makes it a powerful tool to seriously consider for the current search efforts.
For interested readers, here is the paper that documented the Metron teams’ efforts in using Bayesian inference to develop the probability map of AF447’s location.
References:
1. S. B. McGrayne. “The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy”, Yale University Press, 2011.
2. L. D. Stone, C. M. Keller, T. M. Kratzke and J. P. Strumpfer. “Search for the Wreckage of Air France Flight AF 447”, submitted to Statistical Science, 2013.
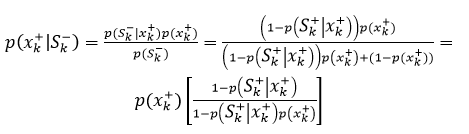







3 Comments
Bayes Rulez !
I think we cannot say bayesian approach accelerated the search process in AF447. The previous two years' search provide the prior information for bayesian approach. Otherwise, they wouldn't find the wreckage in one week after the consulting firm stepped in.
However, bayesian search is for sure better than random search.
Liwen, thanks for the comment. Without a systematic way to combine the information from the previous two years of search, it might've taken much longer than 1 week to locate AF447. Had they started from day one with a Bayesian strategy, it's possible to locate the wreck sooner. Notice how the high density area surrounding the last known location didn't change that much from prior to posterior, which means they would've focused on this area much sooner had authorities been pointed to this region after say the first two rounds of Bayesian updates.