みなさま、こんにちは。
さて突然ですが、フーリエ変換ってご存知ですか?
おそらく物理学や経済学で波形データを分析したことのある方には馴染みがあるでしょうが、フーリエ変換は波形データを扱う手法です。
フーリエ変換では周期的な波形を、sin波やcos波の重ね合わせで説明しようというものです。
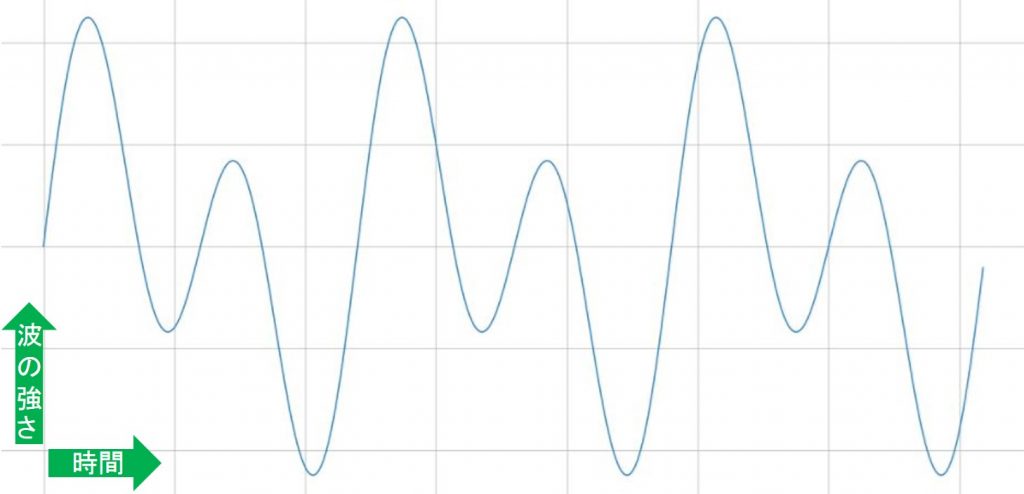
たとえば以下のような波形データは、どの時間にどのくらいの強さの波が流れているかを表現しています。
これをフーリエ変換することで、周波数と振幅で表すことができるようになります。
↓ フーリエ変換! ↓
従来のSAS製品では波形データでフーリエ変換をする機能を提供していなかったのですが、SAS ViyaのSAS Forcastingという製品を使うことで、フーリエ変換を実施することができるようになりました。
SAS Viyaでできるのは短時間フーリエ変換(Short time Fourier transform)です。
今回はSAS Viyaでフーリエ変換を実施してみたいと思います。プログラミング言語はPythonを使用します。
まずは前準備として、必要なライブラリをインポートし、CAS sessionを作成します。
CAS sessionはSAS Viyaでデータ分析を行うCASというエンジンへ認証し、接続するものです。
# CAS sessionの用意 import swat host = "localhost" port = 5570 user = "user" password = "p@ssw0rd" mysession = swat.CAS(host, port, user, password) # datastep, timeFrequency actionsetをロード actionsets = ["datastep", "timeFrequency"] for act in actionsets: mysession.loadactionset(act) |
これでSAS Viyaを使う準備ができました。
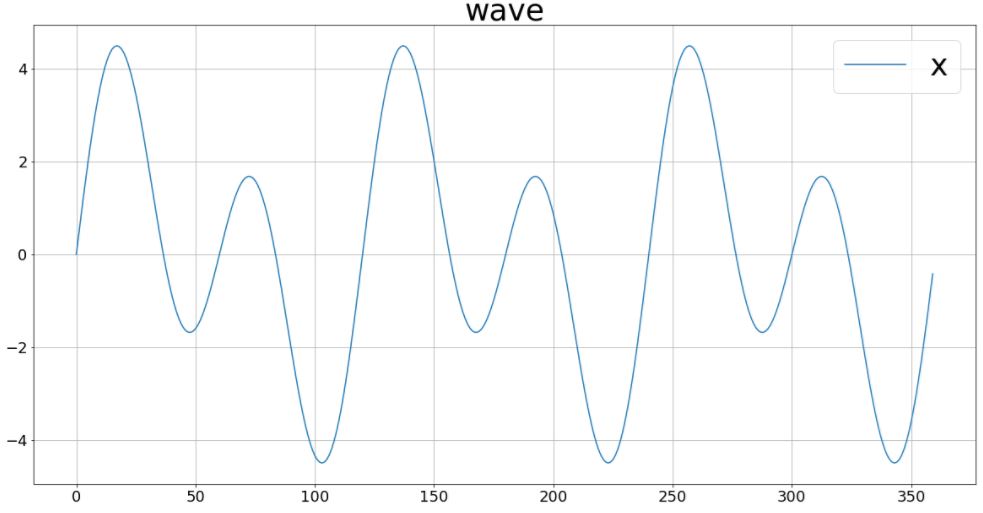
続いてフーリエ変換を行うための波形データを用意します。今回はデータステップで波形データを生成し、グラフ化します。
# datastep actionsetを使うことで、Python上でSAS Datastepを書くことができます。 # ここでは2つのサイン波を合成したデータセットを用意します。 chirp = mysession.dataStep.runCode( code="data casuser.chirp; \ keep time x; \ do time = 0 to 719; \ x = 2 * sin(1 * constant('pi') * time / 60) + \ 3 * sin(2 * constant('pi') * time / 60); \ output; \ end; \ run;", nThreads=1, single="YES") # データセットをグラフ化します。 import matplotlib.pyplot as plt plt.figure(figsize=(20,10)) plt.plot(mysession.CASTable("chirp").head(n=360)["x"]) plt.grid(True) plt.legend(loc="best", fontsize=36) plt.title("wave", fontsize=36) plt.tick_params(labelsize=18) plt.show() |
余談ですが、SAS ViyaではPythonからSASデータステップを実行することができるようになっています。dataStep.runCodeというActionでSASデータステップをそのまま実行できるので、PythonもSASデータステップも使いたいという方にはとても親切な作りになっています。
次は窓関数を用意します。フーリエ変換では波形データを、区間を区切って取り込みます。波形データを取り込んだ区間の繰り返しと想定して変換するのですが、取り込み区間が実際の波形データの周期と同期するとは限りません。むしろずれることの方が多いと思います。そこで窓関数を当てることで誤差を軽減します。
窓関数にはいくつか種類があるのですが、今回はハニング窓を用意します。
# ハニングで長さ128の窓関数を生成します。 window = mysession.timeFrequency.window(winId="HANNING", winLen=128) # サイン波と窓関数を重ねてグラフ化します。 plt.figure(figsize=(20,10)) plt.plot(mysession.CASTable("chirp").head(n=180)["x"]) plt.plot(window["win"]) plt.grid(True) plt.legend(loc="best", fontsize=36) plt.title("wave with window", fontsize=36) plt.tick_params(labelsize=18) plt.show() |
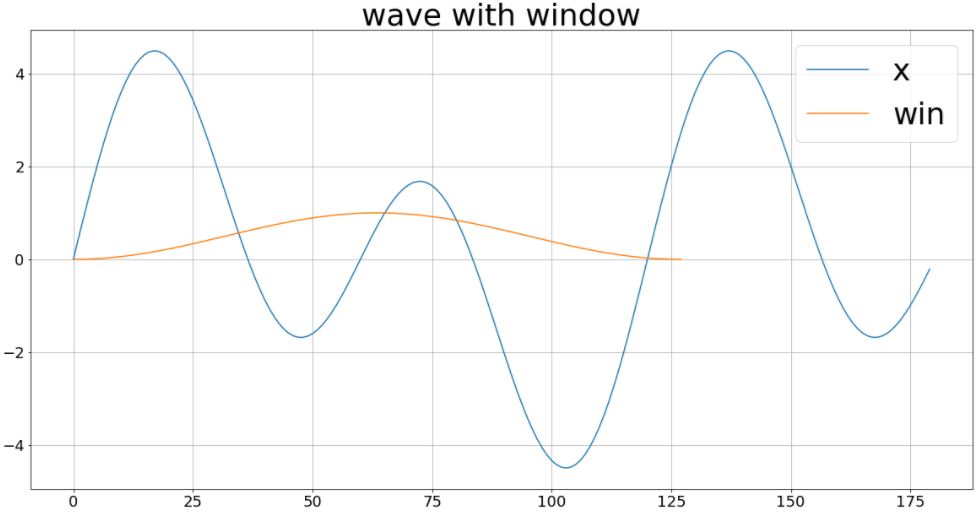
フーリエ変換の際には、ここで作ったハニング窓を波形データの取り込み区間上でスライドながら当てて、区切りをきれいに繋げることができます。
それでは最後にフーリエ変換して、結果をグラフにしてみましょう。SAS Viyaのフーリエ変換ではtimeFrequency.stftというActionを使います。stftはshort time Fourier transform(短時間フーリエ変換)の略です。
# 短時間フーリエ変換(sft)を実行します。 # 入力データの長さ(signalLength)、波長(fftLen)を256、オーバーラップ(nOverlap)を64(窓関数の半分)を入力します。 stft = mysession.timeFrequency.stft( table={'name':'chirp'}, signalLength=len(mysession.CASTable("chirp")), window=window['win'].value.tolist(), nOverlap=64, fftLen=256, casOut='stftOut' ) |
結果としてこのようなデータが出力されます。表のcoeff_reが実数型、coeff_imがオイラーの公式で展開された複素数型です。
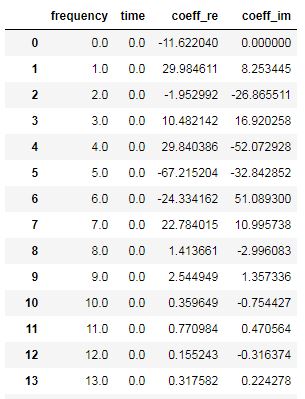
実数型をグラフ化してみます。
# 実数型。 plt.figure(figsize=(20,10)) plt.plot(mysession.CASTable("stftOut").head(n=360)["coeff_re"]) plt.ylabel("coeff_re", fontsize=36) plt.grid(True) plt.legend(loc="best", fontsize=36) plt.title("coeff_re", fontsize=36) plt.tick_params(labelsize=18) plt.show() |
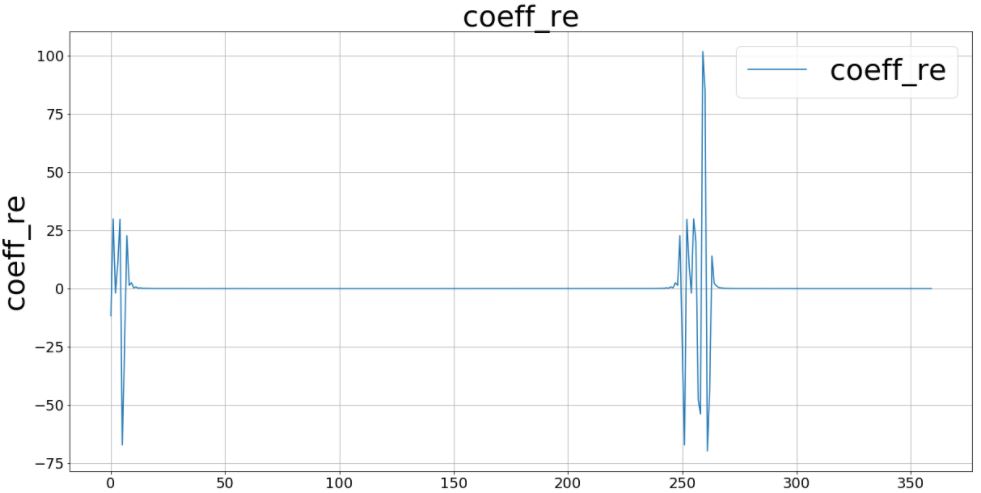
特定の周波数で振幅が発生していることが見て取れます。