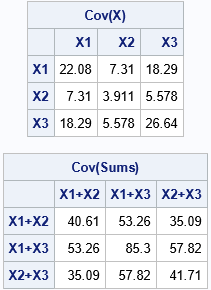
A lot of programmers have been impressed by the ability of ChatGPT, GPT-4, and Bing Chat to write computer programs. Recently, I wrote an article that discusses an elementary programming assignment, called FizzBuzz, which is sometimes used as part of a hiring process to assess a candidate's basic knowledge of