Nikolaos Kourentzes is Associate Professor at Lancaster University, and a member of the Lancaster Centre for Forecasting. In addition to having a great head of hair for a forecasting professor, Nikos has a great head for explaining fundamental forecasting concepts.

In his recent blog post on How to choose a forecast for your time series, Nikos discusses the familiar validation (or "hold out") sample method, and the less familiar approach of using information criteria (IC). Using an IC helps you avoid the common problem of "overfitting" a model to the history. We can see what this means by a quick review of the time series forecasting problem.

The Time Series Forecasting Problem

A time series is a sequence of data points taken across equally spaced intervals. In business forecasting, we usually deal with things like weekly unit sales, or monthly revenue. Given the historical time series data, the forecaster's job is to predict the values for future data points. For example, you may have three years of weekly sales history for product XYZ, and need to forecast the next 52 weeks of sales for use in production, inventory, and revenue planning.

There is much discussion on the proper way to select a forecasting model. It may seem obvious to just choose a model that best fits the historical data. But is that such a smart thing?

Unfortunately, having a great fit to history is no guarantee that a model will be any good at forecasting the future. Let's look at a simple example to illustrate the point:

Suppose you have four weeks of sales: 5, 6, 4, and 7 units. What model should you choose to forecast the next several weeks? A simple way to start with with an average of the 4 historical data points:

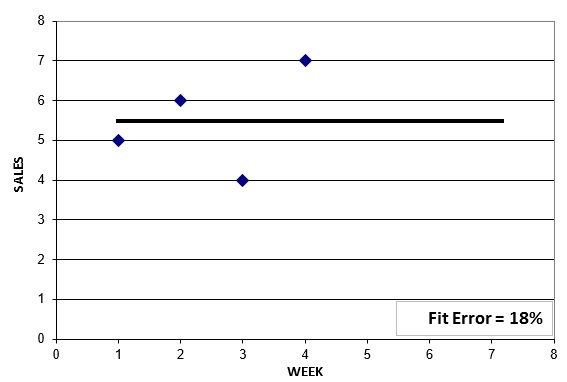
We see this model forecasts 5.5 units per week into the future, and there is an 18% error in the fit to history. Can we do better? Let's try a linear regression to capture any trend in the data:

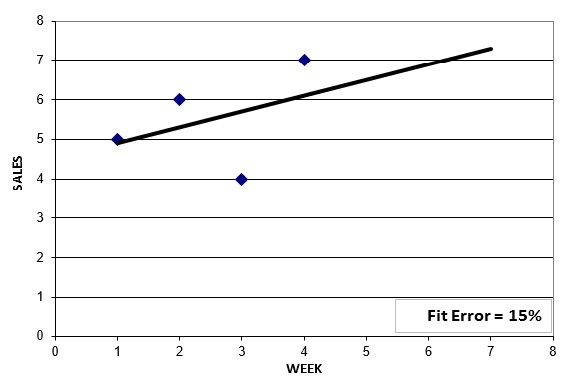
This model forecasts increasing sales, and the historical fit error has been reduced to 15%. But can we do better? Let's now try a quadratic model:

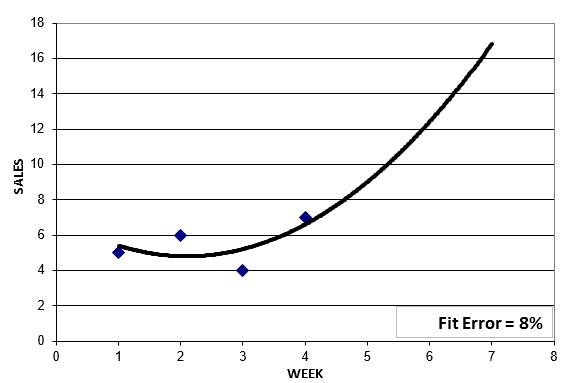
The quadratic model cuts the historical fit error in half to 8%, and it is also showing a big increase in future sales. But we can do even better with a cubic model:

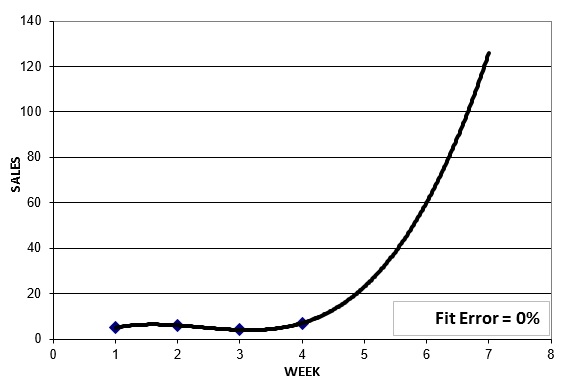
It is always possible to find a model that fits your time series history perfectly. We have done so here with a cubic model. But even though the historical fit is perfect, is this an appropriate model for forecasting the future? It doesn't appear to be. This is a case of "overfitting" the model to the history.

In this example, only the first two models, the ones with the worst fit to history, appear to be reasonable choices for forecasting the near term future. While fit to history is a relevant consideration when selecting a forecasting a model, it should not be the sole consideration.

In the next post we'll look at Nikos' discussion of validation (hold out) samples, and how use of information criteria can help you avoid overfitting.