The new book Business Forecasting: Practical Problems and Solutions contains a large section of recent articles on forecasting performance evaluation and reporting. Among the contributing authors is Rob Hyndman, Professor of Statistics at Monash University in Australia.

To anyone needing an introduction, Hyndman's credentials include:

Editor-in-chief of International Journal of Forecasting

Board of Directors of the International Institute of Forecasters

Co-author (with Makridakis and Wheelwright) of the classic textbook Forecasting: Methods and Applications (3rd edition)

• Author of the influential blog Hyndsight.

Drawing from his online textbook Forecasting: Principles and Practice (coauthored with George Athanasopoulos), Hyndman explains the use of Training and Test sets for measuring forecast accuracy.

Rob Hyndman on Measuring Forecast Accuracy

A common "worst practice" is to select forecasting models based solely on their fit to the history that was used to construct them. As Hyndman points out, "A model that fits the data well does not necessarily forecast well."

Unscrupulous consultants or forecasting software vendors can wow impressionable customers with models that closely (or even perfectly) fit their history. Yet fit to history provides little indication of how well the model will actually forecast the future.

Hyndman's article discusses scale-dependent errors (e.g., MAE and RMSE), percentage errors (MAPE), and scaled errors (MASE), and the situations in which each are appropriate. Note that scaled errors are a relatively new type of forecasting performance metric, first proposed by Hyndman and Koehler in 2006. [Find more details in their article: Another look at measures of forecast accuracy. International Journal of Forecasting 22(4), 679-688.]

To avoid the worst practice mentioned above, Hyndman suggests dividing history into "training data" (used to estimate the model) and "test data" (used to evaluate forecasts generated by the model). The test data is often referred to as a "hold out sample," and this is a well-recognized approach.

 

 

When there is sufficient history, about 20% of the observations (the most recent) should be "held out" to serve as test data. The test data should be at least as large as the maximum forecast horizon required. So hold out 12 months (or 52 weeks) if you have to forecast one year out.

Unfortunately, we often don't have enough historical data for the recommended amount of test data. So for shorter time series, Hyndman illustrates the method of time series cross-validation, in which a series of training and test sets are used.

Time Series Cross-Validation

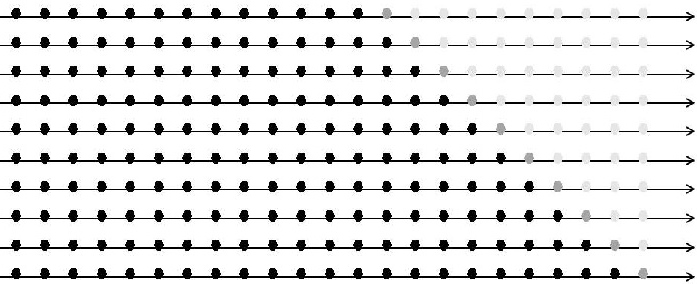
This approach uses many different training sets, each one containing one more observation then the previous one. Suppose you want to evaluate the one-step ahead forecasts.

As we see in this diagram, each training set (black dots) contains one more observation than the previous one, and each test set (gray dots) contains the next observation. The light gray dots are ignored. Per Hyndman:

Suppose k observations are required to produce a reliable forecast. Then the process works as follows.

1. Select the observation at time k+i for the test set, and use the observations at times 1, 2,…, k+i − 1 to estimate the forecasting model. Compute the error on the forecast for time k+i.
2. Repeat the above step for i = 1, 2,…, T − k where T is the total number of observations.
3. Compute the forecast accuracy measures based on the errors obtained.

So if you had T=48 months of historical data and used the first 36 as your test set, then you would have 12 one-step ahead forecasts over which to compute your model's accuracy.

In the next post, we'll look at the more general (and more common) situation where you are interested in models that produce good h-step-ahead forecasts (for example, for 3 months ahead).