Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
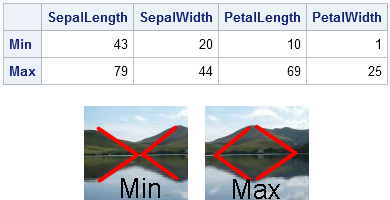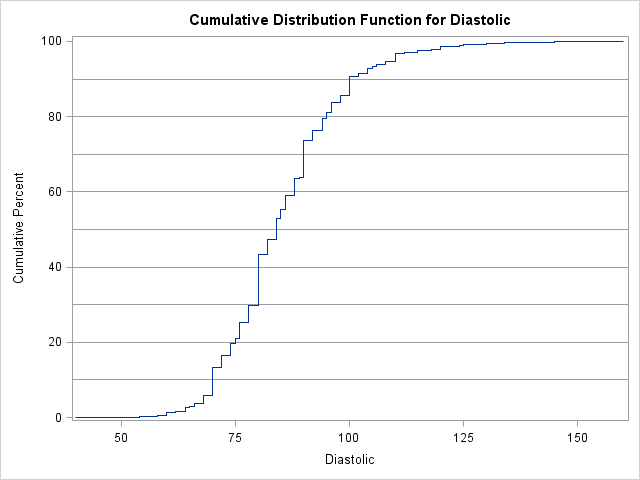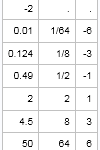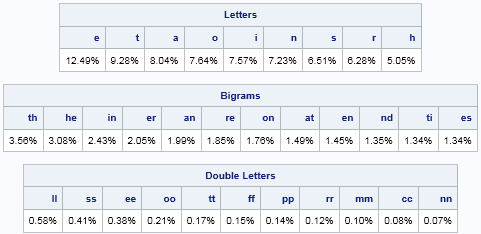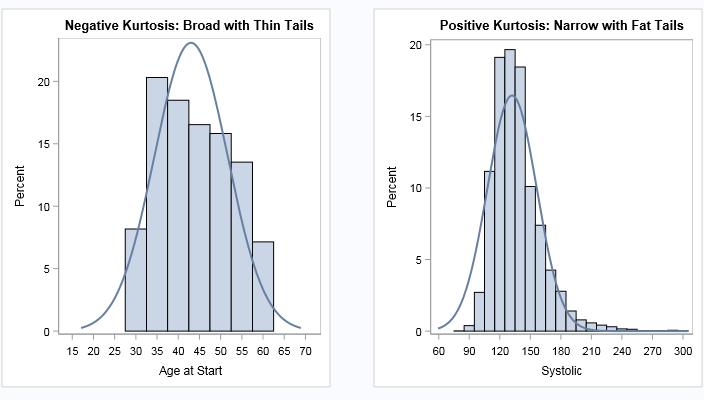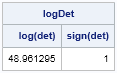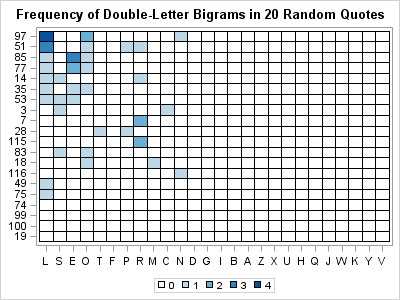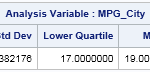
Pascal's triangle is the name given to the triangular array of binomial coefficients. The nth row is the set of coefficients in the expansion of the binomial expression (1 + x)n. Complicated stuff, right? Well, yes and no. Pascal's triangle is known to many school children who have never heard of polynomials
A common question on SAS discussion forums is how to compute the minimum and maximum values across several variables. It is easy to compute statistics across rows by using the DATA step. This article shows how to compute the minimum and maximum values for each observation (across variables) and, for
I've written about how to generate a sample from a multivariate normal (MVN) distribution in SAS by using the RANDNORMAL function in SAS/IML software. Last week a SAS/IML programmer showed me a program that simulated MVN data and computed the resulting covariance matrix for each simulated sample. The purpose of
SAS software contains a lot of features, and each release adds more.To make sure that you do not miss new features that appear in the SAS/IML language, the word cloud on the right sidebar of my blog contains numbers that relate to SAS or SAS/IML releases. For example, you can
My colleagues at the SAS & R blog recently posted an example of how to program a permutation test in SAS and R. Their SAS implementation used Base SAS and was "relatively cumbersome" (their words) when compared with the R code. In today's post I implement the permutation test in
I sometimes wonder whether some functions and options in SAS software ever get used. Last week I was reviewing new features that were added to SAS/IML 13.1. One of the new functions is the CV function, which computes the sample coefficient of variation for data. Maybe it is just me,
Have you ever noticed that some SAS/IML programmers use the CALL statement to call a subroutine, whereas others use the RUN statement? Have you ever wondered why the SAS/IML language has two statements that do the same thing? It turns out that the CALL statement and the RUN statement do
When I studied high school geometry, I noticed that many homework problems involved right triangles whose side lengths were integers. The canonical example is the 3-4-5 right triangle, which has legs of length 3 and 4 and a hypotenuse of length 5. The triple (3, 4, 5) is called a
I was recently asked about how to use the SAS/IML language to efficiently add a constant to every element of a matrix diagonal. Mathematically, the task is to form the matrix sum A + kI, where A is an n x n matrix, k is a scalar value, and I is the
My colleague Robert Allison has a knack for finding fascinating data. Last week he did it again by locating data about how blood types and Rh factors vary among countries. He produced a series of eight world maps, each showing the prevalence of a blood type (A+, A-, B+, B-,
In my article about how to create a quantile plot, I chose not to discuss a theoretical issue that occasionally occurs. The issue is that for discrete data (which includes rounded values), it might be impossible to use quantile values to split the data into k groups where each group
It has been three months since the introduction of the SAS/IML File Exchange, so I thought I'd give a short update on recent submissions and activity. (Note: The File Exchange was merged into the SAS Community Library in 2022.) Users have submitted eight new articles. The application areas include experimental
The other day I was doing some computations that caused me to wonder, "What is the smallest power of 2 that is greater than a given number?" The mathematics is straightforward. Given a number n, find the least value of k such that 2k ≥ n or, equivalently, k ≥
Many people enjoy solving word games such as the daily Cryptoquote puzzle, which uses a simple substitution cipher to disguise a witty or wise quote by a famous person. A common way to attack the puzzle is frequency analysis. In frequency analysis you identify letters and pairs of letters (bigrams)
One of my presentations at SAS Global Forum 2014 was about the new heat map functions in SAS/IML 13.1. Over the summer I created a short video of my presentation, which gives an overview of visualizing matrices with heat maps, and describes how to choose colors for heat maps: If
What is kurtosis? What does negative or positive kurtosis mean, and why should you care? How do you compute kurtosis in SAS software? It is not clear from the definition of kurtosis what (if anything) kurtosis tells us about the shape of a distribution, or why kurtosis is relevant to
A few years ago I wrote an article that shows how to compute the log-determinant of a covariance matrix in SAS. This computation is often required to evaluate a log-likelihood function. My algorithm used the ROOT function in SAS/IML to compute a Cholesky decomposition of the covariance matrix. The Cholesky
My previous blog post describes how to implement Conway's Game of Life by using the dynamically linked graphics in SAS/IML Studio. But the Game of Life is not the only kind of cellular automata. This article describes a system of cellular automata that is known as Wolfram's Rule 30. In
A colleague jokingly teases me whenever I write a blog that demonstrates how to write fun and exciting programs by using SAS software. "Why do you get to have all the fun?" he mock-chides. Today I'm ready to face his ribbing, because this article is about Conway's Game of Life
The tail of a probability distribution is an important notion in probability and statistics, but did you know that there is not a rigorous definition for the "tail"? The term is primarily used intuitively to mean the part of a distribution that is far from the distribution's peak or center.
It usually takes more than three weeks to prepare a good impromptu speech. --Mark Twain In the popular Cryptoquote puzzle, you are presented with an enciphered version of a quote by a famous person. One of the appeals of the puzzle for me is reading the deciphered quote, such
SAS/IML 13.1 includes a handy function for programmers who write a lot of modules. The PARENTNAME function obtains the name of the symbol that was passed in as a parameter to a user-defined module. How is this useful? Well, suppose that you want to create a SAS/IML module that prints
In response to my recent post about how to use the PALETTE function in SAS/IML to generate color ramps, a reader wrote the following: The PALETTE function returns an array of hexadecimal values such as CXF03B20. For those of us who think about colors as RGB values, is there an
Double, double toil and trouble; Fire burn, and caldron bubble. Macbeth, Act IV, Scene I For the cyptanalyst or recreational puzzle solver, "double double" does not lead to toil or trouble. Just the opposite: The occurrence of a double-letter bigram in an enciphered word puzzle is quite fortunate. Certain double
Have you ever looked as a statistical graph that uses bright garish colors and thought, "Why in the world did that guy choose those awful colors?" Don't be "that guy"! Your choice of colors for a graph can make a huge difference in how well your visualization is perceived by
In a previous article I introduced the HEATMAPCONT subroutine in SAS/IML 13.1, which makes it easy to visualize matrices by using heat maps with continuous color ramps. This article introduces a companion subroutine. The HEATMAPDISC subroutine, which also requires SAS/IML 13.1, is designed to visualize matrices that have a small
In last week's article about the distribution of letters in an English corpus, I presented research results by Peter Norvig who used Google's digitized library and tabulated the frequency of each letter. Norvig also tabulated the frequency of bigrams, which are pairs of letters that appear consecutively within a word.
While at JSM 2014 in Boston, a statistician asked me whether it was possible to create a "customized bin plot" in SAS. When I asked for more information, she told me that she has a large data set. She wants to visualize the data, but a scatter plot is not
The skewness of a distribution indicates whether a distribution is symmetric or not. A distribution that is symmetric about its mean has zero skewness. In contrast, if the right tail of a unimodal distribution has more mass than the left tail, then the distribution is said to be "right skewed"
It's time for another blog post about ciphers. As I indicated in my previous blog post about substitution ciphers, the classical substitution cipher is no longer used to encrypt ultra-secret messages because the enciphered text is prone to a type of statistical attack known as frequency analysis. At the root
