The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs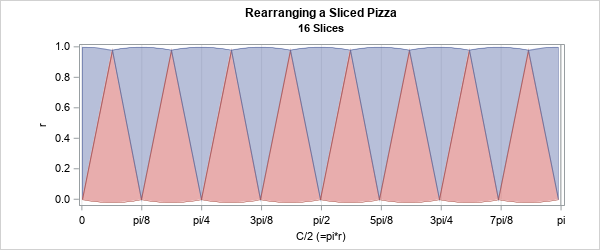
Happy Pi Day! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate all things pi-related because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979.... Pi is a mathematical constant defined as the ratio of a circle's circumference (C) to its diameter (D).
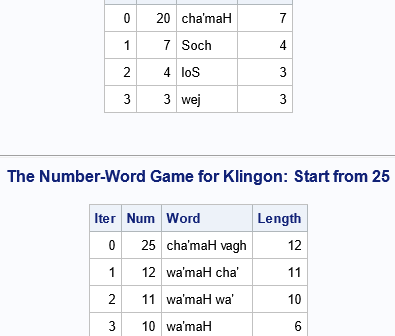
I recently wrote about the Number-Word Game, which is an iterative algorithm that generates a sequence of natural numbers by using the lengths of the words for the numbers. In English, the words are "one", "two", "three", and so on. You can play the Number-Word Game in any alphabetic language

Have you heard about the Number-Word Game? This is a simple game that has the following rules: Start with any positive integer. Write down the English word for the integer. Count the number of letters in the word. This gives a new positive integer. Go to (2). Repeat until a
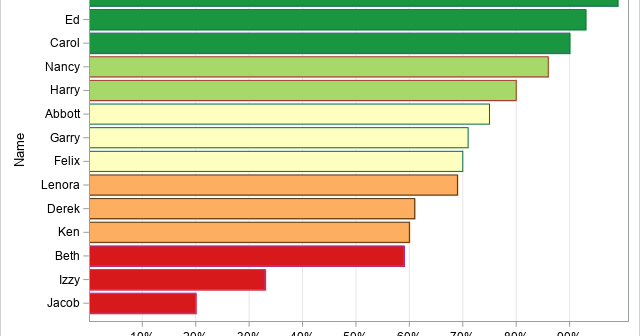
I sometimes see analysts overuse colors in statistical graphics. My rule of thumb is that you do not need to use color to represent a variable that is already represented in a graph. For example, it is redundant to use a continuous color ramp to represent the lengths of bars
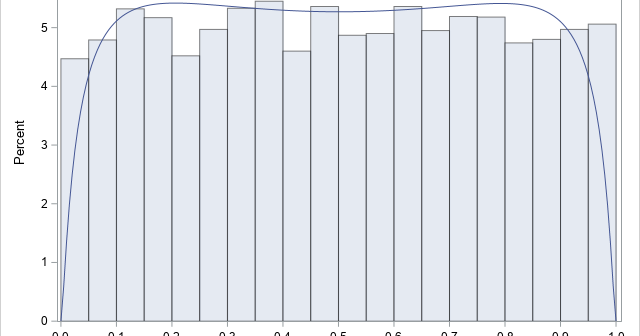
With four parameters I can fit an elephant. With five I can make his trunk wiggle. — John von Neumann Ever since the dawn of statistics, researchers have searched for the Holy Grail of statistical modeling. Namely, a flexible distribution that can model any continuous univariate data. As the quote
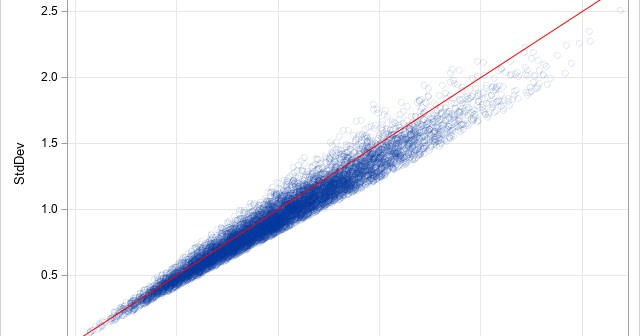
In statistical quality control, practitioners often estimate the variability of products that are being produced in a manufacturing plant. It is important to estimate the variability as soon as possible, which means trying to obtain an estimate from a small sample. Samples of size five or less are not uncommon
