In a previous post, we explored the intricacies of panel data regression. We unveiled a range of panel models and demonstrated their application in estimating cigarette demand by using the CPANEL procedure. However, achieving reliable insights in the realm of panel data regression requires addressing practical challenges. These would include such things as the potential heteroscedasticity and serial correlation among observations within the same panel unit. In this post, we will continue to use the cigarette demand example. We will delve into the critical task of generating robust standard errors for one-way fixed-effect models. This will all be within the framework of PROC CPANEL. So, prepare to delve into the depths of statistical robustness as we navigate this important aspect of panel data analysis.

Heteroscedasticity-Consistent standard errors

In panel data regression, the default classical standard errors are computed under the assumption of homoscedasticity. This means that the conditional variance of the error term is assumed to be constant and does not depend on the observed variables. However, this assumption is rarely valid in real-world scenarios. It can result in underestimated standard errors and thus spuriously high significance due to an inflated t-statistic.  For instance, in our cigarette demand analysis, US states with a higher per capita income tend to exhibit greater fluctuations in per capita cigarette sales. In this context, assuming uniform volatility across all the US states becomes unreasonable.

By using PROC CPANEL, you can leverage the HCCME= option in the MODEL statement to obtain heteroscedasticity-consistent (HC) standard errors. HCCME here represents the HC Covariance Matrix Estimation. This option offers a range of values from 0 to 3, which in a sense indicates how conservative the standard errors can be. HCCME=1 stands out as a widely employed setting in practice. It adjusts for the loss of degrees of freedom, making it a robust choice. Meanwhile, the HCCME=2 and HCCME=3 standard errors take a more conservative approach by incorporating standardized and predicted residuals, respectively. As a result, they tend to be larger compared to HCCME=0 standard errors. For more technical details, please refer to the HCCME documentation.

For our cigarette demand analysis, Figure 1 provides the SAS code. This code estimates a one-way fixed-effects model by using HC standard errors and cluster-robust standard errors. These will be discussed in the following section. Figure 2 offers an output table showcasing these robust estimates. These options can be applied similarly to other models, yielding valuable insights into your data.

proc cpanel data = mycas.Cigar; 
   id State Year;
   classical:  model LSales = LSales_1 LPrice LDisp LMin / fixone;
   hccme_0:    model LSales = LSales_1 LPrice LDisp LMin / fixone hccme=0;
   hccme_1:    model LSales = LSales_1 LPrice LDisp LMin / fixone hccme=1;
   hccme_2:    model LSales = LSales_1 LPrice LDisp LMin / fixone hccme=2;
   hccme_3:    model LSales = LSales_1 LPrice LDisp LMin / fixone hccme=3;
   cluster_1:  model LSales = LSales_1 LPrice LDisp LMin / fixone hccme=1 cluster;
   compare / mstat(none) pstat(estimate stderr probt);
run;

Figure 1: SAS PROC CPANEL code using robust standard errors

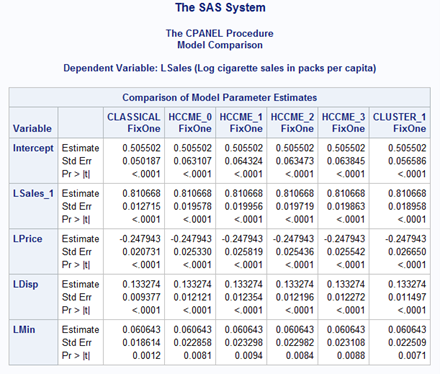
From Figure 2, it is intriguing to note that the HCCME=1 standard errors turn out to be the largest for each coefficient estimate, whereas the classical standard errors prove to be the smallest. According to Stock and Watson (2008), the HC standard errors are generally biased in panel models unless the errors are homoscedastic. In practice, this is rarely the case. This underscores the necessity for more resilient techniques to accommodate potential correlations in panel data. We refer specifically to the cluster-robust standard errors we present in the following section.

Cluster-Robust standard error

Observations for the same individual over time are often correlated with panel data. In the previous post, the first-difference model was introduced as a technique that can, to some extent, address this issue. This is particularly true when the errors follow a random walk. However, for scenarios where you need to account for arbitrary correlations within a given unit, there is another valuable tool at your disposal. This tool is the cluster-robust standard error.

By combining the CLUSTER option with HCCME= in the MODEL statement, you can obtain robust standard errors that are clustered at the individual level. Interestingly, when we delve into column CLUSTER_1 in Figure 2, we discover that clustering does not necessarily lead to significantly larger standard errors. In fact, for this specific example, they only exhibit a slight increase compared to the classical standard errors. However, they are smaller than all the other HC standard errors without clustering.

In the context of cluster-robust inference, it is crucial to recognize that the number of clusters represents the effective sample size. In our specific example, this translates to the number of states we included, which amounts to a mere 46. This underscores the importance of having a reasonably sized number of clusters when considering cluster-robust methods. It is also worth emphasizing that cluster-robust techniques are not universally preferable. Their utility varies, especially when confronted with a large number of regressors, which can result in reduced degrees of freedom and imprecise covariance estimates. In such cases, the applicability of cluster-robust methods may not be as clear-cut. For a deeper understanding of cluster inference, Econometrics by Bruce Hansen is recommended. Additionally, if you are seeking a practical guide, A Practitioner's Guide to Cluster-Robust Inference offers valuable insights on this subject.

Summary

In panel data analysis, the importance of robust standard errors cannot be overstated. Cluster-robust standard errors have become increasingly prevalent in contemporary economic applications. They play a pivotal role in safeguarding the reliability of our statistical inferences, shielding them from practical challenges like heteroscedasticity and correlated observations. If you are eager to explore additional functionalities within PROC CPANEL, online documentation is available. There, you will find a wealth of information to further enhance your panel data analysis skills and elevate your data-driven decision-making.