Collaborative filtering and supervised learning are popular methods for building modern recommender systems. Recommender systems are a technology used ubiquitously in web services including Amazon, Netflix, and Pandora. From the perspective of users, a recommender provides personalized recommendations by helping users to find interesting items. These would include things such as products, movies, and songs. From the perspective of items, a recommender produces targeted advertisements by identifying potential users that would be interested in a particular item. That is, alerting potential users to a new product, movie, song, and so on.
The information about users/items and the users’ responses or feedback to items constitute the data used to achieve the goal of recommenders. A user response can be provided explicitly as a numeral rating or a like/dislike type of feedback. Or it can be provided implicitly as a positive action. Actions such as “purchasing a product” on Amazon, “watching a movie” on Netflix, or “listening to a song” on Pandora.
Both collaborative filtering and supervised learning have their strengths and drawbacks. Is it possible to bring these two seemingly different methods together? In this post, we discuss their relations and explore the possibility of incorporating them into a unified framework. The goal will be to show you how to combine the strengths and overcome the drawbacks.
Collaborative Filtering
Collaborative filtering is based on the following intuitions:
- Users having similar views on an item are likely to share views on other items.
- Items that are similar are likely to receive similar views from a user.
For example, a simple recommender based on intuition 1 can recommend to Susan titles by Charlotte Brontë. This is based on if both she and Jennifer have read books by Louisa May Alcott and Jane Austen and if Jennifer also likes Brontë. Similarly, a simple recommender based on intuition 2 can recommend other classic titles to a customer if the customer has bought classic books in the past.
By analyzing the views of many users on many items, collaborative filtering can identify the users who share similar views on items and the items that receive similar views from users.
A straightforward way of implementing collaborative filtering is K Nearest Neighbors (KNN). For a given user, KNN recommends items liked by others who share similar views with the user on certain other items. KNN enjoys popularity due to its simplicity and ease of providing interpretable recommendations.
An alternative approach to KNN that has gained popularity in practice is matrix factorization (MF). An illustration of MF is given in Figure 1. R is a matrix that represents users’ responses to items, with each row corresponding to a user and each column to an item. Each * indicates an observed response, and the missing entries correspond to the unobserved responses. The response matrix is approximated as a product of two factor matrices, R=XY, where the rows of X and the columns of Y embed users and items, respectively, into a Euclidean space.
With this embedding, each user or item is represented by a vector. Each user’s response to an item is represented by the inner product of two vectors. These vectors can be considered as a feature representation of the users and items. As they are not observed but rather are learned from the observed user-item interactions, these vectors are commonly referred to as latent features or factors.
In contrast to KNN, which is a local model that gleans information from neighbors only, MF is a global model that extracts information from all users and all items. As a result, the feature vector of each user is not only influenced by its own interaction history but also by the interaction histories of other users. This includes the extent of influence dictated by the similarity between users. For this reason, a user might discover new interesting items from the interaction histories of its peers who share similar interests, with the similarity identified from all users’ interaction histories by learning algorithms.
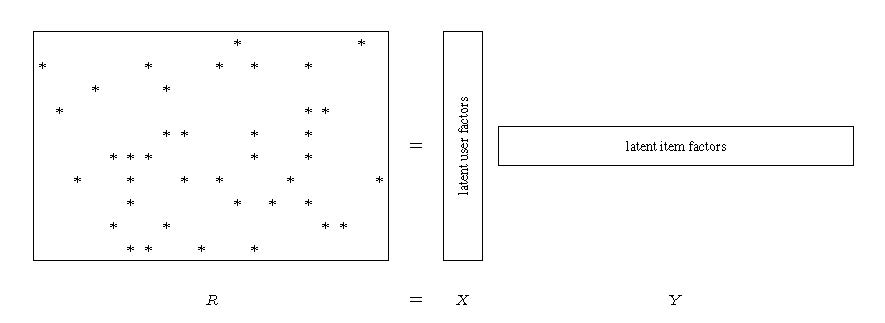
The MF model can be learned by Alternating Least Squares (ALS). ALS updates the two factor matrices X and Y alternately, keeping one fixed while updating the other.
Supervised Learning
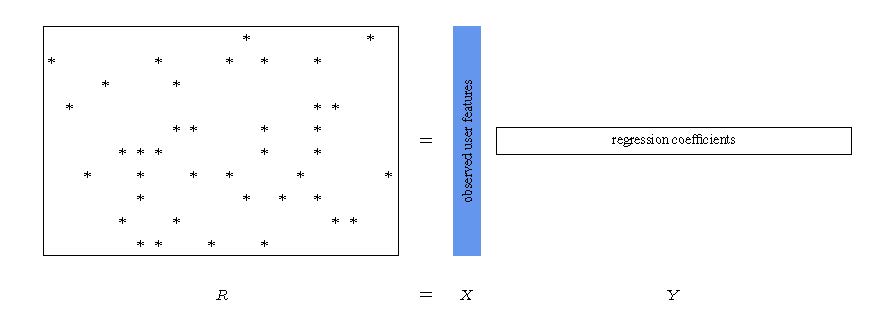
When ALS is used to learn the MF model, it applies two instances of supervised learning in each iteration. One for solving X for given Y, and the other for solving Y for given X. What happens if X holds observed features of users and therefore isn't adjustable? Then clearly you are spared the need to alternate between X and Y, as the whole problem becomes supervised learning of Y given X is the data.
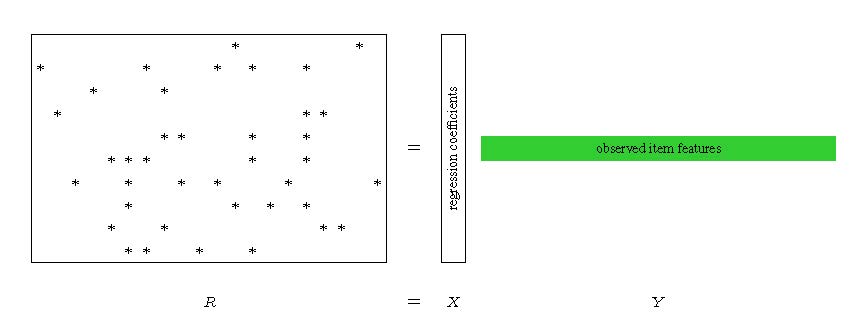
Similarly, when Y holds observed features of items and is not adjustable, the whole problem becomes supervised learning of X given Y is the data. These two cases are illustrated in Figures 2 and 3. One factor matrix serves as data, and the other serves as the parameters of a linear model.
Collaborative Filtering Meets Supervised Learning
Collaborative filtering simultaneously learns on many users and items to take advantage of the between-user and/or between-item similarities. However, it has to cold-start the model for new users/items due to a lack of information about the newcomers.
In the case of supervised learning, it learns the model of each user/item independently, in ignorance of the between-user and/or between-item similarities. But it can provide personalized recommendations to new users/items by using the observed features of the newcomers.
Is it possible then to get the benefits of both models and yet avoid their drawbacks? Indeed, an affirmative answer has been given. A hybrid recommender model, termed Matrix Factorization with Partially Defined Factors (MF-PDF), was constructed to combine the benefits of supervised learning and collaborative filtering while avoiding the drawbacks.
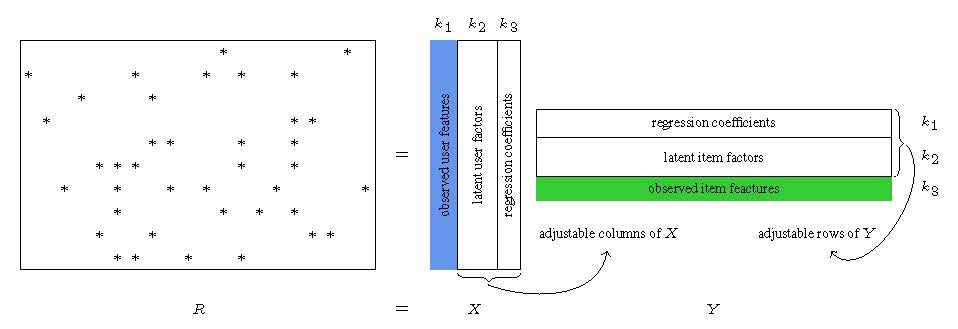
The MF-PDF model is illustrated in Figure 4. The new model is an integration of the MF model in Figure 1 with the two supervised-learning models in Figures 2 and 3. In particular, the X matrix in Figure 4 is composed of the X matrices in Figures 1, 2, and 3. The Y matrix in Figure 4 is composed of the Y matrices in Figures 1 through 3. It is noted that the user features are prefixed to X while the item features are suffixed to Y; this particular arrangement is to facilitate efficiency in storage and computation.
Alternatively, the new model might be viewed as extending the MF model in Figure 1 to allow a subset of columns of X (highlighted in blue) and/or a subset of rows of Y (highlighted in green) to be predefined and fixed. The predefined columns of X (or rows of Y) induce linear models whose parameters are contained in the corresponding rows of Y (or columns of X).
The integrated model is versatile and subsumes various sub-models as its special cases. This is shown in Table 1. Two important cases are particularly noted. One is when k1=k3=0, the MF-PDF model boils down to standard MF. The second is when k2=0, the model becomes a combination of two supervised-learning models, one on observed user features and the other on observed item features.
| k1 | k2 | k3 | Sub-model |
| 0 | >0 | 0 | MF |
| 1 | >0 | 0 | MF + item bias |
| 0 | >0 | 1 | MF + user bias |
| 1 | >0 | 1 | MF + user/item biases |
| 1 | 0 | >1 | Supervised learning on item features + user/item biases |
| >1 | 0 | 1 | Supervised learning on user features + user/item biases |
| >1 | 0 | >1 | Supervised learning on user and item features + user/item biases |
| 1 | >0 | >1 | MF + supervised learning on item features + user/item biases |
| >1 | >0 | 1 | MF + supervised learning on user features + user/item biases |
| >1 | >0 | >1 | MF + supervised learning on user/item features + user/item biases |
Implementation in the SAS Event Stream Processing Recommender
The MF-PDF model has been implemented in the streaming recommender of SAS Event Stream Processing. The recommender supports various algorithms for training the MF-PDF model on explicit or implicit feedback. These includes DAOS, softImpute-ALS, DTOS, and AWLS. Moreover, both batch-mode training and online training are supported.
The streaming recommender uses five parameters in XML to specify the sub-models of MF-PDF. The five XML parameters are: hasUserBias, hasItemBias, nUserObs, nFactors, and nItemObs. They specify the sub-models in the way shown in the Table 2, where buser=0 if hasUserBias=0 and buser=1 otherwise, bitem=0 if hasItemBias=0 and bitem=1 otherwise.
| Sub-model dimension | k1 | k2 | k3 |
| Specification in XML | nUserObs+buser | nFactors-buser-bitem | nItemObs+bitem |
The following is a snippet of an example XML specification.
This translates into k1=3, k2=1, k3=4, and the sub-model specified is ‘MF + supervised learning on user/item features + user/item biases”.
The observed user/item features are provided to the streaming recommender through a list of fields. This is shown as i1, i2, i3, i4, i5 in the following snippet.
The list is split into two sub-lists in the way shown in the following table. One sub-list is for user features. The other one is for item features.
Unique Advantages of MF-PDF Models
The MF-PDF models integrate user/item features into feedback data in a unique way. They are different from other feature-enhanced approaches such as a factorization machine and a matrix factorization with side information. More specifically, each user in MF-PDF has free linear parameters for item features. So does each item for user features. By contrast, the user/item features in a factorization machine are restricted to having a factorized form of parameters. Matrix factorization with side information does not even have linear parameters for user/item features.
Moreover, MF-PDF offers advantages for software implementation of the model and the associated learning algorithms. In particular, the arrangement of observed user/item features (aka predefined factors) in MF-PDF has been designed to take advantage of the efficiency of in-memory access and computation. To make this point clearer, we first note the parameters of MF-PDF are conveniently represented by submatrices of X and Y. This is because the user features are prefixed to X. And the item features are suffixed to Y. With this particular storage for X and Y, the supervised-learning models and the collaborative-filtering model can be updated efficiently in a joint manner.
Conclusions
Collaborative filtering with an MF model aims to find the latent features of users and items. By appending observed features to the latent features, the MF model is generalized to a hybrid model (MF-PDF). This blends supervised learning seamlessly into collaborative filtering. The way in which the observed features are appended makes MF-PDF particularly efficient in storage and computation. That is, the user features are prefixed to X while the item features are suffixed to Y. The MF-PDF model integrates user/item features into feedback data in a unique way that is different from other feature-enhanced approaches such as factorization machine and matrix factorization with side information. The model has been implemented in the SAS Event Stream Processing streaming recommender, supporting various algorithms for training the model on explicit feedback or implicit feedback.
LEARN MORE | MACHINE LEARNING ALGORITHM CHEAT SHEET









