Parte II: Partial Dependence Plots
Repasemos como llegamos hasta acá. Desde hace varios años los algoritmos de machine learning nos ofrecen una mejora sustancial en sus capacidades, son cada vez más precisos. Además, gracias a la optimización hiperparamétrica, el analista puede utilizar el tiempo de prueba y error que le tomaba configurar los algoritmos en otros problemas de mayor importancia.
Pero estos avances vinieron acompañados de un aumento en su complejidad que los volvió muy difíciles de interpretar por humanos. No poder interpretarlos reduce la confianza en los mismos y oculta posibles errores en los datos o en el diseño de éstos. Incluso cuando no hay errores, los algoritmos podrían estar teniendo sesgos étnicos o de género no deseados, como vimos en el artículo anterior.
Para luchar con estos problemas, aparecieron métodos que ayudan interpretar la forma en la que los modelos predicen. En el artículo anterior empezamos a explorar estos métodos modelando un churn de empleados con dos modelos: un gradient boosting y una red neuronal.
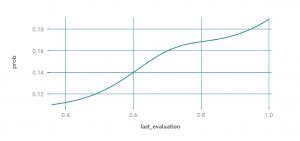
En el artículo anterior vimos el método (global) PDP, que refleja el aporte de una variable a la predicción. Por ejemplo, si queremos analizar el aporte de la variable puntaje de su última evaluación (last_evaluation), vemos que a mayor puntaje obtenga en su evaluación, mayor es la probabilidad de que el colaborador se vaya.
A esta altura, con solo ver la gráfica, no es necesario decir a cuál de nuestros dos modelos pertenece, ¿no?
Sin embargo, ¿Es posible aplicar este comportamiento que refleja nuestro modelo a todos los empleados? ¿Podrá el modelo identificar si hay empleados que tienen un comportamiento distinto? Algunos ejemplos podrían ser: empleados que con una evaluación baja les aumente la probabilidad de irse o que un buen resultado en la evaluación los motive a seguir en la compañía.
Para responder como afecta una variable sólo para un individuo (y no para todos los casos), podemos usar el siguiente método:
Individual Conditional Expectation (ICE)
Tomamos una variable para analizar, como hacemos con PDP, pero en vez de analizarla con la población entera, el ICE sólo la analiza con respecto a una observación (que en nuestro problema de negocio representa un colaborador). Por esta razón, diremos que ICE es un método de interpretación local. Entonces, se puede pensar en cada curva de ICE como una especie de simulación que muestra lo que pasaría con la predicción del modelo si variara una característica de un individuo en particular. Esto es algo muy interesante, ya que nos puede dar un norte sobre qué acción realizar para cambiar el pronóstico (siempre que tenga sentido y sea posible). Por ejemplo, si la edad de un empleado es una variable importante para nuestro modelo y vemos que con 15 años más el mismo tendría menor probabilidad de irse, poco podemos hacer (o al menos sin usar extrañas artes místicas o conjuros de dudosa validez ética). Sin embargo, si el empleado es bueno y tiene una alta propensión de abandonar la empresa, pero nuestro modelo nos advierte que de tener un aumento de sueldo su probabilidad de irse es considerablemente menor, quizás anticiparse al problema y darle un merecido aumento puede ser la mejor inversión, teniendo en cuenta todos los costos asociados a la pérdida de un valioso colaborador.
Para empezar a explorar la técnica ICE vamos a necesitar casos para analizar. Como estamos trabajando con casos no nominados, en vez de tomar casos al azar, vamos a segmentar la población con un kmeans de 10 clusters y usar sus centroides como observaciones. Veamos ahora para nuestros nuevos casos como son las curvas de la última evaluación que veníamos analizando:
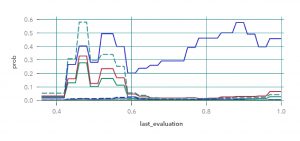
Gradient Boosting
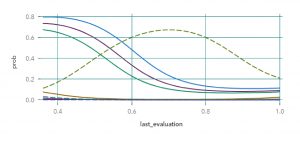
Red Neuronal
A simple vista se observa un gran cambio tomando los casos individuales. En el gráfico del gradient boosting, vemos que la mayoría de los clusters tienen un comportamiento similar excepto uno: el clúster 2, el cual marca un fuerte aumento de la probabilidad de abandono cuanto mayor puntaje tienen. Una vez perfilado el clúster, notamos que la observación representa a los empleados que tienen puntajes muy altos en sus evaluaciones, trabajan mucho más que la mayoría y tienen bajos niveles de conformidad con la empresa. El modelo de la red neuronal distingue también a ese clúster por sobre el resto (es el gráfico es la campana de gauss), pero disminuye su probabilidad en las puntuaciones más altas.
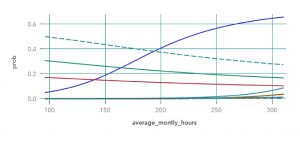
Viendo que una de las características que más representan al clúster 2 son las horas trabajadas, vamos a ver los gráficos ICE para esta variable:
Gradient Boosting
Red Neuronal
En ambos casos, la curva azul que se destaca pertenece al clúster 2, y recordando que se trata de personas con gran cantidad de horas de trabajo mensual, los dos modelos demuestran que si los empleados trabajaran menos horas, su probabilidad de abandonar la empresa disminuiría. En este caso, hay que tener en cuenta que la variable horas de trabajo es una de las variables que en la mayoría de los casos se puede controlar (al contrario de la variable edad).
Entre las curvas restantes es importante destacar que muchos clústeres tienen el mismo comportamiento, lo que plantea que los mismos se los puede reagrupar en un nuevo clúster.
Con el método ICE bajamos al nivel de la observación para analizar el comportamiento de la variable. Sin embargo, queda una crítica pendiente: lo hicimos sobre una variable a la vez. Un problema que solucionaremos en la siguiente entrega de esta serie.
Los espero.