はじめに

因果推論コラム・シリーズでは潜在アウトカムモデルに基づく因果推論の解説を行なっています。今回のテーマは操作変数法（instrmental variable methods）です。

ある介入AがアウトカムYに及ぼす平均因果効果を推定する手法の1つに操作変数法があります。この手法は、操作変数と呼ばれる変数を利用することで交絡因子を調整することなく平均因果効果を推定する手法です。分野や状況によって交絡因子の特定や測定は困難であることは多く、それらの調整を行う必要がないという点で操作変数法は魅力的な手法です。ただ一方で、共変量調整に基づく因果効果の推定手法では必要とされない仮定が要求されますので、その点ご注意ください。ある変数が操作変数であるための条件は以下の3つです。各条件の詳細や実際にどのような変数が操作変数として提案されているか、操作変数と介入変数の相関が弱い場合に発生する問題については前回のコラムをご参照ください。

1. ZはAと関連する
2. ZはYに対してAを介した以外の効果を持たない
3. ZとYは共通原因を持たない

一般的な誤解として、操作変数法では操作変数が存在さえしていれば平均因果効果の推定が可能であるという認識があります。厳密には、操作変数が存在している場合に操作変数法によって推定可能なのはboundsと呼ばれる平均因果効果が含まれる幅であり、平均因果効果を推定するためには後述する仮定のいずれかが成立している必要があります。また、操作変数に関する3条件に加えて第4の条件としてどちらの仮定を置くかによっても、どのような集団における平均因果効果が推定可能であるかが異なります。本コラムではboundsと呼ばれる因果効果の部分識別について紹介した後、平均因果効果の識別に必要となるhomogeneity、およびmonotonicityについて紹介をします。なお、boundsは信頼区間とは異なる概念であることにご注意ください。

 

Bounds：因果効果の部分識別

このセクションでは本コラムシリーズの参考書籍である『Causal Inference: What If』の具体例を一部改変し、boundsについて簡単に紹介していきます。

「集団全員にある介入を行なった場合、行わなかった場合と比較して加法的なスケールで平均的にどの程度効果があるか」を示す平均因果効果E[Y^a=1]-E[Y^a=0]は、二値アウトカムに関してはPr[Y^a=1=1]-Pr[Y^a=0=1]と表すことが可能です。ここで、このPr[Y^a=1=1]-Pr[Y^a=0=1]のとりうる値の下限と上限を考えてみると、集団の潜在アウトカムに関して無情報である場合（データが何も存在しない場合）には、当然のことですが、下限は-1、上限は1です。

• Pr[Y^a=1=1]-Pr[Y^a=0=1]=-1（下限）
  • Pr[Y^a=1=1]=0：介入を受ける場合の潜在アウトカムはすべての被験者に関して0
  • Pr[Y^a=0=1]=1：介入を受けない場合の潜在アウトカムはすべての被験者に関して1
• Pr[Y^a=1=1]-Pr[Y^a=0=1]=1（上限）
  • Pr[Y^a=1=1]=1：介入を受ける場合の潜在アウトカムはすべての被験者に関して1
  • Pr[Y^a=0=1]=0：介入を受けない場合の潜在アウトカムはすべての被験者に関して1

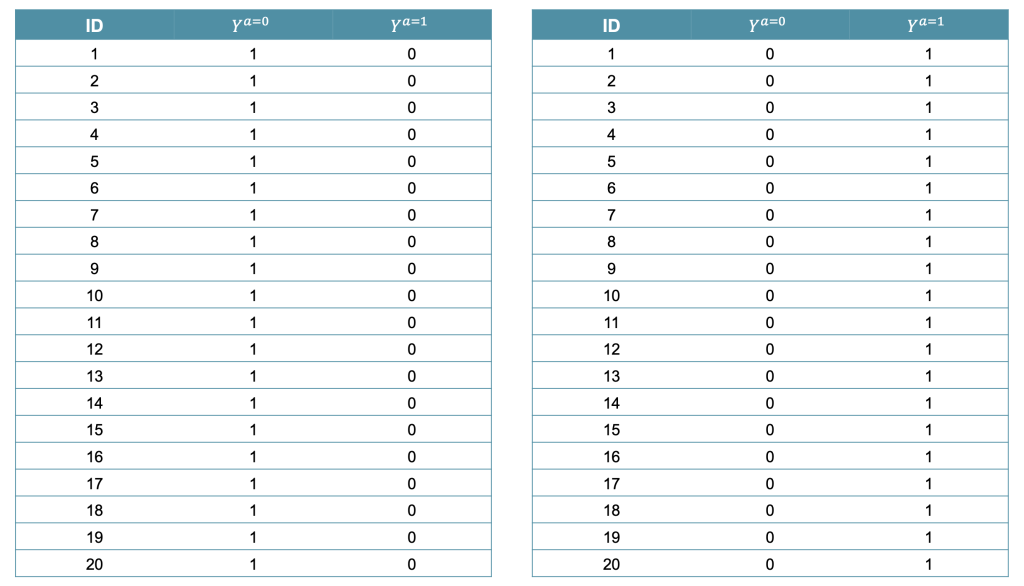
すなわち、二値アウトカムに対する無条件での平均因果効果が含まれる幅（bounds）は[−1,1]です。例えば、集団が20名で構成されているとすると、下限と上限になる潜在アウトカムの状況は下図の通りです。

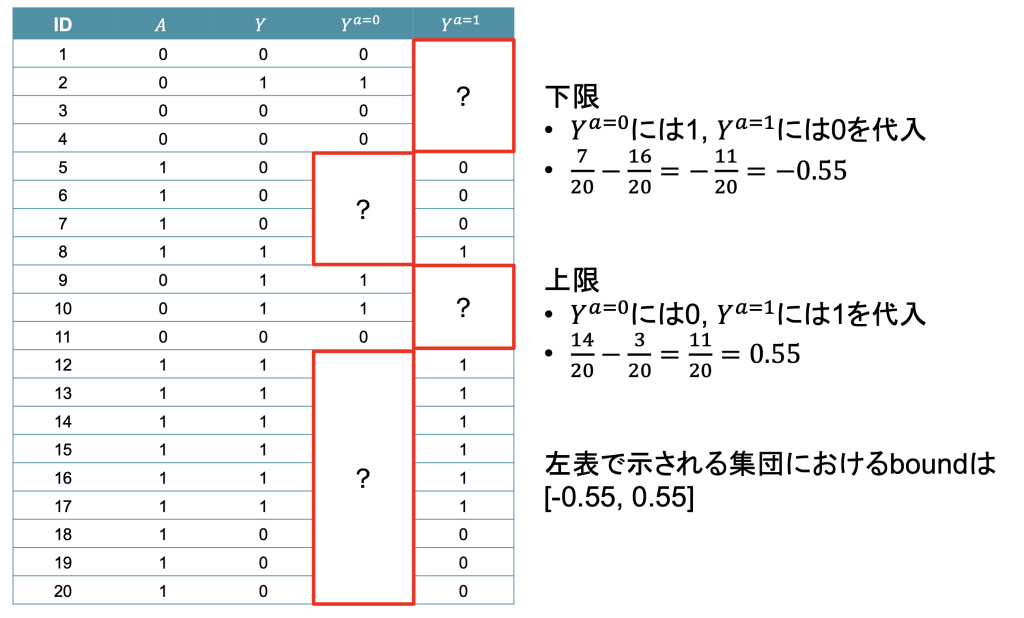
ここで集団（の一部）に関して実際にデータが得られた時、一致性の下でboundsはより狭く考えることが出来ます。これは、データとして一部の被験者らの潜在アウトカムY^a=1, Y^a=0の情報が得られるため、未知の部分に対して最も極端な場合の値を代入することによって下図のように下限と上限を計算することが出来ます。

なお、アウトカムが二値変数ではなく連続変数である場合にboundsを計算するためには、アウトカムが取り得る最小値と最大値を指定し、二値変数の場合と同様に代入する必要があります。また余談ですが、boundは前回のコラムで紹介した集団レベルでの除外制約 (condition (ii)) とmarginal exchangeability (condition (iii)) が成立する操作変数Zが存在する場合にはboundsをより狭く考えることが可能です。この場合のboundsはnatural boundsと呼ばれ、その幅はPr[A=1|Z=0]+Pr[A=0|Z=1] となり、データのみから識別されるものよりも狭くなります（Robins 1989, Manski 1990）。加えて、marginal exchangeabilityではなくjoint exchangeabilityが成立する場合には、さらに狭い幅となるsharp boundsを識別することが可能です。さらに追加の仮定を置くことでより狭いboundsが計算することができることも示されています（Richardson, Evans and Robins 2011）。しかし、上記のようなboundsは、一般には因果効果として用いる指標のnull value（e.g., E[Y^a=1-Y^a=0] であれば0）を含むかなり広い幅となり、有用でないことの方が一般的です。

 

第4の仮定：homogeneity（同質性）

操作変数であるための3条件に加え、AのYへの効果に対しパラメトリックな仮定を置き、さらにこのセクションで紹介するhomogeneity（同質性）の仮定が成立する場合には、boundsの下限と上限はある値に収束し平均因果効果E[Y^a=1-Y^a=0] を点推定することが可能です。ここでは、歴史的に登場した順に、4つのバージョンのhomogeneityを紹介していきます。

• バージョン①

最も古くに提案されたhomogeneityは、介入AのアウトカムYへの因果効果が個人間で一定（定数）であるということを指すものです。また、効果が個人間で一定であるということは、潜在アウトカムY^a=0, Y^a=1をそれぞれその大きさによって並び替えた際に、Ya=0とYa=1の並びが同じであることを意味しますので、このhomogeneityはadditive rank preservationと同義です。なお、二値アウトカムに関してはsharp null（全員の値が0→0と一切変化しない）、またはuniversal harm/benefit（全員の値が0→1 or 1→0と変化）することを意味しています。しかし、ある介入を行った時介入の効果が現れる人、現れない人、またその効果の程度も通常は個人差があるため、このhomogeneityの成立を認めることはあまり合理的ではありません。

• バージョン②

2つめのhomogeneityのバージョンは、介入AとアウトカムYが共に2値変数である場合、介入群 (A=1) と対照群 (A=0) における平均因果効果が操作変数Zの水準間で一定であるというものです。これは、操作変数も二値である場合には以下の等号成立を仮定するものです。

E[Y^a=1−Y^a=1|Z=0,A=a]=E[Y^a=1−Y^a=1|Z=1,A=a] for a=0,1

先ほどのhomogeneityと比較すると多少現実的に見受けられますが、仮に潜在アウトカムと操作変数が独立（Y^a⊥Z）であった場合であっても、一般に介入Aでの条件付き独立Ya⊥Z|Aは成立しません。したがって、介入の効果はZに依存する可能性があるため、このhomogeneityは成立しない可能性があります。そこで一貫して検証不可能な仮定であることには変わりがないものの、より現実的なhomogeneityとして提案されたのが次のバージョンになります。

• バージョン③

3つ目に紹介するhomogeneityは、特定（未測定でも可）の交絡因子Uによる効果修飾に関する効果の同質性を指すものです。すなわちUが加法的な効果修飾因子でないこと、介入AのアウトカムYへの平均因果効果というのが未測定交絡因子Uのいずれの水準においても同じであることです（E[Y^a=1|U]−E[Y^a=0|U]=E[Y^a=1]−E[Y^a=0]）。ただ当然のことですが、効果修飾因子となる未測定の交絡因子が存在する可能性は常にありますので、このhomogeneityもしばしば非現実的な仮定とみなされます。

• バージョン④

最後に紹介するhomogeityは、加法的なスケールでのZとAの関連が未測定交因子の水準間で一定であるというもので、数式としては以下の内容です。

E[A|Z=1,U]−E[A|Z=0,U]=E[A|Z=1]−E[A|Z=0]

このhomogeneityと、先ほどのhomogeneity (E[Ya=1|U−E[Ya=0|U]=E[Ya=1]−E[Ya=0]) は、介入AのアウトカムYへの因果効果におけるUによる効果修飾 (e(u)) が、加法的なスケールでのZとAの関連のUによる修飾 (t(u)) とは無相関である (Cov(e(u),t(u))=0) 、というより一般的な条件の特殊なケースにあたります。これはバージョン②ではe(u)を、バージョン③ではt(u)を定数としたものとみることができ、変数と定数の共分散は常に0となることによるものです。

e(u)≡E[Ya=1−Ya=0|U]
t(u)≡E[A|Z=1,U]−E[A|Z=0,U]

 

ここまで4つのhomogeneityを紹介しましたが、程度の差は多少あるにしろ、多くの状況でいずれのhomogeneityもその成立を仮定することは非現実的です。したがって、操作変数法による平均因果効果の推定は、提案した変数が操作変数たりうるものかといったことと相まってしばしば懐疑的に見れらます。そこで、homogeneityに依存しない以下の2つのアプローチが提案されています。本コラムでは、homogeneityとは異なる仮定に依存するアプローチを紹介します。

1. homogeneityではなく成立がより妥当であるとみなせるmonotonicityという仮定を置く
2. 操作変数法による推定の際のモデルにベースライン共変量を含める

 

第4の仮定： monotonicity（単調性）

homogeneityの代わりに置かれる仮定は、monotonicity（単調性）と呼ばれるものです。先に結論を述べますと、monotonicityはhomogeneityよりも比較的成立を認めることが妥当な仮定ですが、homogeneityを操作変数法の第4の条件として用いた場合には、操作変数の3条件が成立していたとしても集団における平均因果効果は推定できません。すなわち、monotonicityを用いた場合には推定対象が平均因果効果とは異なり、得ることが可能なのは局所平均治療効果 (LATE; Local Average Treatmen Effect) と呼ばれる特定の部分集団における平均因果効果の推定値になります。

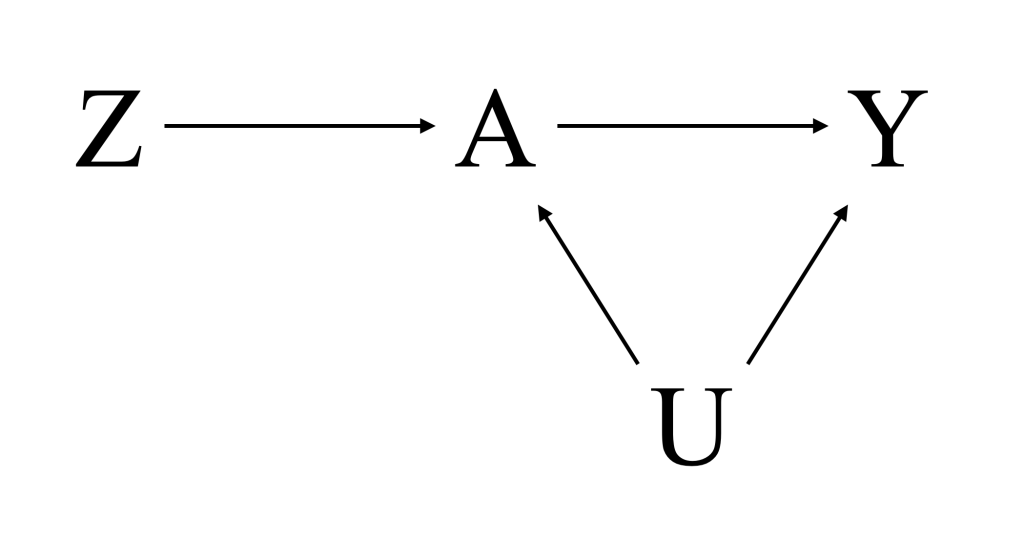
まず、monotonicity（単調性）を紹介するにあたり前回のコラムでも扱いました以下のDAGで示される二重盲検プラセボ対照ランダム化試験を再度考えます。

• Z：ランダム割付変数（1：介入群、0：対照群）
• A：実際に受けた介入（1：介入あり、0：介入なし）
• Y：アウトカム（1：イベントの発生、0：イベントの未発生）
• U：AとYに影響を及ぼす全ての共変量、AとYのcommon cause（未測定の共変量を含む）

次にアウトカムと同様に、各個人の介入に対する潜在変数A^zを考えます。ここでA^z=1は介入群に割り付けられた場合 (Z=1) にその個人がとる介入の値、A^z=0は対照群に割り付けられた場合 (Z=0) にある個人がとる介入の値を意味し、それぞれ0,1をとります。

• A^z=1：介入群に割り付られた場合の潜在介入変数
  • A^z=1=1：介入群に割り付られた場合には介入を受ける
  • A^z=1=0：介入群に割り付られた場合には介入を受けない
• A^z=0：対照群に割り付られた場合の潜在介入変数
  • A^z=0=1：対照群に割り付られた場合には介入を受ける
  • A^z=0=0：対照群に割り付られた場合には介入を受けない

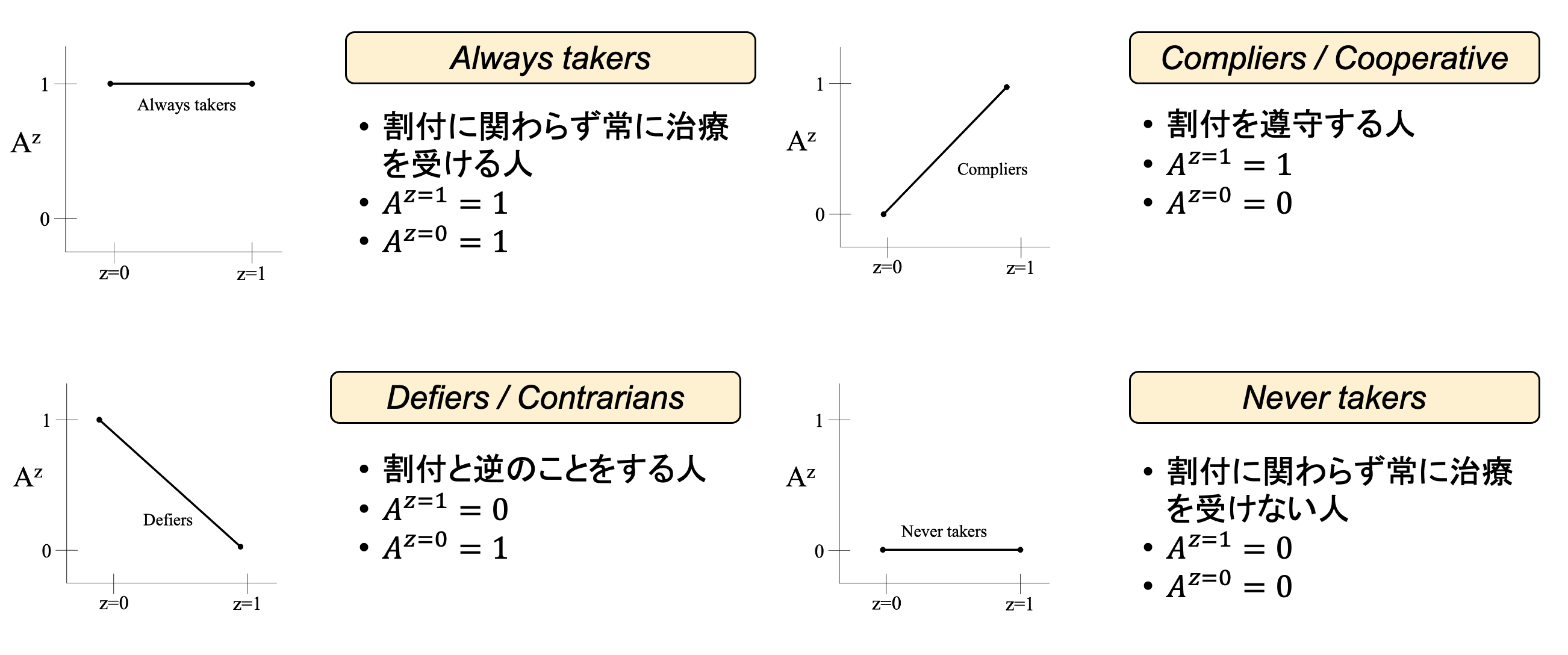
そしてこの2つの潜在変数の値を仮に知ることができたとすると、その値の取り方から研究集団に属する個人をcompliance typesやprincipal strataとも呼ばれる次の4つの部分集団※1に分類することが可能です。

• Always takers
  • 割り付けに関わらず常に介入を受ける集団
  • A^z=1=1,A^z=0=1
• Never takers
  • 割付に関わらず常に介入を受けない集団
  • A^z=1=0,A^z=0=0
• Compliers (Cooperative)
  • 介入群に割付けられた場合には介入を受け、対照群に割付けられた場合には介入を受けない集団（割付結果を完全に遵守する集団）
  • A^z=1=1,A^z=0=0
• Defiers (Contrarians)
  • 介入群に割付けられた場合には介入を受けず、対照群に割付けられた場合には介入を受ける集団（割付結果と真逆の治療を実施）
  • A^z=1=0,A^z=0=1

定義上は各個人をこの4つの部分集団に分けることができますが、データからは個人がどの集団に属しているか識別することはできないことに注意が必要です。例えば、介入群へ割付けられ (Z=1) 、かつ実際に介入を受けた(A=1) 個人はalways takerであるのか、それともcomplierであるのか判断することはできず。同様に対照群へ割付けられ (Z=0) 、実際に介入を受けなかった (A=0) 個人はnever takerであるのか、それともdefierであるのかの判断をすることはできません。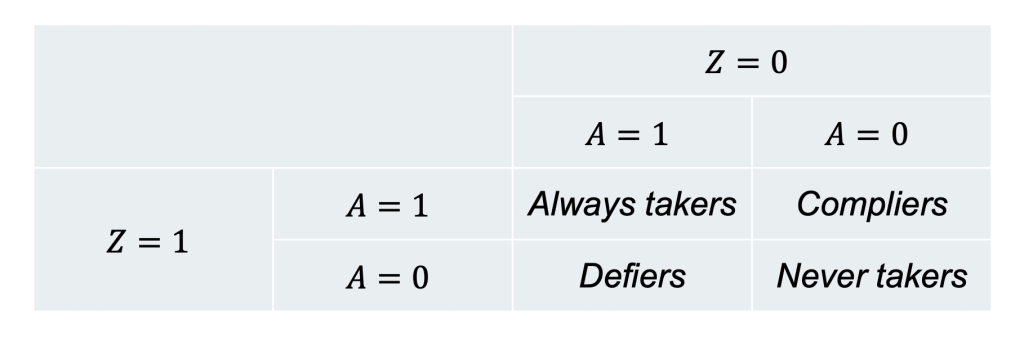

ここで仮にdefiersが存在しないとすると、下のalways takers, never takersを意味する図で示されるように操作変数Zは治療Aを変化させないか、compliersに関する図で示されるように介入Aの値を増加させるため、関数的なmonotonicity（単調性）があるということができます。より一般には、すべての個人に対しA^z=1≧A^z=0となるとき単調性が成立するといいます。なお、今回のコラムシリーズではともに二値である操作変数、治療についてのみ扱いますのでここではdefiersが存在しないという認識で構いません。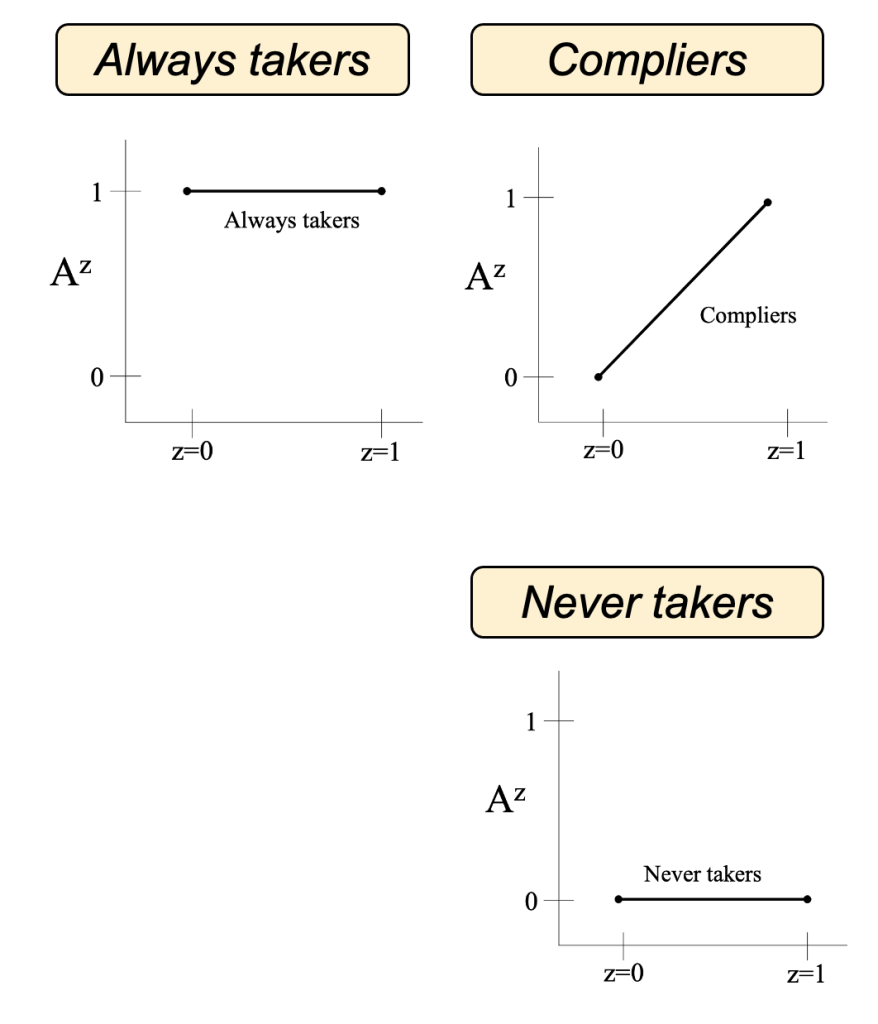上記では実験研究という状況設定をおいていましたが、観察研究においては割付という概念が存在しないため割付遵守の議論がそもそも発生せず、言葉的な意味合いとしてのdefiersもcompliersも存在しませんが、(Az=1=1,Az=0=0)となる個人をcomplier、(Az=1=0,Az=0=1)となる個人をdefierとします。ただし、ランダム化試験における割付の遵守結果との混同を避けるために観察研究においてはcompliersをcooperative、defiersをnon-cooperativeと表記する場合もあります (Gleenland, 2000) 。

 

Monotonicityに対する批判

操作変数を用いた因果効果推定の推定における第4の条件としてhomogeneityではなくmonotonicityを用いることに対しては下記のようないくつかの批判があります。

1つ目はcompliersにおける効果の関連性が懐疑的であるということです。前述のように誰がcomplierにあたるかということは識別することはできず、母集団におけるcompliersの割合は計算できるものの、その割合は研究によっても異なりますし、同一の研究内であっても用いる操作変数によって異なります。例えば、ある研究における集団の10%がcompliersでありcompliersに対しては介入が有益であるという結果が得られた時、その結果をもとにしてより大きな母集団に対して介入の実施を推奨すべきでしょうか。現実にはcompliersはもっと少ない可能性も、多い可能性もありますし、さらに母集団の大部分を占めるalways takers, never takersに対しては反対に介入がそれほど有益ではないとしたらどうでしょうか。 compliersがどの個人から構成されるかを識別することができればその集団にのみ介入を実施するという施策を考えることができますが、残念ながらそういった意思決定をすることはできません。

2つ目は、monotonicityの仮定は観察研究においては必ずしも合理的な仮定ではないことです。ランダム化試験においては、研究主導者側から言われたことと真逆のことをするという明確な意図を持って試験に参加するという個人が存在することは一般には期待されず、defiersが存在しないと仮定することは妥当であると考えられます。さらに、対照群に割り付けられた個人は試験中は介入を受けないようにされる臨床試験のような状況においては、研究デザイン上monotonicityの成立は保証されます。しかし、観察研究で提案されるいくつかの操作変数に対しては、monotonicityを正当化することは難しくなります。例えば、ある介入に対し異なる嗜好 (preference) をもつ2人の医師が勤務するクリニックに通う患者に対する介入の因果効果を推定するために「医師の嗜好」という尺度が操作変数として提案されたとします。そして1人目の医師は介入を実施することを好みますが、ある介入の既知の禁忌により糖尿病患者には治療を実施せず、反対にもう1人の医師は介入の実施を好みませんがいくつかのベネフィットから身体的な活動レベルが高い患者には例外的に介入を実施するとします。このとき問題となるのは、両者の例外的な扱いとなる患者です。すなわち、身体活動レベルが高く、かつ糖尿病である患者です。この患者は2名の医師の嗜好に反する介入を受けることになり、したがってdefierとして扱われることとなります。つまり、リスクとベネフィットの両方を含む複数の基準や奨励を加味して介入実施の決定がされる場合にはmonotonicityは成立しにくくなります。また、そのような状況においてはdefiersの割合が大きくなることは十分に想定されますので、その存在を無視することができなくなる可能性があります。

3つ目は、母集団を4つの部分集団に分割することが妥当であるかについてです。現実では、多くの状況においてcompliersという部分集団はその定義が十分ではない（ill-definedな）集団です。例えば、先ほどの例のように複数の医師が存在する状況において「医師の嗜好」という操作変数を提案した場合にcompliersを十分に定義するためには、ある患者を診察することのできる同じ嗜好レベルを持つ医師は、全く同じ方法でその患者を治療しなければならなりません。しかし、これ自体が非現実的な仮定であることに加えて、どの医師がどの患者を診察したかという対応関係がわからないたいていの観察研究においては、本質的にcompliersを定義することができません。また以前のコラムで紹介した潜在アウトカムに関する議論と同様にcompliers, defiers, always takers, never takersへの分割のためには決定論的反実仮想（平均因果効果の推定には一般に不要）、非干渉性（e.g., 基本はalways takerであるが、友人が介入を受けなかった場合には治療を受けないというようなことがない）、介入の複数のバージョンや異質性の異なる形が存在しない（ある状況や特定の操作変数に対するcomplierが他の状況でcomplierとならない）ことが必要となります。

 

おわりに

本コラムをまとめますと、操作変数法による因果効果の推定を行う場合には操作変数の3条件を満たす操作変数がまず必要となります。しかし、この時推定することができるのはboundsと呼ばれる興味のある因果効果が含まれる幅であり（i.e., 平均因果効果の部分識別のみ可能）、その幅はたいていのケースで非常に広くあまり意味をなしません。そこで、第4の条件としてhomogeneityを追加で仮定することによって平均因果効果の点推定が可能となります。しかし、homogeneityの成立を認めることは非現実的であるケースが多く、そこで推定対象が平均因果効果からcompliersと呼ばれる割付結果を遵守する集団における局所因果効果に代わるものの、よりその成立が妥当であると考えられるmonotonicityが第4の条件として置かれることがあります。

次回のコラムでは第4の条件としてhomogeneityを用いた場合の平均因果効果、monotonicityを用いた場合の局所因果効果を操作変数法によって推定することが可能な理由を数学的に説明していきます。また、その推定方法もいくつかあり、SASでの実装も踏まえて紹介を行います。