はじめに 

　前回のコラムでは因果関係を統計学的に考えるために「潜在アウトカム」という概念を導入しました。そして、因果効果を異なる介入レベルの潜在アウトカムの比較によって定義しました。例えば、心臓移植という介入がその後の生存に関して因果効果を持つかどうかを考えたい場合には、各個人が心臓移植を受けたらどうなったか、もしくは受けなかったらどうなっていたかという2つのifの結果（潜在アウトカム）を考え、それぞれを比較します。これが潜在アウトカムの枠組みでの因果推論（Rubin流の因果推論）の基本的な考え方になります。 

　しかし、詳細については後述しますが、このifの結果である潜在アウトカムは、現実にはいずれか1つしか観測はされず、もう一方は現実には得られない結果（反事実）となるため、個人における因果効果は定義することは可能であっても、その値を求めることは一般には出来ません。しかし、平均因果効果については識別可能条件 (identifiability conditions) と呼ばれる以下の3つの仮定の下では、その値をデータから推定することが可能です。   

• 一致性 (consistency)   
• 交換可能性 (exchangeability) 
• 正値性 (positivity)  

　今回のコラムではこれらが意図する内容について解説を行います。なお推定手法によっては追加の仮定や、ここで紹介したものとは異なる仮定が置かれる場合（e.g., 操作変数法）、暗に置かれている条件については補足資料や、各推定手法に関するコラムをご参照ください。 

 

一致性 

　前述のように潜在アウトカムを用いるRubin流の因果推論においては、因果効果は異なる介入レベルの潜在アウトカムの比較によって定義されます。ここで1つ重要なことがあります。それは、潜在アウトカムと観測されるアウトカムは異なる概念であるということです。あくまで潜在アウトカムとは、〇〇という介入を「仮に受けたとしたらどのような結果となるかというifの結果」であり、観測されるアウトカムは〇〇という介入を「実際に受けた場合の結果」です。つまり、潜在アウトカムを用いて定義される因果効果をデータ（観測される結果）から考えるためには、これら2つの異なるアウトカムをリンクさせる必要があります。 

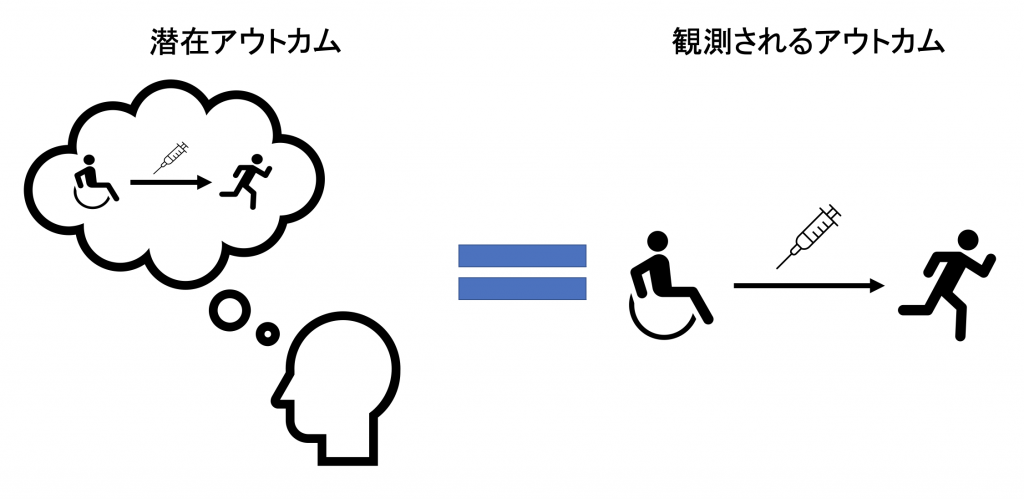
　そこで必要となるのが一致性 (consistency) と呼ばれる仮定です。一致性とは全ての個人に関して、ある介入A=aを受ける場合の潜在アウトカム Y^a が、実際にその介入を受けた場合に観測されるアウトカムYと一致することを意味します。例えば、介入Aを心臓移植の有無、アウトカムを介入から5日後の生存の有無としたとき、ある個人に対して想定される潜在アウトカムは、介入を受けない場合と受ける場合の結果であるY_i^a=0, Y_i^a=1の2つです。ここで仮に、被験者は実際に介入を受けたとします。すると、手術から5日後に観察された結果Yは、手術の前に考えた潜在アウトカム Y_i^a=1と同じであるというのが一致性が指す内容です。一見すると、大変当たり前のことを言っているように思われます。しかし、一致性は以下の2つの要素から構成され^※1、これらが成立しない場合には、潜在アウトカムと観測されるアウトカムが一致しない、もしくは後述の式の様な単純な関係とはならない場面があります。

• precise definition of the counterfactual outcomes 
• linkage of the counterfactual outcomes to the observed outcomes   

　1つ目の要素は、潜在アウトカムを構成する要素が十分に定義されているかどうかに関する項目です。ここまで心臓移植という介入の因果効果を考えるにあたり、介入を受ける場合の潜在アウトカム Y^a=1と受けない場合の潜在アウトカムY^a=0を比較しました。しかし、心臓移植を受けるといっても心臓移植を行う医師によって治療の効果は変わりうる可能性は十分考えられます（医師の手術の上手さが異なる）。このように単に介入を受けるといっても複数のバージョンがあり (multiple versions of treatment) 、かつ、それぞれの場合で介入による効果が異なる場合には、治療を受ける場合の潜在アウトカムを単にY_i^a=1とするのではなく、どのような治療を受けるのかといった情報まで含めて、潜在アウトカムの定義をする必要があります。precise definition of the counterfactual outcomesという項目はこのような、我々が想定する因果効果が定義する潜在アウトカムで十分に表現できているかに関した内容です。  

　2つ目の要素は、潜在アウトカムを定義する際に考えた介入と、実際に行われた介入が対応しているかどうかという部分に関する項目です。例えば、１つ目の要素を満たすように、「研究期間中体重が推移するとし研究開始時の体重を上回ったらカロリー制限を行う」という治療とそれに対応する潜在アウトカムが十分に定義されたとします。ここで問題なのは、仮に治療群に割り当てられたとした場合であっても、実際に治療が行われない場合があることです。しかし、解析を行うにあたっては各被験者が対照群と治療群のどちらの群に割り当てられたかの情報しかないため、因果効果を算出するためには、当初想定した潜在アウトカムが実際に観測されるアウトカムと同じである（群の割り当てと実際の介入が対応している）ということが必要になります。 linkage of the counterfactual outcomes to the observed outcomes はこのような当初の想定（潜在アウトカム）と現実のデータとの結びつきを意味しているものです。これらのより詳しい説明や、関連する仮定については補足資料をご参照ください。  

　また、一致性は数学的には次のように表現されます。 

If A_i = a, then Y_i^A = Y_i^a = Y_i  

特にAが二値であるとき、  

 Y_i = AY_i^a=1 + (1-A) Y_i^a=0  

とも表されます。しかし、「一致性」という用語は用いられる文脈によって意図する内容が異なるため注意が必要です。例えば、一般に統計学においては、あるパラメータの推定量の期待値がその真値と一致することを示す際に用いられています。そのため、因果推論における一致性であるということを強調するために、因果一致性 (causal consistency) と呼ぶ場合もあります。なお今後のコラムでは特に言及がない限り、一致性は成立するものとして議論を行います  

※1 Miguel A. Hernan, James M. Robinsによる    

 

因果推論の根源問題  

　前回のコラムで定義したように 、ある個人（集団）における因果効果は、その個人（集団全員）の潜在アウトカムの比較によって定義がされ、差のスケールで因果効果を考えた場合には、それぞれ次のように定義されました^※2。

• 個人iにおける因果効果：Y_i^a=1 - Y_i^a=0  
• 集団における平均因果効果：E[Y_i^a=1] - E[Y_i^a=0]  

　しかし、ある時点における介入は単一のレベルしかとることができず^※3、また一致性の仮定より、各介入レベルで定義される潜在アウトカムは、ある1つしか現実に観測がされず、それ以外の潜在アウトカムは現実には得られない結果（反事実）となります。すなわち、介入を受けない群に割り当てられた被験者に関してはY_i^a=1の情報が、介入を受ける群に割り当てられた被験者に関してはY_i^a=0の情報が得られず、欠測します^※4。 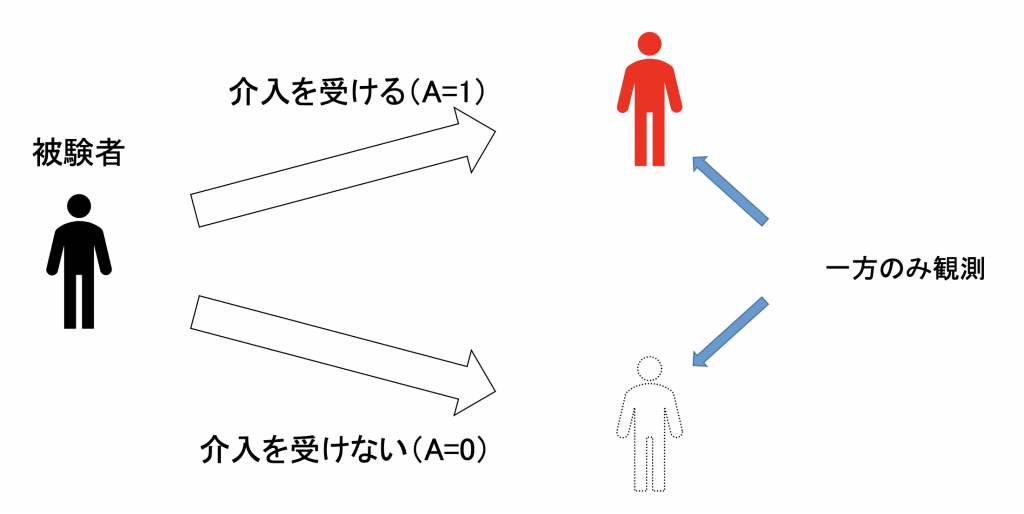　よって、個人の因果効果は定義することは可能であっても、その値をデータから算出することは現実的に不可能であり、この潜在アウトカムの欠測の問題はRubin流の因果推論の根源問題として知られています。では、平均因果効果も同様にその値を算出することはできないのでしょうか。結論から述べると平均因果効果は、一致性に加えて、次に紹介する交換可能性、正値性という仮定が成立する下では推定することが可能です。以降はこの平均因果効果について特に注目していきます。  

※2 本コラムでは、因果効果を一貫して差の（additiveな）スケールで考える
※3 今回の例であれば、介入のレベルは心臓移植を行う場合 (A=1) と行わない場合 (A=0) の2つであるが、また心臓移植と投薬といった複数の介入を同時に行う場合であっても同様の議論が可能
※4 介入の割り当ては完全に遵守されるものとする 

 

Causation versus association 

　集団における平均因果効果 E[Y_i^a=1] - E[Y_i^a=0] に着目するにあたり、その定義について改めて考えます。因果効果を示す指標は様々なものがありますが、その本質は前述のように、異なる介入レベルの潜在アウトカムの比較です。すなわち、介入が二値であるのならば、集団全員の「介入を受ける場合 (A=1) の潜在アウトカム」と「介入を受けない場合 (A=0) の潜在アウトカム」が必要です。  

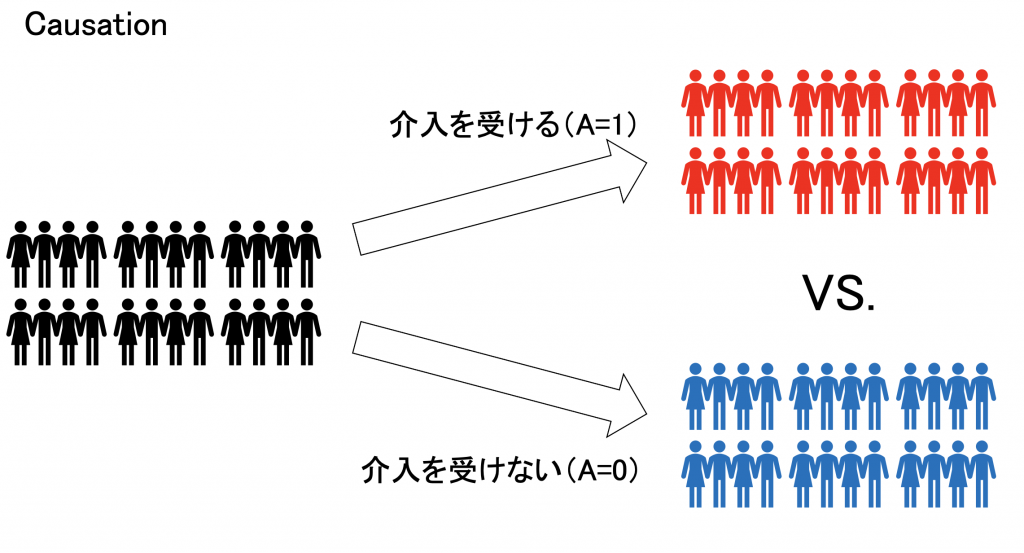
　しかし現実には、各個人は対照群 (A=0) と介入群 (A=1) に割り当てがされるので、一致性の仮定だけではデータから得られる結果は、集団全体の比較である因果関係 (causation) ではなく、介入を受けた人と受けなかった人という部分集団同士の比較結果 (association) でしかありません。

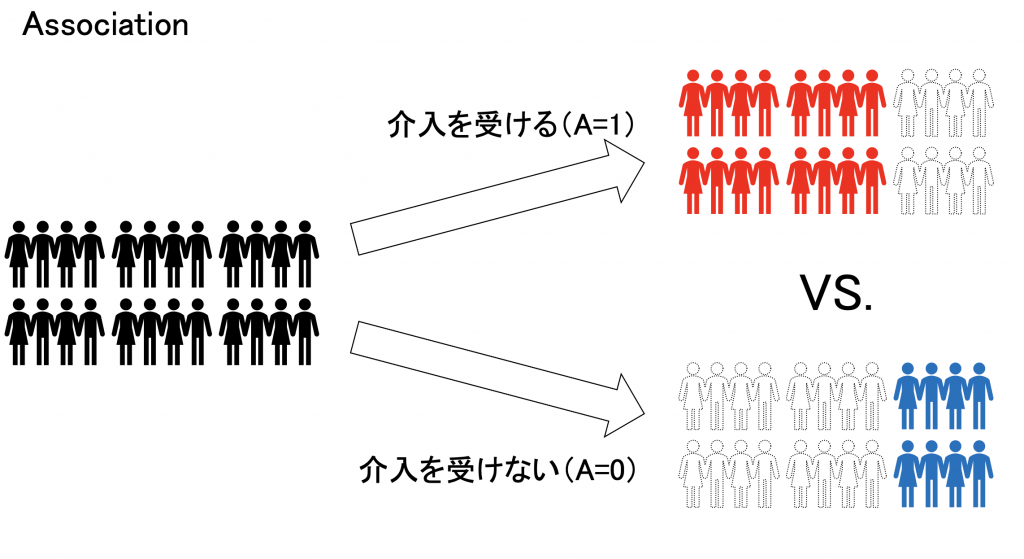
つまり、介入群と対照群で得られた結果が異なる（e.g. 介入群の方が症状が緩和した）場合であっても、それが介入による因果効果であるとは言い切れず、それぞれの集団の特性の違い（e.g. アウトカムを発生させにくい人が介入群に多く割り当てられている）である可能性もあります。もしかしたら、全員に介入を行わずとも同様の結果が得られていたかもしれません。この、どのような集団を比較しているかという違いが、相関関係が因果関係を意味しない (association is not causation) と言われる本質的な理由です。

 

 

交換可能性

　では、どのような状況であれば現実に観察される関係 (association) を因果関係 (causation) として見ることができるのでしょうか。ここで非常に重要となるのが、このセクションで紹介する交換可能性 (exchangeability) という仮定です^※5。次回のコラムのメインの内容にもなりますが、この交換可能性をどのようにして担保するかというのが因果関係を検討するにあたり最も重要となることの１つです。  交換可能性は介入が二値である場合には、次の2つを同時に意味します。 

1. 対照群 (A=0) 、介入群 (A=1) において潜在アウトカムY^a=0の分布は等しい
2. 対照群 (A=0) 、介入群 (A=1) において潜在アウトカムY^a=1の分布は等しい   

　つまり、交換可能性は、仮に各個人に対する介入群と対照群の割り当てを交換していた（逆にしていた）としても、同様の結果が得られるということを意味しています。医学的な言い方をするのであれば、例えば、いずれかの群に予後が悪い人（良い人）が偏っていないという状況です。また、想定される全ての部分集団 (A=0, 1) で得られるであろう結果が等しいので、当然それらは、集団全体での結果と一致します。 イメージとしては、下図のように介入群 (A=1) と対照群 (A=0) という部分集団で得られた結果を、それぞれ”集団全体が”治療を受けていた場合、受けなかった場合の結果とみなすというのが交換可能性が指す内容です。　

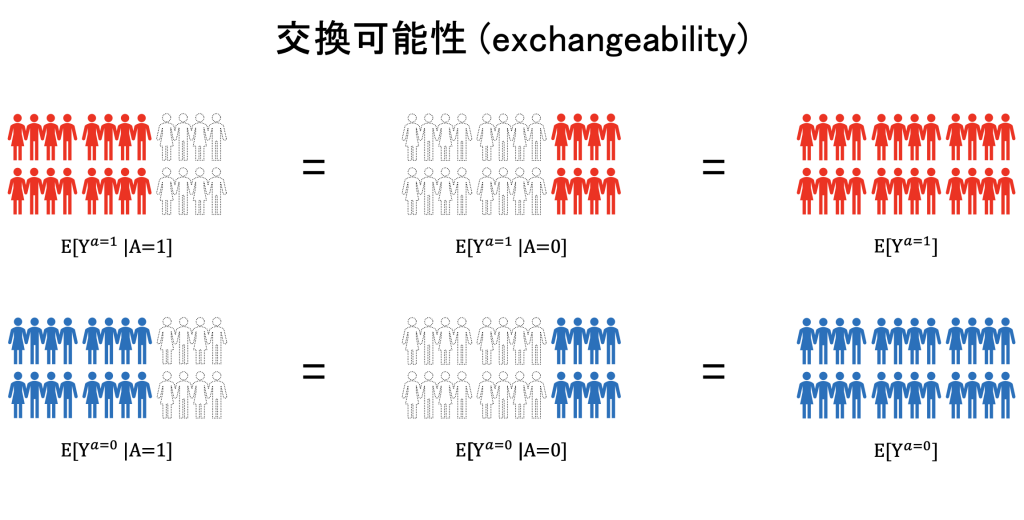
　そのため、部分集団の比較である相関関係を、集団全体の比較である因果関係として見ることが可能となり、数学的には次のように表されます。

E[Y^a=1|A=1] = E[Y^a=1|A=0] = E[Y^a=1]
E[Y^a=0|A=1] = E[Y^a=0|A=0] = E[Y^a=0] 

　特にアウトカムYがあるイベント（e.g. 手術から5日後の死亡）の有無といった二値アウトカムである場合には、以下のようにも書くことができます。 

Pr[Y^a=1=1|A=1] = Pr[Y^a=1=1|A=0] = Pr[Y^a=1=1]
Pr[Y^a=0=1|A=1] = Pr[Y^a=0=1|A=0] = Pr[Y^a=0=1] 

　上記の式をよく見ると、交換可能性の下では平均因果効果の定義に用いるE[Y^a=1],  E[Y^a=0]は、先ほどの一致性の仮定も加えることで、それぞれ実際のデータから計算可能な介入群における潜在アウトカム (E[Y^a=1|A=1]) と対照群における潜在アウトカムの期待値 (E[Y^a=0|A=0]) へと置き換えることが可能です。

　また交換可能性はより一般的に、数学的には次のように表現されます。 

Y^a ⊥ A for all a^※6   

ただ、実は単に交換可能性と言っても、厳密にはいくつか種類があります。この点については補足資料をご参照ください。  

※5 厳密には平均因果効果の算出のためには、補足資料で言及するように平均交換可能性で十分であり、特にアウトカムYが二値である場合には交換可能性と平均交換可能性は同義  
※6 ⊥は統計学上の独立を意味する 

 

正値性

　そして最後に紹介を行うのは正値性 (positivity) と呼ばれる仮定です。これは全ての個人に関して、解析時に考慮する変数Lで条件付けた場合に、ある介入 (A=a) を受ける確率が0~1の間に存在しているということを意味するものです。つまり、介入Aが治療を受けるか受けないかの二値変数であるとすると、必ず治療を受ける or 受けないといった個人は存在しないということを意味しています。数学的には以下のように表現されます。  

If Pr[L=l]≠0, 0 < Pr[A_i=a|L=l] < 1, for all l, i, a  

　この仮定が必要となるのは、集団における因果効果の定義より明らかです。なぜならば、例えばある介入の因果効果を考える集団において、絶対に治療を受けることがない個人 (Pr[A_i=a|L=l]=0) が存在するとなると、集団全員が治療を受ける場合E[Y_i^a=1]はそもそも定義できず、また平均因果効果E[Y_i^a=1] - E[Y_i^a=0]も考えることができません。  

　そのような例外的な場合を除外する意味合いで正値性の仮定は、因果推論を行う上で必要とされますが、交換可能性を成立させるために調整しなければならない変数が多い場合や、介入が複数の時点で行われるといった場面においては、正値性が成り立たない状況が発生することがあります。  

 

おわりに  

 　今回のコラムで紹介した3つの仮定の下では、潜在アウトカムを用いて定義された平均因果効果を現実のデータから考えることが可能です。中でも交換可能性は因果推論の文脈で最も議論に挙がる内容かと思います。実験研究における割り当てのランダム化や、様々な推定手法は、この交換可能性に関連する内容です。 次回のコラムではこういった、どのように交換可能性を満たすかについて、実験研究と観察研究に場合分けをしつつ考えていきます。また、しばしば因果推論で耳にする「交絡」というものについても紹介を行います。

 

補足 

参考 

• Hernán, M. A. and Robins, J. M. (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC. 
• 田中司朗. (2019). 医学のための因果推論の基礎概念,計量生物学 40(1), 35-62. 
• Imbens, G. W. and Rubin, D. B. (2015). Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction. Cambridge University Press. 
• Holland, P. W. (1986). Statistics and Causal Inference. Journal of the American Statistical Association, 81(396), 945-965. 
• Rubin, D. B. (1980). Randomization Analysis of Experimental Data: The Fisher Randomization Test Comment.  Journal of the American Statistical Association, 75(371), 591-193.
• Greenland S. and Robins, J. M. (2000). Epidemiology, Justice, and the Probability of Causation. Jurimetrix, 40(3), 321-340.
• VanderWeele, T. J. (2009). Concerning the consistency assumption in causal inference. Epidemiology, 20(6):880-883.