Blogs

Blogs

SASによる因果推論：PSMATCHプロシジャによる傾向スコアマッチング

0
By Topics | Analytics Students & Educators

はじめに

因果効果の推定手法の1つである傾向スコアマッチング、およびSASでの実装方法について紹介します。傾向スコアマッチングのSASでの実装にあたっては、本記事ではSAS/STAT 14.2（SAS 9.4）で追加されましたPSMATCHプロシジャを使用します。因果推論の基本的な枠組みや傾向スコア・傾向スコアマッチングの統計的理論については、詳しく解説を行いませんので、そちらに関心がある方は書籍等を参考にしていただければ幸いです。

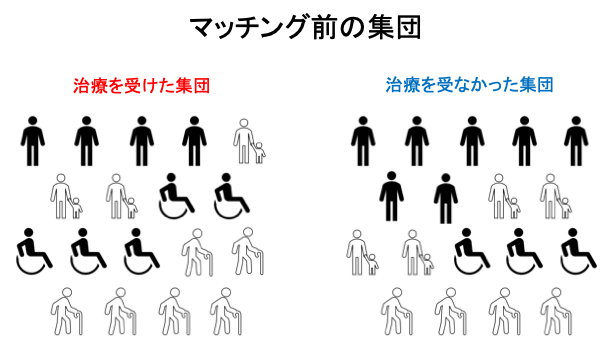
理想的なランダム化比較試験においては、ランダム化により治療群と対照群間で測定・未測定の交絡因子（confounders）の分布が期待的に等しくなるため、単純な群間比較によって治療（介入、曝露）の興味のあるアウトカムに対する効果を評価することが可能です。しかし、ランダム化が行われなかった実験研究や観察研究のデータから因果関係を見出そうとする場合には、一般に交絡（confounding）と呼ばれるという問題が生じます。これは簡単に述べると、治療群と対照群で集団の特性が異なることで2つの集団が比較可能ではない状況、治療群と対照群でのアウトカムの違いが治療だけではなく集団の特性の違いにも依存する状況を意味しています。つまり、ランダム化が行われなかった実験研究や観察研究のデータから因果効果を推定する際には、交絡を十分に制御した上で群間比較を行う必要があり、世間一般で因果効果の推定手法と呼ばれるものは、交絡を調整方法する方法だと認識していただいてよいかと思います。因果効果の推定手法は回帰や層別化、標準化など様々なものがありますが、本記事ではマッチング法に注目します。マッチング法は、治療群と対照群から類似した特徴を持つ被験者をペアとし（マッチングさせ）、マッチした対象集団において治療を受けた群と受けなかった群を比較するという方法です。

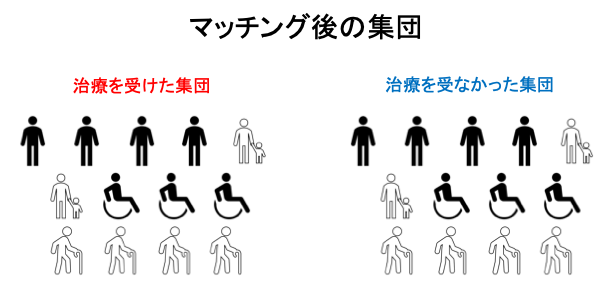
　ただ、一言にマッチング法と言っても複数の交絡因子（共変量）の情報をそのまま用いる「共変量マッチング」と、共変量の情報を傾向スコアという一次元の情報に落とし込んだ上でマッチングを行う「傾向スコアマッチング」という2つの方法に大きく分かれます。初学者にとっては前者の方がより直感的な方法かと思いますが、共変量が高次元である場合や変数のカテゴリ数が多い場合にはその実施が困難になります。そのような場合にしばしば用いられるのが後者の傾向スコアマッチングです。マッチングには、治療群と対照群の構成比率やマッチング方法など様々なオプションがありますが、傾向スコアの分布が同じ（治療群と対照群が交換可能）であるmatched populationを作成するというのが共通の考え方です。また、傾向スコアマッチングの実施手順は連続である単一の共変量を用いた共変量マッチングと同様であり、大きくは以下のような手順となります。

【傾向スコアマッチング法のステップ】

  1. 共変量の特定、測定
  2. 傾向スコアのモデル指定、傾向スコアの推定
  3. マッチングアルゴリズムの決定、マッチングの実施
  4. マッチングした対象者で構成された集団（matched population）における治療群と対照群での交絡因子の分布評価
  5. 4.で評価した共変量が不均衡である場合には2.に戻る
  6. 群間比較の実施
  7. 推定結果の解釈

 

記法と仮定

記法

以下の記法の下で傾向スコアマッチングに関する議論を行います。アルファベットの大文字は確率変数を、小文字はその実数値を意味するものとします。なお、以降でボ－ルド体としている場合は単一の変数ではなくベクトルであることを意味しているものとします。

  • A：二値の治療変数
  • Y：観察されるアウトカム
  • Ya：潜在アウトカム
  • X：共変量（一般にはベクトル）

仮定

本記事では以下の識別可能条件を仮定します。理想的なランダム化比較試験においては研究デザインによってその成立が認められますが、観察研究ではあくまで”仮定”となります。つまり、その成立を認めることが妥当であるかどうかの議論が別途必要となることにご注意ください。また、各条件の詳細や意図する内容については本記事では取り扱いませんので、他の記事や書籍等をご参照ください。

【識別可能条件 (Identifiability assumptions) 】

一致性 (consistency)

If Ai = a, then YiA = Yia = Yi 
特にAが二値であるとき、   Yi = AYia=1 + (1-A) Yia=0  

条件付き交換可能性 (conditional exchangeability)

Ya ⊥ A|X for all a of A and x of X

正値性 (positivity)

If f[X=x]≠0, then f[Ai=a|X=x]>0, for all x, i, a  

　なお、1つ目の仮定である一致性はしばしばSUTVA仮定に置き換わる場合があります。2つ目の仮定である条件付き交換可能性は未測定の交絡因子がないこと (no unmeasured confounders) と同義です。

 

傾向スコア

傾向スコア (propensity score) π(X)とは、共変量ベクトルXで条件付けた場合の治療を受ける確率です。すなわち

π(x) = Pr[A=1|X=x]

であり、傾向スコアの値が0に近い個人は治療を受ける確率が低いことを、1に近い個人は治療を受ける確率が高いことを意味しています。傾向スコアの持つ1つ目の重要な性質としては、バランス性が挙げられます。すなわち、傾向スコアとは以下を満たすバランシングスコアb(X)の1つです。

A⊥X|b(X)

　このバランス性は、同じ傾向スコアの値を持つ集団においては共変量Xと治療Aが独立であること、同じ傾向スコアの値を持つ治療を受けた集団と受けなかった集団の共変量分布が同じであることを意味しています。余談ですが、共変量X自体もバランシングスコアに該当します。また、傾向スコアはスカラーとなることから最も粗いバランシングスコアと言われます。

そして、傾向スコアの持つ2つ目の重要な性質として以下の独立性が挙げられます。これは識別可能条件の1つである条件付き交換可能性と傾向スコアのバランス性より導かれます。

Ya⊥A|π(X)

　真の傾向スコアが得られているという状況は、ランダム化比較試験や一部のシミュレーション実験などに限定され、実際のデータ解析を行う場合には基本的にその値を推定する必要があります。すべての交絡因子が特定・測定され、その数が少数かつ値のカテゴリ数が少ない場合には共変量の層内の治療割合によって傾向スコアの値を推定することが可能ですが、一般には特定のモデルを用いて推定を行います。稀にプロビット回帰モデルや近年では機械学習的手法が傾向スコアの推定に用いられますが、最も頻用されるのはロジスティック回帰モデルです。SASのPSMATCHプロシジャでは、データセットに傾向スコアの値が既に含まれている場合にはPSDATAステートメントでその指定を、含まれていない場合にはPSMODELステートメントで想定するロジスティック回帰モデルの指定を行う必要があります。ロジスティック回帰モデル以外で推定した傾向スコアの値を使用したい場合には、ロジスティック回帰モデル以外で推定した値をデータセットに加えた上でその変数列をPSDATAステートメントで指定する必要があります。なお、傾向スコアマッチングでは傾向スコアを推定するため、妥当な推定量を得るためには識別可能条件の成立の他に傾向スコアのモデルが正しく特定されていることが必要です。

 

マッチングにおける代表的な要素

キャリパー (caliper)

ある2人の被験者が正確に同じ傾向スコアの値を持つことは非現実的であるため、ある程度傾向スコアが異なる個人をペアとすることが現実的な対応となります。このペアを作成するにあたり許容する最大の幅がキャリパー (caliper) です。より大きなキャリパーを認めることはマッチングの実現可能性を高めますが、一方でより傾向スコアの値が異なる個人をペアとすることを意味しているため、結果として残差交絡がより大きくなる可能性があります。このキャリパーの基準としては、傾向スコアのロジット変換した値の標準偏差に0.25をかけたものがRosenbaum and Rubin (1985) によって、0.20をかけたものがAustin (2011) によって推奨されています。なお、後述するPSMATCHプロシジャでのデフォルト設定は0.25です。

マッチング方法

SASのPSMATCHプロシジャで指定可能な治療群と対照群の被験者のマッチング方法・ペアの作成方法は以下のように大きく3つ分けられます。PSMATCHプロシジャではMATCHステートメントで指定します。

  • 貪欲最近傍マッチング (Greedy Nearest Neighbor Matching)
    ある治療群の被験者1名に対して最も近い傾向スコアの値を持つ対照群の被験者をペアとする方法。復元抽出を認めず（非復元抽出）、治療群の被験者1名に対して1名以上をペアとする。また、どの傾向スコアの値からマッチングを行うかについては昇順・降順・ランダムの3つから選択。
  • 復元マッチング (Replacement Matching)
    復元抽出を許容し、ある治療群の被験者1名に対して最も近い傾向スコアの値を持つ対照群の被験者1名以上をペアとする方法。
  • 最適マッチング (Optimal Matching)
    復元抽出を認めず、ペアの傾向スコアの差の絶対値の和を最小化するようにマッチングさせる方法。

最適マッチングはさらに以下の3つの方法に分けられます。

  • 固定比マッチング (Fixed Ratio Matching)
    ある治療群の被験者1名に対してマッチングさせる対照群の人数を指定（固定）する方法。
  • 変動比マッチング (Variable Ratio Matching)
    ある治療群の被験者1名に対してマッチングさせる対照群の人数の上限を指定（固定）する方法。被験者によってペアの人数は異なってOK。
  • フルマッチング (Full Matching)
    ある治療群の被験者1名に対して1名以上の対照群の被験者をマッチングさせ、かつある対照群の被験者1名に対して1名以上の治療群の被験者をマッチングさせる方法。他のマッチング方法ではmatched populationに含まれない被験者が一般に存在するが、フルマッチングでは全員が含まれる。

共変量の群間差

傾向スコアπ(X)の持つ重要な性質としてバランス性A⊥X|π(X)を紹介しました。傾向スコアモデルが正しく特定されているのであれば、matched populationにおける治療群と対照群では、すべての共変量分布が等しく分布しているはずであり、もしそうでないのであれば指定した傾向スコアモデルを再考する必要があります。分布の群間での同等性を評価する指標として標準化差が広く用いられており、その基準としてはRubin (2001) やStuart (2010) によって25%が、Normand et al. (2001), Mamdani et al. (2005) やAustin (2009) によって10％が推奨されています。PSMATCHプロシジャではASSESSステートメントを用いて評価します。

 

推定値の解釈について

傾向スコアマッチングは、その実施が比較的容易であるため統計学・因果推論のライトユーザーに好まれる傾向がありますが、推定値の解釈が困難になる場面があります。治療群と対照群での傾向スコアの分布が共通する範囲は共通サポート (common support) と呼ばれますが、この傾向スコアの分布の群間での関係によって、その解釈は異なります。まず、additiveなスケールでのいくつかの代表的な因果効果の定義を紹介します。

【ATE; average treatment effect】

E[Ya=1] - E[Ya=0]

【ATT; average treatment effect on treated】

E[Ya=1|A=1] - E[Ya=0|A=1]

【ATC; average treatment effect on controlled】

E[Ya=1|A=0] - E[Ya=0|A=0]

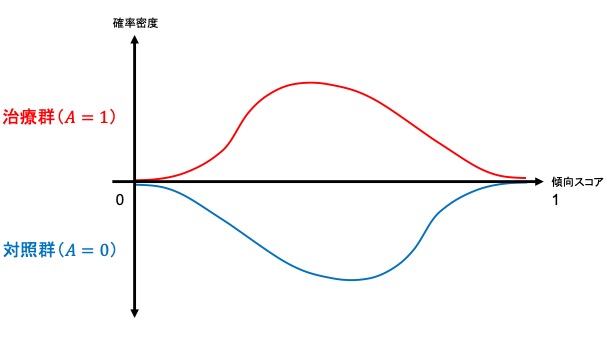
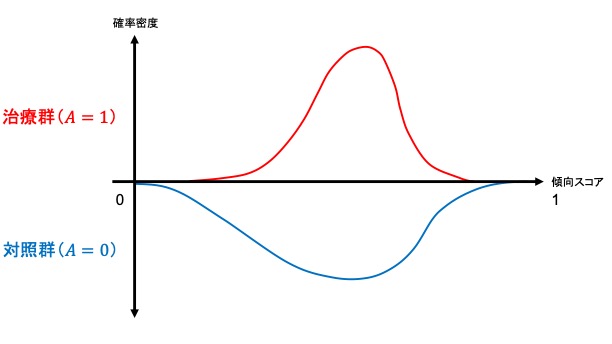
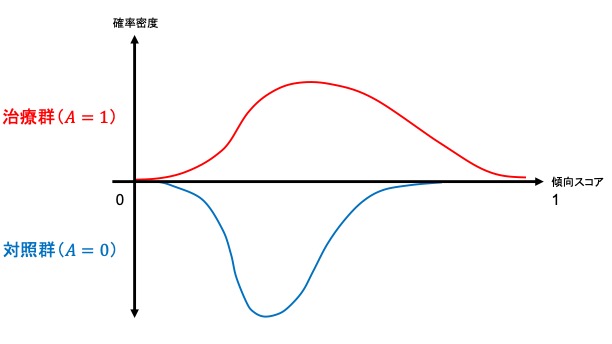
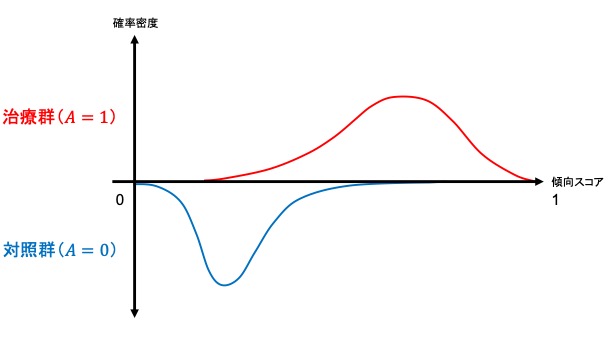
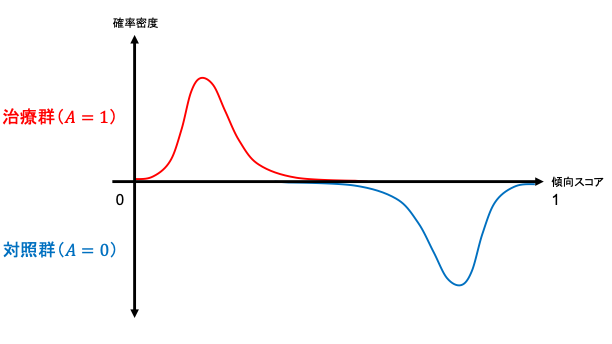
　集団全体がもしも治療を受けなかった場合と比較して治療を受けた場合にはどの程度アウトカムの値が異なるかというのを示したのがATEであるのに対し、ATT, ATCはそれぞれ実際に治療を受けた集団、受けなかった集団での平均治療（因果）効果にあたります。すなわち、ATT, ATCは局所平均治療効果 (LATE; local average treatment effect) です。ここで両群の傾向スコアの傾向スコアの分布（範囲）によって、マッチング方法にもよりますが、推定可能な因果効果が異なります。以下が簡単なイメージです。

  • 両群の分布の範囲が同じ→平均因果効果 (ATE) を推定可能

  • 治療群の分布の範囲が対照群の分布の範囲の一部→治療群における平均因果効果 (ATT) を推定可能

  • 対照群の分布の範囲が治療群の分布の範囲の一部→対照群における平均因果効果 (ATC) を推定可能

  • 両群の分布の重なりが一部、完全分離→解釈・群間比較が困難

 

PSMATCHプロシジャ

PSMATCHプロシジャで傾向スコアマッチングを行う場合の基本的なステートメントは以下の通りです。本記事ではPSMATCHプロシジャで指定可能なステートメントのうち、傾向スコアマッチング特有のステートメントについてのみ紹介します。各ステートメントの詳細については、こちらのドキュメントをご参照ください。

PROC PSMATCH data=<使用するデータセット名>;
	ASESS <郡間で評価をする変数に関する指定>;
	CLASS <カテゴリ変数>;
	MATCH <マッチング方法・キャリパーの指定など>;
	PSMODEL 治療変数<(treated='level')> = <説明変数>;
	OUTPUT <出力データに関するオプション>;
run;

 

PSMARCHステートメント

PSMATCHステートメントには、使用するデータセットを指定するDATAオプションと、マッチングに使用する傾向スコアの区間範囲に関するREGIONオプションがあります。MATCHステートメントが記載されている場合のデフォルトはREGION=TREATED、記載されていない場合のデフォルトはREGION=ALLOBSとなっています。

ASSESSステートメント

ASSESSステートメントでは、マッチング前後での治療群と対照群においてその分布を評価したい共変量の指定を行います。構文としては以下です。

ASSESS   <LPS> <PS> <VAR=(var-list)>  </assess-options>

【基本的なオプション】

  • LPS
    記載した場合には、治療群と対照群のロジット変換後の傾向スコアを評価。
  • PS
    記載した場合には、治療群と対照群の傾向スコアを評価。
  • VAR
    治療群と対照群において分布の評価を行いたい変数を指定（二値or連続値に限定）。

【それ以外のオプション】

  • PLOTS=
    標準化差などのプロットを行いたいものを指定。
  • STDDIFFDIV=
    POOLEDもしくはTREATEDを指定可能（デフォルトはPOOLED）。標準化を行う際の除数（分母）に関する指定オプション。
  • VARINFO
    記載した場合には治療群と対照群における変数情報のテーブルを表示。
  • WEIGHT=
    用いる重みを指定。MATCHWGT治療群の被験者1名に対して複数の対照群の被験者がマッチングさせ、最終的な推定目標がATTである場合には特にMATCHWGTが関係する。

MATCHステートメント

MATCHステートメントでは、前述した用いるマッチング方法やキャリパーの基準等を指定します。

【オプション】

  • CALIPER=
    用いるキャリパーの基準を指定（デフォルトは0.25）。さらにMULTとSTATに関するオプションあり。
  • EXACT=
    正確にマッチングさせる変数を指定。広義の傾向スコアマッチングのようにキャリパーを持たせるのではなく、厳密に同じ値（e.g., 性別が同じ）である必要あり。
  • METHOD=
    5つの方法（上記のマッチング方法を参照）のいずれかを指定（デフォルトはOPTIMAL）。マッチング方法だけでなく、治療群と対照群の構成比（治療群1名に対し何名をマッチチングさせるか）も指定可能。
  • STAT=
    マッチング後の治療群と対照群において比較を行う統計量を指定。

PSMODELステートメント

PSMODELステートメントでは、傾向スコアの推定を行う際に用いるロジスティック回帰モデルのモデル式を指定します。構文としては以下です。

PSDMODEL treatvar<(treated='level')> = <effects></WEIGHT=weight>;

ここで治療変数 (treatvar) は二値変数である必要があり、治療を受けたことを示す値を指定する必要があります（e.g., treated='1'）。WEIGHTオプションは、IPW推定を行う際に主に傾向スコアの逆数として定義される重みのことを意味しているのではなく、ロジスティック回帰モデルをフィッティングさせる際に用いる各被験者の重みをその値として持つ変数を指定します。このオプションは一般的な傾向スコアの推定では記載しませんが、あるオブザベーションが何かしらの理由で全く同じ共変量情報を持つといった限定的な状況において用います。なお、傾向スコアの推定を行わない（i.e., PSMODELステートメントを記載しない）場合には、PSDATAステートメントを代わりに記載して読み込んだデータセットに含まれる傾向スコアを示す変数を指定する必要があります。

 

実装例（SmokingWeight）

PSMATCHプロシジャによる傾向スコアマッチングの実装例として、以下の動画で紹介がされている例をこちらの資料を参考にしつつ、一部改変して紹介します。

video.sas.com

データ説明 / 傾向スコアマッチングの設定

使用するデータセットは、Hernán and Robins (2019) で紹介がされているNHANES I Epidemiologic Follow-Up Studyのデータの一部です。この研究では1971年（ベースライン）とその10年後（フォローアップ終了時点）に実施された健康診断において、以下に示すような医学的・行動学的な情報が測定されています。

  • Activity：日常的な活動レベル (0, 1, 2)
  • Age：1971年時点での年齢
  • BaseWeight：ベースラインでの体重 (kg)
  • Change：ベースラインと10年後の体重変化 (kg)
  • Education：教育レベル (0, 1, 2, 3, 4, 5)
  • Exercise：定期的に行われるレクリエーションでの運動量 (0, 1, 2)
  • PerDay：1971年の1日に吸うたばこの本数
  • Quit：調査期間中の禁煙 (1: Yes, 0: otherwise)
  • Race：人種 (0: white, 1: otherwise)
  • Sex：性別 (0: male, 1: female)
  • Weight：フォローアップ終了時点の体重 (kg)
  • YearsSmoke：喫煙年数

後述する傾向スコアマッチングの目的や変数の設定、マッチング法は以下の通りです。

  • 目的：「禁煙を行った集団における禁煙の体重変化に与える平均因果効果 (ATT) の推定」
  • 治療変数：Quit
  • 興味のあるアウトカム：Change
  • 交絡因子：Sex, Age, Education, Exercise, Activity, YearsSmoke, PerDay
  • 使用するマッチング方法：

解析結果

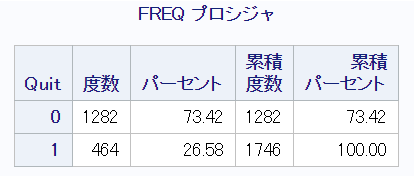
用いるNHANES I Epidemiologic Follow-Up Studyのデータセットにおける治療群 (Quit=1) と対照群 (Quit=0) の人数は、それぞれ464名、1282名（合計1746名）です。

このうち欠測があるオブザベーションを削除した後の治療群 (Quit=1) と対照群 (Quit=0) の人数は、それぞれ403名、1163名（合計1566名）です。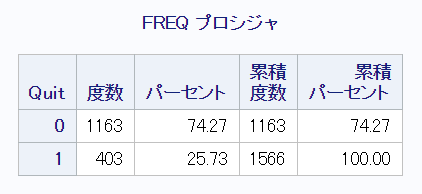

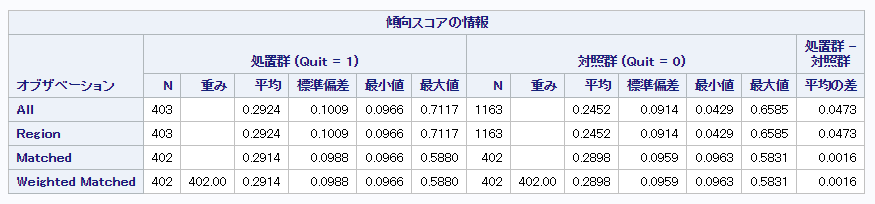
以降では、この集団に傾向スコアマッチングを行います。実際には、欠測の数やその理由によって欠測に対する対応が異なりますが、傾向スコアマッチングのSASでの実装方法を紹介することが本記事の目的ですのでご容赦ください。今回用いるマッチングの方法は、治療群と対照群の比率を1:1、傾向スコアのロジット変換した値の標準偏差に0.25をかけたものをキャリパーとした貪欲最近傍マッチングです。マッチング後の結果が以下になります。なお、欠測対応後の治療群403名中1名がマッチング不可となりましたが、軽微な影響であるとして今回は無視します。

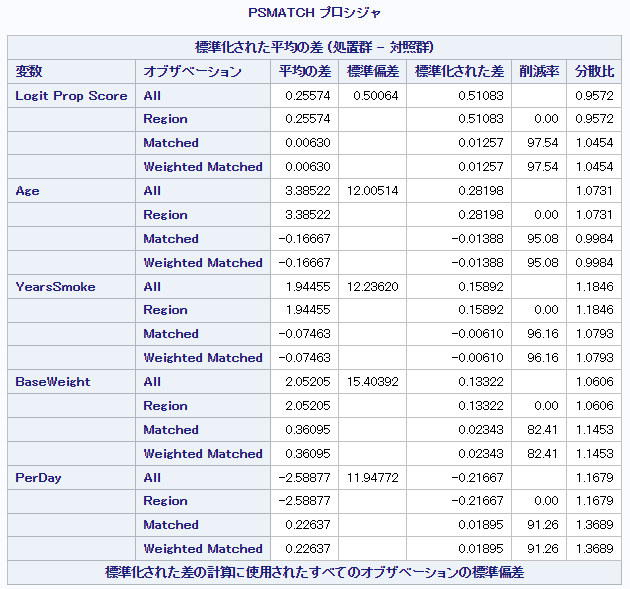
次に一部の共変量 (Sex, Age, YearsSmoke, PerDay) の標準化差を確認します。

【実数値】

【プロット】

青く塗られている部分が25%に該当する範囲となっています。

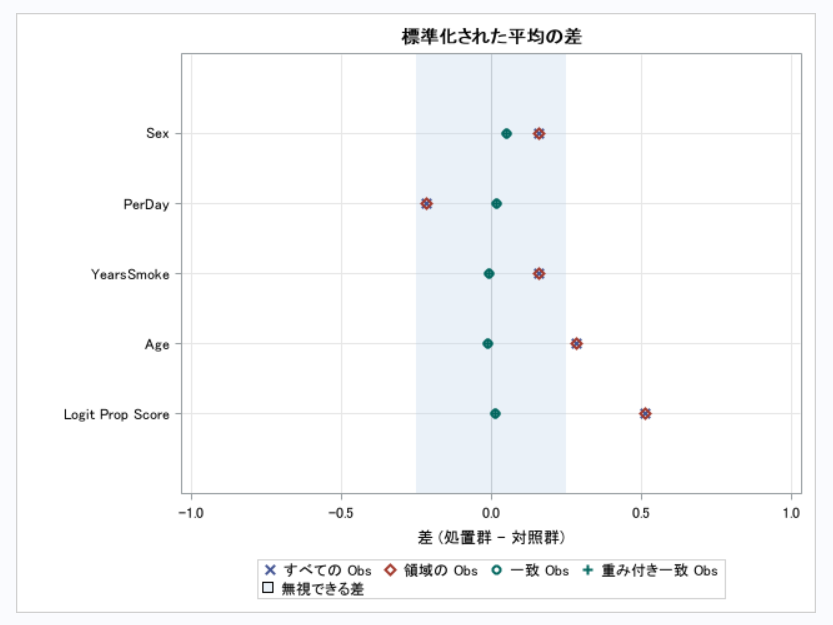
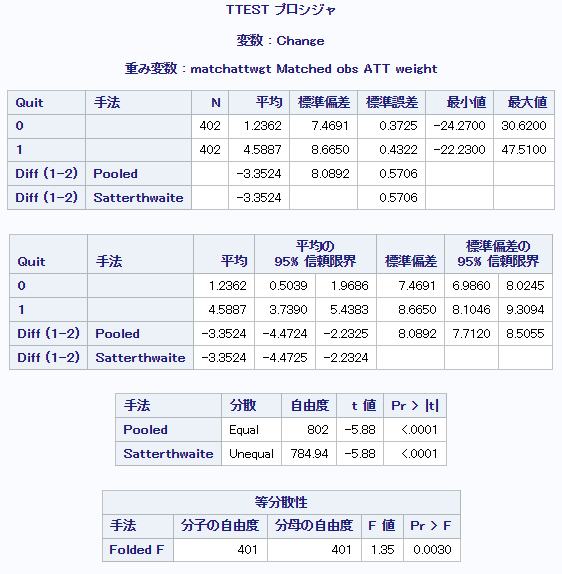
上図から明らかなように、標準化差が25％未満となっていることから共変量の分布が群間で等しい、傾向スコアモデルが妥当なものであるとします（より厳しい10%を基準として用いても同様）。なお、各変数のボックスプロットも出力可能ですが記載量の都合で省略します。最後にmatched populationに対してt検定を行います。以下に示すように、今回の例ではATTは-3.3524, 95％信頼区間は[-4.4724, -2.2325]と推定されました。つまり、禁煙を行った集団 (A=1) においては、もしも禁煙を行わなかった場合と比較して禁煙を行うと体重が3.3524kg減少すると推定されました。

 

サンプルコード

/*Create a dataset*/
/*See https://documentation.sas.com/doc/en/statug/v_005/statug_code_ctrtex1.htm*/
 
proc freq data=SmokingWeight;
	table Quit;
run;
 
/*Delete subjects with NULL*/
data SmokingWeight;
	set SmokingWeight;
	if nmiss(of _numeric_) > 0 then delete;
	id = _N_;
run;
proc freq data=SmokingWeight;
	table Quit;
run;
 
ods graphics on;
/* Conduct a PS matching*/
proc psmatch data=SmokingWeight region=allobs;
	class Sex Race Education Exercise Activity Quit ;
	psmodel Quit(Treated='1') = Sex Age Education Exercise Activity YearsSmoke PerDay;
	match method=greedy(k=1 order=descending) distance=lps caliper=0.25;
	assess lps var=(Sex Age YearsSmoke PerDay) / plots=(CDFPlot BoxPlot StdDiff);
	output out(obs=all)= SmokeMatched1 weight=matchattwgt matchid=MID;
run;
 
/*Estmate ATT*/
data SmokeAnalysis;
	merge SmokeMatched1 SmokingWeight;
	by id;
run;
proc ttest data=SmokeAnalysis;
	class Quit;
	var Change;
	weight matchattwgt;
run;
ods graphics off;
Tags JPN Academic 統計的因果推論
Share

About Author


Academic Staff

公共ソリューショングループ / 東京医科大学大学院医学研究科 生物統計学（Biostatistics）と統計的因果推論（Causal Inference）を専攻しています。お気軽にご連絡ください。

Leave A Reply

Back to Top